Dos partículas unidas por un oscilador armónico
De Laplace
1 Enunciado
Supongamos dos partículas de la misma masa m unidas por un resorte de constante k y longitud natural nula. Inicialmente ambas masas se encuentran en el mismo punto; y se le comunica a la partícula 2 una velocidad v0 alejándola de la primera, mientras que la partícula 1 se encuentra inicialmente en reposo. ¿Cuál es el movimiento subsiguiente de ambas partículas?
2 Solución
Una vez que las dos masas se ponen en marcha, todas las fuerzas del sistema son internas (elásticas, debidas a la acción del muelle). las ecuaciones de movimiento para ambas partículas. Además, al estar dirigidas en la dirección de la recta que une las dos partículas, que es la misma de la velocidad inicial, resulta un movimiento unidimensional de ambas partículas.
Las ecuaciones de movimiento para ambas partículas son
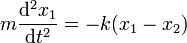
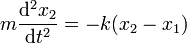
por ser de la misma masa, el centro de masas estará siempre en el punto medio de ambas partículas
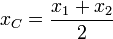
La ecuación de movimiento para el centro de masas es
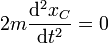
por lo que el centro de masas sigue un movimiento uniforme

siendo su posición y su velocidad iniciales
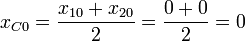
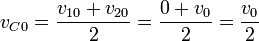
por lo que el centro de masas se mueve como

Para obtener el movimiento de cada partícula por separado, consideramos la posición relativa al centro de masas

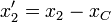
Cumpliéndose que
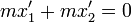

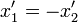
También se verifica que
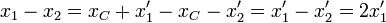
La ecuación de movimiento para x'1 es
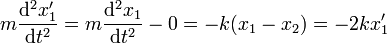
Por tanto, la posición relativa describe un movimiento armónico simple

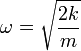
La amplitud y la fase la obtenemos de las condiciones iniciales
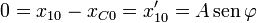
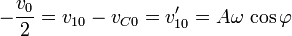
por lo que
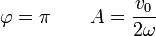
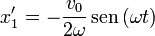
La posición de cada una de las partículas es entonces

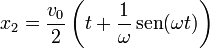
y la velocidad
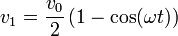
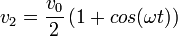
La energía cinética de este sistema no permanece constante, sino que oscila en el tiempo
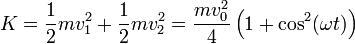
La energía cinética asociada al movimiento del centro de masas es
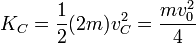
por lo que la parte de la energía cinética asociada al movimiento alrededor del centro de masas es
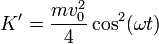
Esta energía es la debida al movimiento de oscilación armónica que describen las partículas en torno al CM.






