Propulsión a reacción
De Laplace
Contenido |
1 Enunciado
Un cohete a reacción se impulsa en el espacio emitiendo gases a cierta velocidad en el sentido opuesto a su propio movimiento. Sea un cohete que tiene una masa M0 y lleva una carga inicial de combustible m0. Este combustible es expulsado a ritmo constante 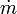 con una velocidad constante respecto a la nave, v0. Si la nave parte del reposo, ¿cuál será su velocidad cuando se le agote el combustible?
con una velocidad constante respecto a la nave, v0. Si la nave parte del reposo, ¿cuál será su velocidad cuando se le agote el combustible?
2 Solución extendida
Si el cohete se mueve por el espacio libre de fuerzas externas, la cantidad de movimiento del sistema debe conservarse en todo momento. Pero, dado que los gases expulsados se llevan una cierta cantidad de movimiento el resultado es que la cantidad de movimiento del cohete también varía.
Para determinar la velocidad como función del tiempo, establecemos la conservación de la masa y de la cantidad de movimiento entre un instante t y un instante siguiente t + dt.
Si suponemos que los gases son expulsados siempre en la misma dirección en la que se mueve el cohete (aunque si deseara maniobrar debería expulsarlos en una dirección diferente) el problema es unidimensional, por lo que podemos usar cantidades escalares.
En el instante t la cantidad de movimiento del cohete más el combustible que lleva en ese momento es
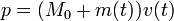
En el instante t + dt la masa de la nave más combustible pasa a ser
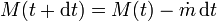
mientras que su velocidad pasa a ser
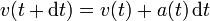
La cantidad de gas expulsada es
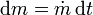
y la velocidad con la que se mueve este gas no es v0, ya que esta es la velocidad con la que sale expulsado respecto a la nave. La velocidad del gas, para un observador exterior es
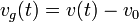
Aplicando ahora la ley de conservación de la cantidad de movimiento queda
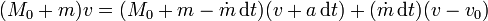
Desarrollando y eliminado los términos que quedan a ambos lados resulta, tras simplificar
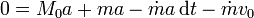
El término proporcional a dt es despreciable, con lo que llegamos finalmente a la relación
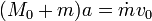
Aquí m no es una constante, sino que
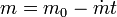
Para obtener la velocidad como función del tiempo, despejamos la aceleración
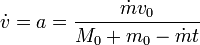
Integrando entre t = 0 y 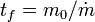 (cuando m se hace 0) obtenemos la velocidad final
(cuando m se hace 0) obtenemos la velocidad final
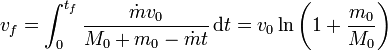
Esta fórmula hay que corregirla para el caso de que se alcancen grandes velocidades o en lugar de gases se emita energía pura (como luz), en cuyo caso hay que usar cálculos relativistas.
3 Solución abreviada
Podemos resolver este mismo problema, usando los mismos principios, pero sin necesidad de introducir el tiempo como variable.
la ecuación básica es que en dos instantes sucesivos la cantidad de movimiento del sistema nave+gas expulsado es la misma, y por tanto
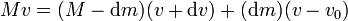
siendo M la masa total de la nave más el combustible que le que quede en un instante dado y dm el diferencial de masa de gas expulsado.
Despejando e igualando queda
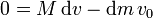
donde hemos despreciado el término 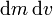 que es mucho más pequeño que los demás. Equivalentemente
que es mucho más pequeño que los demás. Equivalentemente
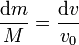
La cantidad de masa expulsada es igual a lo que disminuye la masa del cohete, por lo que
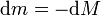
esto es

Integrando cada miembro
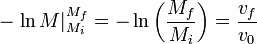
La masa inicial es la del cohete más el combustible, mientras que la del final es solo la del cohete, por lo que obtenemos finalmente
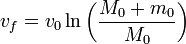
Obsérvese que el resultado realmente no depende de que la masa se expulse a ritmo constante.
4 Solución aun más abreviada
Podemos llegar a este resultado de forma aun más corta empleando el sistema centro de masas. Puesto que en un instante dado estamos considerando la nave y el combustible que lleva dentro, la velocidad del centro de masas coincide con la de la nave en ese instante. Por tanto, antes de que expulse la masa dm de gases, la velocidad de la nave en el sistema CM es cero.
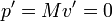
Después de que expulse estos gases, la nave ha adquirido una velocidad dv, mientras los gases tienen una velocidad − v0, por lo que la conservación de la cantidad de movimiento implica
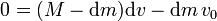
y a partir de aquí el problema sigue como en la sección anterior.
5 Combustible necesario
Si deseamos colocar una cierta cantidad de carga útil a una cierta velocidad, la cantidad de combustible necesaria se obtiene depejando

Este crecimiento exponencial con la velocidad hace que sea muy importante optimizar la masa del cohete para reducir el combustible necesario. Por ello, los cohetes constan de fases, que se van desprendiendo a medida que dejan de ser necesarias.





