Colisión de dos péndulos

De Laplace

1 Enunciado

Se tienen dos péndulos ideales con barras rígidas de la misma longitud L y masa nula, que cuelgan del mismo punto O. Las masas sujetas a los extremos de los hilos son respectivamente m₁ y m₂. La masa m₁ es elevada a una altura h₁ y se suelta desde el reposo, colisionando con la masa m₂ que se encuentra en el punto más bajo.

Suponiendo que la colisión es elástica, determina la altura a la que sube cada masa tras la colisión. Distingue los casos m₁ > m₂, m₁ = m₂ y m₁ < m₂.

¿Qué condiciones deben cumplirse para conseguir que la masa m₂ gire y llegue hasta arriba del todo?

2 Ecuaciones generales

La dinámica de este sistema es simple: la masa m₁ desciende y golpea horizontalmente a la masa m₂. Como resultado de la colisión, ambas adquieren una nueva velocidad, lo que las impulsa hacia arriba, ascendiendo hasta una cierta altura máxima. En ciertos casos, como veremos, una de ellas puede llegar a dar la vuelta completa.

En la colisión, por ser elástica, se conservan tanto la energía como el momento cinético. La conservación del momento cinético equivale en este caso, como en el del péndulo balístico, a la conservación de la cantidad de movimiento.

Al ser las velocidades inmediatamente antes y después de la colisión puramente horizontales, podemos escribir la conservación de la cantidad de movimiento en forma escalar, considerando solo la componente horizontal:

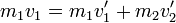
La conservación de la energía cinética nos da

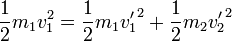
Operando en estas ecuaciónes, como en el problema de las colisiones de dos partículas obtenemos

        

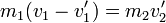
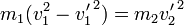
Dividiendo la segunda por la primera llegamos al sistema lineal

        

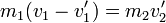
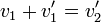
cuya solución es

        

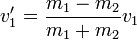
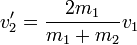
¿Cómo se relacionan estas velocidades con las alturas que alcanzan los péndulos? Aplicamos la conservación de la energía mecánica a cada uno de ellos. Toda la energía cinética en el punto inferior se convierte en energía potencial en el punto más alto, por lo que

          ,    

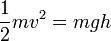
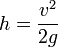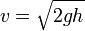
Con esto ya tenemos resuelto el problema. Ya solo queda analizar los diferentes casos

3 Caso m₁ > m₂

Cuando el proyectil tiene mayor masa que el blanco, m₁ > m₂, las velocidades resultantes tienen el mismo signo que la inicial

    ,    

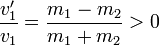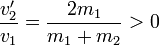
Esto quiere decir que las dos masas ascienden hacia el mismo lado, subiendo la segunda más que la primera, ya que v'₂ > v'₁. La altura a la que sube cada una es

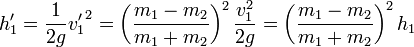
y del mismo modo

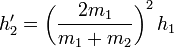
4 Caso m₁ = m₂

En el caso particular de que las dos masas sean iguales la solución anterior se simplifica, ya que en ese caso v'₁ = 0 lo cual quiere decir que la masa m₁ se queda “clavada” en el punto más bajo y la otra sube hasta exactamente la misma altura que la inicial

    ,    

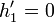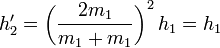
5 Caso m₁ < m₂

En el caso de que el proyectil sea más ligero que el blanco, el proyectil retrocede tras la colisión, mientras que el blanco se mueve en el sentido original

    ,    

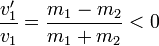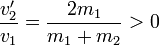
esto quiere decir que cada una de las partículas asciende a una cierta altura, una para cada lado. la fórmula para la altura es exactamente la misma que antes.

    ,    

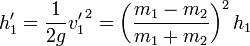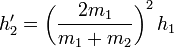
En realidad, en los tres casos valen las mismas fórmulas. Con lo único que hay que tener cuidado es hacia qué lado ascienden tras la colisión.

6 Condición para llegar al extremo superior

Para que la masa m₂ llegue al punto más alto, de altura 2L debe cumplirse en primer lugar que m₂ < m₁ si el blanco fuera más pesado que el proyectil nunca podría subir a mayor altura que la inicial (matemáticamente, porque 2m₁ / (m₁ + m₂) < 1.

Suponiendo que m₂ < m₁ la condición es que

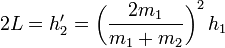
lo que nos establece una altura mínima desde la cual debe lanzarse el proyectil

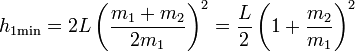
En el caso límite 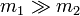esta altura mínima tiende a L / 2, lo que quiere decir que el péndulo debe formar un ángulo inicial mínimo de 60° con la vertical. Por debajo de ese ángulo nunca conseguiremos que m₂ llegue hasta arriba, por muy grande que sea m₁. Por encima, dependerá de la relación entre las masas el que lo consigamos o no.