Problemas de conceptos fundamentales de Termodinámica (GIA)
De Laplace
Contenido |
1 Volumen y número de moléculas de un gas
Utilizando la ecuación de estado de los gases ideales, responde a las siguientes preguntas
- ¿Qué volumen ocupa un mol de gas en condiciones estándar?
- ¿Cuantas moléculas hay en
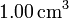de gas ideal a una temperatura de 
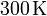y a un presión de 
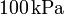? ¿Y si la presión es de 
?.
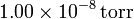2 Procesos de un gas ideal en diagramas
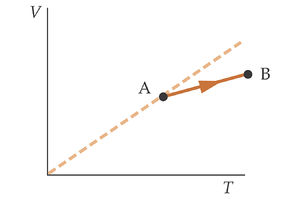
La figura de la izquierda muestra en un diagrama V-T un proceso realizado por una cantidad fija de un gas ideal. El gas pasa del estado A al estado B. ¿Qué ocurre con la presión del gas?
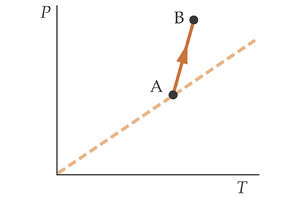
En la segunda gráfica tenemos otro proceso descrito por el gas en un diagrama P-T. ¿Qué ocurre en este caso con el volumen del gas?
3 Gas que escapa de un tanque a temperatura constante
Un manómetro sumergido en un tanque registra la presión nanométrica, que es la diferencia entre la presión interior y exterior (esta última es la presión atmosférica). Cuando el tanque se llena de oxígeno (O2), contiene 10.0 kg de gas a una presión manométrica de 40.0 atm. Determina la masa de oxígeno que se ha extraído del tanque cuando se mide una presión manométrica de 25.0 atm. Supón que la temperatura de tanque permanece constante.
4 Presión en un neumático
Un neumático de un automóvil se infla con aire que inicialmente se encuentra a una temperatura de 10.0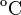
y a presión atmosférica normal. Durante el proceso, el aire se comprime hasta alcanzar el 28.0% de su volumen original, lo que hace que aumente su temperatura a 40.0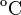
- ¿Cuál es la presión en el neumático?
- Después de hacer circular el coche a gran velocidad, la temperatura en el interior del neumático aumenta hasta 85.0 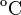y su volumen aumenta en un 2.00%. ¿Cuál es la nueva presión (absoluta) del neumático expresada en pascales?
5 Pistón oscilante
Un cilindro de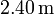 
de altura se llena con 0.100 moles de un gas ideal a una temperatura de 
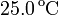y una presión de 
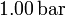. El cilindro se cierra entonces con un pistón de masa 
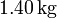que se deja caer hasta alcanzar el equilibrio.
- Determina la altura h0 del pistón suponiendo que la temperatura del gas no varía en la compresión.
- Supón que el pistón se empuja hacia abajo ligeramente más allá de la posición de equilibrio y luego se libera. Suponiendo que la temperatura del gas permanece constante y que el rozamiento del pistón es despreciable, demuestra que el pistón describe un movimiento armónico simple y determina su frecuencia.
