Problemas de dinámica de los sistemas de partículas (GIOI)
De Laplace
1 Centro de masas de cuatro partículas en un cuadrado
Se tienen 4 masas que ocupan los vértices de un cuadrado de lado 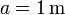 . Calcule la posición del centro de masas del sistema en cada uno de los casos siguientes
. Calcule la posición del centro de masas del sistema en cada uno de los casos siguientes
 .
.
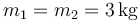 ,
, 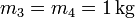 .
.
 ,
, 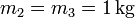 .
.
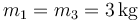 ,
, 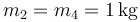 .
.
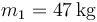 ,
,  .
.

2 Centro de masas de una L
Se tiene un sólido en forma de L con los brazos de igual longitud h, siendo m la masa total del sólido, distribuida uniformemente.
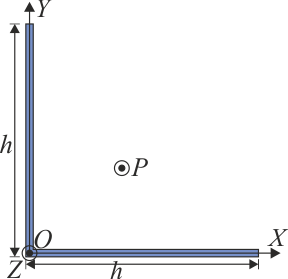
Considerando un sistema de ejes con origen en el vértice y ejes OX y OY paralelos a los brazos de la L, ¿dónde se encuentra en centro de masas del sólido?
3 Propiedades de un sistema de tres partículas
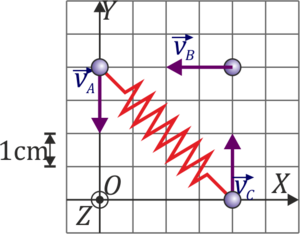
Considere un sistema de tres partículas de masas 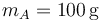 ,
, 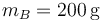 ,
,  que en un instante dado están situadas en las posiciones de la figura y moviéndose con la velocidad indicada, siendo la rapidez de cada una de ellas
que en un instante dado están situadas en las posiciones de la figura y moviéndose con la velocidad indicada, siendo la rapidez de cada una de ellas  . Suponga
que la masa A y la C está unidas por un resorte de longitud natural nula y constante
. Suponga
que la masa A y la C está unidas por un resorte de longitud natural nula y constante 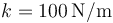 . Para el instante indicado
. Para el instante indicado
- Halle la posición del centro de masas (CM) del sistema.
- Calcule la cantidad de movimiento del sistema.
- Halle el momento cinético respecto al origen y respecto al CM.
- Calcule la energía cinética del sistema respecto a un sistema fijo y respecto al CM.
- Halle la aceleración de cada masa y la del CM.
- Halle la derivada respecto al tiempo del momento cinético (calculado respecto al origen).
- Calcule la derivada respecto al tiempo de la energía cinética del sistema (calculada respecto a un sistema fijo).
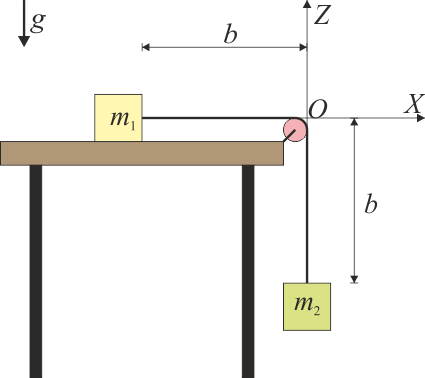
4 Máquina de Atwood y momento cinético
Considere una máquina de Atwood ideal formada por dos masas m1 y m2 que cuelgan de una polea (ideal, sin rozamiento ni masa) de radio b, a través de un hilo también ideal (inextensible y sin masa) de longitud 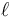 . Inicialmente las dos masas están en reposo a la misma altura.
. Inicialmente las dos masas están en reposo a la misma altura.
- Determine la masa total, la posición, velocidad y aceleración del centro de masas, la cantidad de movimiento, el momento cinético respecto al centro de la polea y la energía cinética del sistema, todo ello como función del tiempo.
- A partir del teorema del momento cinético, calcule la aceleración que adquieren las dos masas.
- Para la cantidad de movimiento, el momento cinético respecto al centro de la polea y la energía cinética determine sus derivadas respecto al tiempo y compruebe que se satisfacen las leyes para su evolución.
5 Cañón casero
Se puede construir un sencillo cañón casero para disparos en vertical de la siguiente manera: se toma un tubo vertical de longitud L (tómese 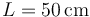 ) cuyo extremo inferior se apoya en el suelo. Por su interior se dejan caer prácticamente seguidas dos bolas, siendo la inferior mucho más pesada que la superior (por ejemplo, una bola de acero y una pelota de ping-pong). Estime la altura máxima a la que subiría la bola ligera tras los rebotes. Justifique las aproximaciones que se efectúen.
) cuyo extremo inferior se apoya en el suelo. Por su interior se dejan caer prácticamente seguidas dos bolas, siendo la inferior mucho más pesada que la superior (por ejemplo, una bola de acero y una pelota de ping-pong). Estime la altura máxima a la que subiría la bola ligera tras los rebotes. Justifique las aproximaciones que se efectúen.
6 Péndulo balístico
Un péndulo balístico es un dispositivo elemental para determinar la velocidad de un proyectil. Consiste en un bloque pesado de madera, de masa M que pende de un hilo de longitud L. Sobre este bloque, inicialmente en reposo, impacta una bala de masa m que se mueve, justo antes del impacto, con velocidad v0, quedándose empotrada en el bloque. Determine el ángulo máximo de desviación del péndulo respecto a la vertical. Si lo que se mide es el ángulo, obtenga una expresión para la velocidad de impacto.
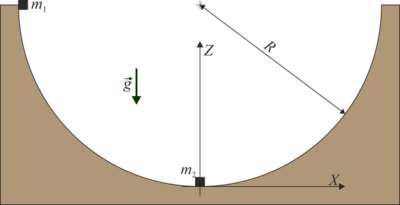
7 Colisión en el interior de un cuenco
En el interior de un cuenco hemisférico de radio 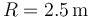 cuyo borde es horizontal, se encuentran dos partículas que pueden deslizar sin rozamiento por su superficie. Una de ellas, de masa
cuyo borde es horizontal, se encuentran dos partículas que pueden deslizar sin rozamiento por su superficie. Una de ellas, de masa 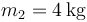 , se encuentra en reposo en el fondo del cuenco. La otra, de masa
, se encuentra en reposo en el fondo del cuenco. La otra, de masa 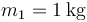 se coloca en el borde del cuenco y desde allí se suelta.
se coloca en el borde del cuenco y desde allí se suelta.
- Calcule, con justificación, la velocidad que lleva la masa 1 justo antes de impactar con la masa 2. Halle la reacción del cuenco sobre la masa 1 para el mismo instante.
- Si el choque es perfectamente elástico, calcule las velocidades de las dos masas justo tras la colisión.
- Para este caso elástico, halle la altura máxima desde el fondo del cuenco que alcanza cada una de las masas tras el choque.
- Repita los dos apartados anteriores para el caso de que la colisión sea completamente inelástica. ¿Cuánta energía se pierde en la colisión en ese caso?
Tómese g = 9.8m/s²
8 Masa arrastrada sobre una mesa
Se tiene un sistema de 2 masas de 4 kg cada una, atadas por una cuerda ideal, inextensible y sin masa, que pasa por una polea también ideal. La masa 1 está sobre una superficie horizontal sin rozamiento, mientras que la 2 cuelga verticalmente.
Empleando el sistema de ejes de la figura y para el instante reflejado en ella:
- ¿Cuál es la aceleración de cada una de las masas?
- ¿Dónde se halla el centro de masas?
- ¿Cuál es la aceleración del CM?
- Si en el instante representado la masa 1 tiene una rapidez v0, ¿cuánto vale la velocidad del CM?
- Para el caso de apartado anterior, ¿cuánto valen la cantidad de movimiento, la energía cinética y el momento cinético respecto al origen y respecto al CM?
9 Colisión con rozamiento
Sobre una superficie horizontal se encuentran dos masas. La masa 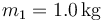 se encuentra inicialmente en
se encuentra inicialmente en 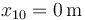 y la masa
y la masa 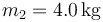 en
en 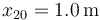 . La masa 2 está unida a un resorte de constante
. La masa 2 está unida a un resorte de constante 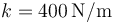 y longitud en reposo
y longitud en reposo 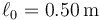 , estando inicialmente en la posición de equilibrio. El tramo de 1 m entre la masa 1 y la 2 es una superficie rugosa, en la que la constante de rozamiento vale μ = 0.45. El resto de la superficie está pulido.
, estando inicialmente en la posición de equilibrio. El tramo de 1 m entre la masa 1 y la 2 es una superficie rugosa, en la que la constante de rozamiento vale μ = 0.45. El resto de la superficie está pulido.
Estando las dos masas en reposo se le aplica una percusión a la masa 1 de forma que esta adquiere una velocidad inicial 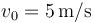
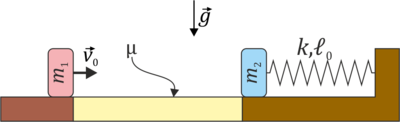
- Determine la velocidad de m1 justo antes de impactar con la masa 2.
- Calcule las velocidades de ambas masas justo tras el impacto. Suponga que la colisión es perfectamente elástica.
- Halle la posición x1f en la que se detiene la masa 1, si llega a hacerlo. Si no se detiene, halle la velocidad con la que llega a su posición inicial.
- Halle la posición x2f en la que se detiene m_2 por primera vez.
Tómese 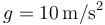 .
.
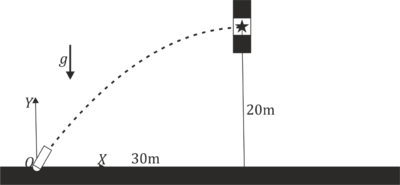
10 Colisión en tiro parabólico
En un videojuego que reproduce correctamente las leyes de la física, es preciso golpear una masa de 0.80 kg encajada entre un bloque fijo por abajo y uno idéntico por arriba, de manera que la única forma de sacarlo es mediante un golpe horizontal. Para ello se dispone de un cañón que lanza un proyectil de 0.20kg desde un punto situado a 30m en la horizontal y 20m en la vertical.
- Calcule la velocidad inicial que debe tener el proyectil para impactar el blanco de forma horizontal. ¿Cuánto vale la rapidez inicial? ¿Qué ángulo debe formar la velocidad inicial con el suelo?
- Suponiendo que la colisión es elástica, halle
- Las velocidades del proyectil y el blanco justo tras la colisión
- Las posiciones donde proyectil y blanco impactan con el suelo.
- La proporción de la energía mecánica inicial que tiene el proyectil y la que tiene el blanco en el momento del impacto con el suelo. Tómese este suelo como origen de la energía potencial.
- Suponiendo ahora que la colisión es completamente inelástica, de forma que el proyectil queda empotrado en el blanco, halle:
- La velocidad del conjunto justo tras la colisión
- La posición donde impacta con el suelo.
- La proporción de la energía mecánica inicial que se ha perdido desde el lanzamiento al impacto final.
Tómese g = 10m/s². Desprecie el rozamiento con el aire. Suponga que el proyectil y el blanco son partículas puntuales.