Masa arrastrada sobre una mesa

De Laplace

Contenido

1 Enunciado
2 Aceleraciones
3 Posición del CM
4 Aceleración del CM
5 Velocidad del CM
6 Propiedades del sistema

1 Enunciado

Se tiene un sistema de 2 masas de 4 kg cada una, atadas por una cuerda ideal, inextensible y sin masa, que pasa por una polea también ideal. La masa 1 está sobre una superficie horizontal sin rozamiento, mientras que la 2 cuelga verticalmente.

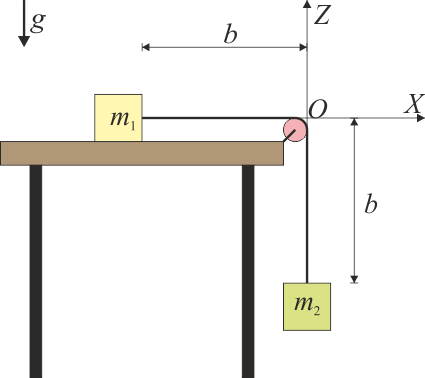
Empleando el sistema de ejes de la figura y para el instante reflejado en ella:

¿Cuál es la aceleración de cada una de las masas?
¿Dónde se halla el centro de masas?
¿Cuál es la aceleración del CM?
Si en el isntante representado la masa 1 tiene una rapidez $v 0$ , ¿cuánto vale la velocidad del CM?
Para el caso de apartado anterior, ¿cuánto valen la cantidad de movimiento, la energía cinética y el momento cinético respecto al origen y respecto al CM?

2 Aceleraciones

Este sistema es un caso particular de otro estudiado en un problema de dinámica. Para calcular las aceleraciones respectivas realizamos los diagramas de cuerpo libre, considerando cada masa por separado, incluyendo todas las fuerzas que actúan sobre ellas.

Sobre la masa 1 actúan tres fuerzas: su peso, la reacción normal de la mesa y la tensión de la cuerda que tira de ella. Si hubiera rozamiento también deberíamos incluirlo, pero no es el caso. Por tanto tenemos

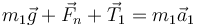
$m_1\vec{g}+\vec{F}_n + \vec{T}_1 = m_1\vec{a}_1$

Para la segunda masa las únicas fuerzas que actúan son su peso y la tensión que tiera de ella hacia arriba

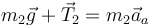
$m_2\vec{g}+\vec{T}_2=m_2\vec{a}_a$

Separando en componentes cada una de estas ecuaciones tenemos, para la primera masa

$T_1=m_1a_1\qquad\qquad -m_1g+F_n = 0$

ya que su aceleración es puramente horizontal. Para la segunda masa obtenemos una sola ecuación escalar

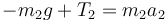
$-m_2g+T_2=m_2a_2\,$

Por tratarse de un hilo ideal sin masa, el módulo de la tensión en el extremo de la masa 1 es igual al del otro extremo

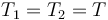
$T_1=T_2 = T\,$

y por ser inextensible la rapidez y la aceleración horizontal de la masa 1 debe coincidir con la de la masa 2,

$v_1 = -v_2\qquad\qquad a_1 = -a_2$

El signo negativo proviene de que, de acuerdo con el sistema de ejes elegido hemos considerado

$\vec{a}_1=a_1\vec{\imath}\qquad\qquad\vec{a}_2=a_2\vec{k}$

es decir, ambas dirigidas hacia la polea, por lo que una de ellas debe ser negativa.

Con estas simplificaciones queda el sistema

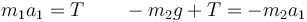
$m_1a_1 = T\qquad -m_2g+T=-m_2a_1$

Sumando las dos ecuaciones hallamos las aceleraciones

$a_1 = \frac{m_2}{m_1+m_2}g\qquad\qquad a_2 = -\frac{m_2}{m_1+m_2}g$

y, en forma vectorial,

$\vec{a}_1 = \frac{m_2}{m_1+m_2}g\vec{\imath}\qquad\qquad \vec{a}_2 = -\frac{m_2}{m_1+m_2}g\vec{k}$

En el caso particular $m 1 = m 2 = m$

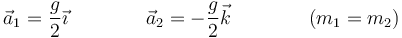
$\vec{a}_1 = \frac{g}{2}\vec{\imath}\qquad\qquad\vec{a}_2=-\frac{g}{2}\vec{k}\qquad\qquad(m_1=m_2)$

Asimismo, podemos calcular las diferentes fuerzas de reacción vincular. La reacción de la mesa es opuesta al peso de la masa situada sobre ella

$-m_1g+F_n = 0 \qquad\Rightarrow\quad\vec{F}_n = m_1g\vec{k}$

mientras que las tensiones en los extremos de la cuerda valen, en el primer caso

$\vec{T}_1 = m_1a_1\vec{\imath}=\frac{m_1m_2}{m_1+m_2}g\vec{\imath}$

y en el segundo

$\vec{T}_2 = m_2\vec{a}_2-m_2\vec{g} = \frac{m_1m_2}{m_1+m_2}g\vec{k}$

Estas dos fuerzas son iguales en módulo, pero no en dirección y sentido, es decir, no se trata de fuerzas opuestas.

3 Posición del CM

El centro de masas es la media ponderada de las posiciones respectivas

$\vec{r}_C=\frac{m_1\vec{r}_1+m_2\vec{r}_2}{m_1+m_2}$

para la posición de la figura

$\vec{r}_1 = -b\vec{\imath}\qquad\qquad \vec{r}_2=-b\vec{k}$

resulta la posición del CM

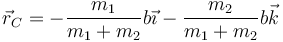
$\vec{r}_C = -\frac{m_1}{m_1+m_2}b\vec{\imath}-\frac{m_2}{m_1+m_2}b\vec{k}$

Este punto se halla sobre la recta que une las dos partículas (o, para ser precisos, sus respectivos centros de masas). Si además las dos masas son iguales, el centro de masas se halla en el punto medio entre ellas

$\vec{r}_C = -\frac{b}{2}\vec{\imath}-\frac{b}{2}\vec{k}\qquad\qquad(m_1=m_2)$

4 Aceleración del CM

De manera análoga hallamos la aceleración del centro de masas

$\vec{a}_C =\frac{m_1\vec{a}_1+m_2\vec{a}_2}{m_1+m_2}$

que en este caso nos da

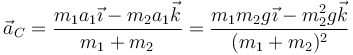
$\vec{a}_C=\frac{m_1a_1\vec{\imath}-m_2a_1\vec{k}}{m_1+m_2}=\frac{m_1m_2g\vec{\imath}-m_2^2g\vec{k}}{(m_1+m_2)^2}$

si además las masas son iguales

$\vec{a}_C = \frac{g}{4}\vec{\imath}-\frac{g}{4}\vec{k}\qquad\qquad (m_1=m_2)$

De acuerdo con el teorema para la cantidad de movimiento en un sistema de partículas, esta aceleración satisface

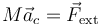
$M\vec{a}_c = \vec{F}_\mathrm{ext}$

siendo $\vec{F}_\mathrm{ext}$ la resultante 8suma vectorial) de todas las fuerzas externas aplicadas. Por tanto, tenemos

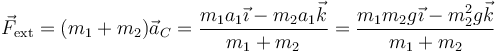
$\vec{F}_\mathrm{ext}=(m_1+m_2)\vec{a}_C = \frac{m_1a_1\vec{\imath}-m_2a_1\vec{k}}{m_1+m_2}=\frac{m_1m_2g\vec{\imath}-m_2^2g\vec{k}}{m_1+m_2}$

Ahora bien, cuando hablamos de “fuerzas externas”, ¿a cuáles nos estamos refiriendo? Tenemos el peso de la masa 1, que es compensado por la reacción de la mesa (también una fuerza externa), el peso de la masa 2, ¿y cuál más? La respuesta es que también debemos contar las tensiones de la cuerda

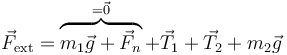
$\vec{F}_\mathrm{ext}=\overbrace{m_1\vec{g}+\vec{F}_n}^{=\vec{0}}+\vec{T}_1+\vec{T}_2+m_2\vec{g}$

puesto que las dos tensiones no son iguales y opuestas (aunque tienen el mismo módulo), no se anulan mutuamente y también deben incluirse en las fuerzas externas.

Ahora bien, podemos considerar que la cuerda es parte del sistema. Puesto que no tiene masa, no afecta a la posición o a la aceleración del CM, pero ahora la tensión pasa a ser una fuerza interna. En ese caso, ¿qué fuerza externa produce la aceleración del CM? En concreto, ¿quién tira de la masa 1? Obviamente la cuerda, pero, ¿quién tira de la cuerda? La tentación es decir el peso de la masa 2, pero eso no puede ser correcto. El peso es una fuerza vertical, que nunca va a producir una aceleración horizontal. Debe haber, en algún punto del sistema masas+cuerda, una fuerza externa que tenga componente horizontal. La respuesta es que esta fuerza la produce la polea por la que pasa la cuerda.

Consideremos las fuerzas que actúan sobre la polea: la cuerda por la parte de arriba ejerce una fuerza 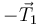$-\vec{T}_1$ y por la parte de abajo una fuerza 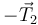$-\vec{T}_2$ . El resultado es que la cuerda ejerce sobre la polea una fuerza neta

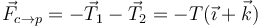
$\vec{F}_{c\to p}=-\vec{T}_1-\vec{T}_2=-T(\vec{\imath}+\vec{k})$

Esta fuerza es diagonal hacia adentro de la mesa (y podría llegar a romper la polea, si ésta es débil). Por la tecera ley de Newton, la polea debe ejercer una fuerza igual y de sentido opuesto a la anterior

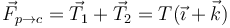
$\vec{F}_{p\to c}=\vec{T}_1+\vec{T}_2=T(\vec{\imath}+\vec{k})$

Es esta fuerza la responsable de que la aceleración del CM tenga una componente horizontal. Por tanto, en el sistema masas+cuerda, las fuerzas externas son:

El peso de cada masa
La reacción del plano sobre $m 1$
La fuerza que la polea ejerce sobre la cuerda.

La suma de estas tres iguala al producto de la masa total por la aceleración del centro de masas.

5 Velocidad del CM

De la misma manera se calcula la velocidad del centro de masas

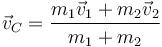
$\vec{v}_C=\frac{m_1\vec{v}_1+m_2\vec{v}_2}{m_1+m_2}$

siendo

$\vec{v}_1 = v_0\vec{\imath}\qquad \qquad \vec{v}_2=-v_0\vec{k}$

obtenemos

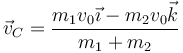
$\vec{v}_C=\frac{m_1v_0\vec{\imath}-m_2v_0\vec{k}}{m_1+m_2}$

que para el caso particular de dos masas iguales da

$\vec{v}_C=\frac{v_0}{2}\vec{\imath}-\frac{v_0}{2}\vec{k}\qquad\qquad (m_1=m_2)$

6 Propiedades del sistema

6.1 Cantidad de movimiento

La cantidad de movimiento del sistema ya la hemos calculado para hallar la velocidad del centro de masas

$\vec{p}=m_1\vec{v}_1+m_2\vec{v}_2=m_1v_0\vec{\imath}-m_2v_0\vec{k}$

Si las masas son iguales

$\vec{p}=mv_0(\vec{\imath}-\vec{k})\qquad\qquad (m_1=m_2=m)$

6.2 Energía cinética

La energía cinética respecto al sistema fijo se calcula de forma inmediata

$K = \frac{1}{2}m_1|\vec{v}_1|^2+\frac{1}{2}m_2|\vec{v}_2|^2 = \frac{1}{2}(m_1+m_2)v_0^2$

Esta energía se puede descomponer en suma de dos términos, uno el que tendría el sistema si toda la masa estuviera concentrada en el CM

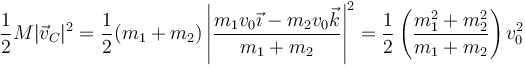
$\frac{1}{2}M|\vec{v}_C|^2 = \frac{1}{2}(m_1+m_2)\left|\frac{m_1v_0\vec{\imath}-m_2v_0\vec{k}}{m_1+m_2}\right|^2 = \frac{1}{2}\left(\frac{m_1^2+m_2^2}{m_1+m_2}\right)v_0^2$

y otro correspondiente al movimiento alrededor del CM

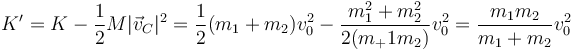
$K' = K - \frac{1}{2}M|\vec{v}_C|^2 = \frac{1}{2}(m_1+m_2)v_0^2-\frac{m_1^2+m_2^2}{2(m_+1m_2)}v_0^2 =\frac{m_1m_2}{m_1+m_2}v_0^2$

Podemos hallar esta energía cinética relativa al CM calculando en primer lugar las velocidades relativas. Para la masa que está sobre la mesa

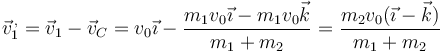
$\vec{v}_1^{\,,}=\vec{v}_1-\vec{v}_C = v_0\vec{\imath}-\frac{m_1v_0\vec{\imath}-m_1v_0\vec{k}}{m_1+m_2}=\frac{m_2v_0(\vec{\imath}-\vec{k})}{m_1+m_2}$

y para la que cuelga

$\vec{v}_2^{\,,}=\vec{v}_2-\vec{v}_C = -v_0\vec{k}-\frac{m_1v_0\vec{\imath}-m_1v_0\vec{k}}{m_1+m_2}=\frac{m_1v_0(-\vec{\imath}+\vec{k})}{m_1+m_2}$

cumpliéndose

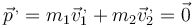
$\vec{p}^{\,,}=m_1\vec{v}_1^{\,,}+m_2\vec{v}_2^{\,,}=\vec{0}$

Con estas velocidades relativas hallamos la energía cinética en el sistema centro de masas

$K' =\frac{1}{2}m_1|\vec{v}_1^{\,,}|^2+\frac{1}{2}m_2|\vec{v}_2^{\,,}|^2=\frac{1}{2}\frac{2m_1m_2^2+2m_2m_1^2}{(m_1+m_2)^2}v_0^2=\frac{m_1m_2}{(m_1++m_2}v_0^2$

En el caso particular de dos masas iguales la energía cinética total es

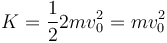
$K = \frac{1}{2}2mv_0^2 = mv_0^2$

La que tendría el sistema si se moviera con el CM

$\frac{1}{2}M|\vec{v}_C|^2 = \frac{1}{2}(2m)\left(\frac{v_0^2}{4}+\frac{v_0^2}{4}\right)=\frac{1}{2}mv_0^2$

que es la mitad de la anterior. La energía del movimiento alrededor del CM será la otra mitad

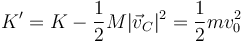
$K' = K -\frac{1}{2}M|\vec{v}_C|^2=\frac{1}{2}mv_0^2$

6.3 Momento cinético

El momento cinético respecto al punto O es nulo, ya que la velocidad de cada masa es paralela a su vector de posición en este sistema

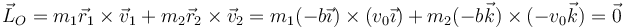
$\vec{L}_O=m_1\vec{r}_1\times\vec{v}_1+m_2\vec{r}_2\times\vec{v}_2=m_1(-b\vec{\imath})\times(v_0\vec{\imath})+m_2(-b\vec{k})\times(-v_0\vec{k})=\vec{0}$

El momento cinético también se puede escribir como una suma del que tendría si toda la masa estuviera en el CM

$M\vec{r}_C\times\vec{v}_C=(m_1+m_2)\left(-\frac{m_1b}{m_1+m_2}\vec{\imath}-\frac{m_2b}{m_1+m_2}\vec{k}\right)\times\left(\frac{m_1v_0}{m_1+m_2}\vec{\imath}-\frac{m_2v_0}{m_1+m_2}\vec{k}\right)=-\frac{2m_1m_2bv_0}{m_1+m_2}\vec{\jmath}$

y del que tiene respecto al centro de masas

$\vec{L}^{\,,}=m_1\vec{r}_1^{\,,}\times\vec{v}_1^{\,,}+m_2\vec{r}_2^{\,,}\times\vec{v}_2^{\,,} = \frac{2m_1m_2bv_0}{m_1+m_2}\vec{\jmath}$

En el caso particular de dos masas iguales

$\vec{L}=\vec{0}\qquad\qquad M\vec{r}_C\times\vec{v}_C = -mbv_0\vec{\jmath}\qquad\qquad \vec{L}'=+mbv_0\vec{\jmath}$

Masa arrastrada sobre una mesa

De Laplace

Contenido

1 Enunciado

2 Aceleraciones

3 Posición del CM

4 Aceleración del CM

5 Velocidad del CM

6 Propiedades del sistema

6.1 Cantidad de movimiento

6.2 Energía cinética

6.3 Momento cinético

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES