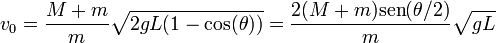Péndulo balístico
De Laplace
1 Enunciado
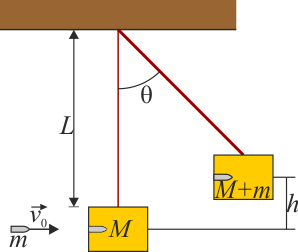
Un péndulo balístico es un dispositivo elemental para determinar la velocidad de un proyectil. Consiste en un bloque pesado de madera, de masa M que pende de un hilo de longitud L. Sobre este bloque, inicialmente en reposo, impacta una bala de masa m que se mueve, justo antes del impacto, con velocidad v0, quedándose empotrada en el bloque. Determine el ángulo máximo de desviación del péndulo respecto a la vertical. Si lo que se mide es el ángulo, obtenga una expresión para la velocidad de impacto.
2 Solución
En un péndulo balístico tenemos una colisión completamente inelástica, ya que la bala se queda empotrada en el péndulo. Esto quiere decir que en la colisión no se conserva la energía. Esto es importante, ya que existe la tentación de suponer que la energía potencial final iguala a la cinética inicial, sin tener en cuenta la disipación de la energía en la colisión.
La solución se compone de dos partes. Primero estudiamos la colisión inelástica ntre la bala y el péndulo para obtener la velocidad del conjunto justo tras la colisión. En segundo lugar aplicamos la ley de conservación de la energía mecánica para determinar la altura a la que sube el péndulo (o el ángulo de desviación que es equivalente).
En el choque del proyectil con el péndulo se conserva la cantidad de movimiento. Inicialmente tenemos una bala de masa m y rapidezv0 que choca con el péndulo en reposo. Tras el choque, lo que hay es un conjunto de masa M + m tal que
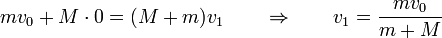
El péndulo se eleva como consecuencia de esta velocidad inicial. Puesto que la tensión es una fuerza puramente normal, la única energía potencial es la debida a la gravedad. La altura máxima se alcanza cuando la energía cinética se reduce a cero y toda la energía mecánica es potencial. Igualando la energía mecánica justo tras la colisión con la final
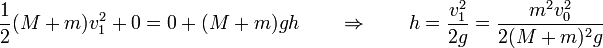
En términos del ángulo girado queda
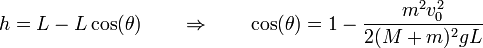
Si lo que queremos es conocer la rapidez de la bala en función del ángulo girado, invertimos la relación