Máquina de Atwood y momento cinético

De Laplace

1 Enunciado

Considere una máquina de Atwood ideal formada por dos masas m₁ y m₂ que cuelgan de una polea (ideal, sin rozamiento ni masa) de radio b, a través de un hilo también ideal (inextensible y sin masa) de longitud 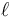. Inicialmente las dos masas están en reposo a la misma altura.

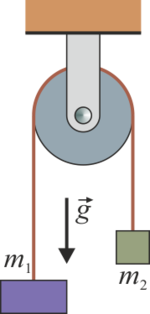
1. Determine la masa total, la posición, velocidad y aceleración del centro de masas, la cantidad de movimiento, el momento cinético respecto al centro de la polea y la energía cinética del sistema, todo ello como función del tiempo.
2. A partir del teorema del momento cinético, calcule la aceleración que adquieren las dos masas.
3. Para la cantidad de movimiento, el momento cinético respecto al centro de la polea y la energía cinética determine sus derivadas respecto al tiempo y compruebe que se satisfacen las leyes para su evolución.

2 Propiedades del sistema

2.1 Masa total

2.2 Posición del CM

2.3 Velocidad del CM

2.4 Aceleración del CM

2.5 Cantidad de movimiento

2.6 Momento cinético

2.7 Energía cinética

3 Aplicación del TMC

4 Evolución de las diferentes magnitudes