Primera convocatoria 2017/18 (F2GIA)

De Laplace

Contenido 1 Fuerza eléctrica en sistema de cuatro cargas puntuales 2 Campo eléctrico de distribución volumétrica de carga con simetría radial 3 Potencial en sistema de conductores planos con medio inhomogéneo 4 Condensador plano paralelo 5 Determinación del material de un cable conductor 6 Campo magnético en el plano de simetría de dos corrientes rectilíneas 7 Bobina cortocircuitada sometida a campo externo 8 Proceso cíclico reversible de un gas ideal

1 Fuerza eléctrica en sistema de cuatro cargas puntuales

Dos cargas eléctricas puntuales idénticas de valor Q, ocupan sendos puntos A y C que, en un sistema de referencia OXYZ, tienen coordenadas cartesianas A(a,0,0) y C( − a,0,0). Otras dos cargas idénticas entre sí y de valor q, ocupan los puntos B y D del eje OY, cuyas coordenadas cartesianas son B(0,b,0) y D(0, − b,0). La geometría

del sistema es tal que la distancia que separa dos carta contiguas es

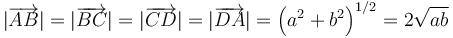
No existen más cargas eléctricas, a parte de las cuatro que constituyen el sistema descrito.

1. ¿Qué relación deben verificar la cantidades de Q y q de las respectivas cargas puntuales descritas en el sistema para que la fuerza eléctrica resultante que actúa sobre la carga que ocupa el punto A sea nula, ?
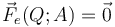2. En las condiciones del apartado anterior, ¿cómo es la fuerza eléctrica resultante que actúa sobre cada una de las otras tres cargas?

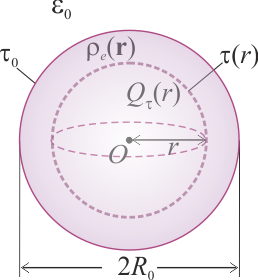
2 Campo eléctrico de distribución volumétrica de carga con simetría radial

En una esfera τ₀ de radio R₀ y centro en O, existe una distribución no uniforme de carga eléctrica negativa descrita por una densidad volumétrica radial ρ_e(r), respecto del punto O, de manera que r es la distancia desde dicho centro al punto P donde se mide la densidad de carga. Dicha distribución es tal que si consideramos una región esférica τ con centro en O y radio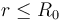 , la cantidad parcial de carga contenida en τ es 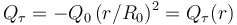. No hay más cargas en el sistema.

1. ¿Cómo es la componente radial del campo eléctrico E(r) creado por la distribución descrita, tanto dentro como fuera de la esfera τ₀?
2. ¿Cómo es el potencial electrostático creado por la distribución en el exterior de τ₀? ¿Cuánto vale el potencial en el centro O?

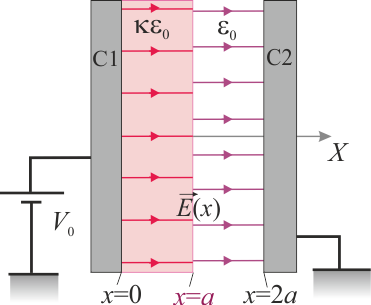
3 Potencial en sistema de conductores planos con medio inhomogéneo

Dos cuerpos conductores,C₁ y C₂, presentan sendas superficies planas, perpendiculares al eje OX, que coinciden con los planos geométricos Π₁:x = 0 y con Π₂:x = 2a. La distancia de separación, 2a, es significativamente menor que las dimensiones de los planos conductores. La región correspondiente a 0 < x < a está ocupada por un dieléctrico lineal de constante dieléctrica κ, mientras que la comprendida en el intervalo a < x < 2a está rellena de aire. El conductor C₁ está conectado a un generador cuya f.e.m. tiene un valor constante V₀, y el C₂ a tierra. Esta diferencia de potencial entre los conductores determina la presencia de un campo eléctrico en la región dieléctrica que los separa, y cuya expresión es:

1. ¿Cómo son las superficies equipotenciales entre los dos conductores? Indique de qué forma varía el valor del potencial de dichas superficies.
2. ¿Qué relación existe entre los valores V₀ y E₀? Obtenga la función V(x) que describe cómo es el valor del potencial en la región 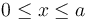(dieléctrico lineal), y en 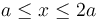(aire).

4 Condensador plano paralelo

Se tienen dos discos conductores idénticos, de radio 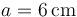, con los que se quiere construir un condensador plano-paralelo de capacidad eléctrica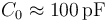

1. Si los conductores están separados por aire, cuyo campo de ruptura es 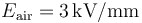, ¿qué distancia debe existir entre los discos conductores? ¿Cuál es el máximo valor de diferencia de potencial que puede aplicarse entre los discos?
2. Si se separan por una lámina de papel de espesor 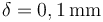, cuya constante de dieléctrica es 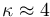, y cuyo campo de ruptura es 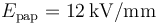, ¿cuál será la capacidad eléctrica y la diferencia de potencial que puede aplicarse?

5 Determinación del material de un cable conductor

Un conductor filiforme, de un material desconocido, tiene una sección uniforme de área 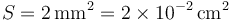. Para determinar el tipo de material, se hace que por el hilo conductor circule una corriente estacionaria de intensidad 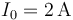y, con la ayuda de un voltímetro, se determinan dos puntos A y B en el hilo tales que la diferencia de potencial entre ellos sea 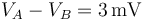. Se determina que la longitud del hilo comprendida entre dichos puntos es .

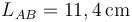1. Calcule la conductividad del hilo e indique de qué material está fabricado.
2. Haga una estimación de los valores de la intensidad del campo eléctrico (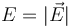), y de la densidad volumétrica (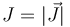), en el interior del cable.

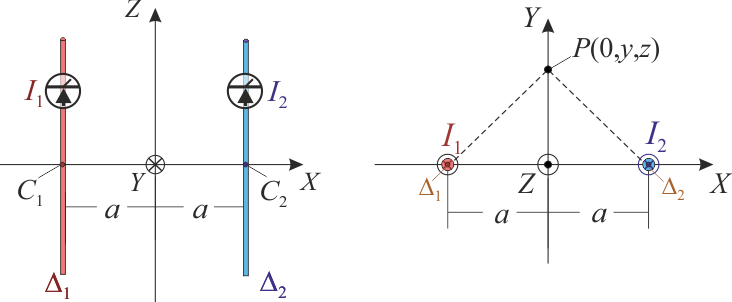
6 Campo magnético en el plano de simetría de dos corrientes rectilíneas

Dos conductores filiformes rectilíneos de longitud indefinida, Δ₁ y Δ₂, están dispuestos en el plano OXZ, en paralelo al eje OZ y a igual distancia a de éste, de manera que pasan por los puntos C₁( − a,0,0) y C₂(a,0,0), respectivamente. Los conductores soportan sendas corrientes eléctricas cuyas intensidades, I₁ e I₂, son medidas por amperímetros que indican valores positivos si las corrientes recorren los hilos en el sentido de “z” creciente, y negativos si lo hacen en el sentido de “z” decreciente. Describa cómo es la dirección, el sentido y el módulo del campo magnético total en los puntos de coordenadas P(0,y,z) situados en el plano 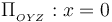(plano cartesiano OYZ), en las siguientes situaciones:

1. Las corrientes en los conductores son opuestas: I₁ = − I₂ = I₀ > 0.
2. Las corrientes en los conductores son iguales y descendentes: I₁ = I₂ = − I₀ < 0.

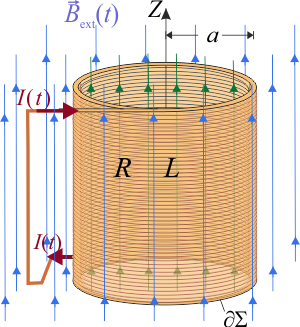
7 Bobina cortocircuitada sometida a campo externo

Una bobina de resistencia eléctrica 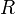y autoinducción 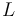está formada por N espiras idénticas de radio 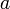, todas perpendiculares al eje OZ que pasa por sus centros. La espira está cortocircuitada y sometida a un campo magnético externo uniforme y variable en el tiempo 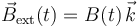. El resultado es que la bobina es recorrida por una intensidad de corriente 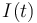medida en el sentido antihorario.

1. Obtenga la expresión del flujo magnético total a través de las N espiras que forman la bobina (no olvidar que su autoinducción tiene un valor apreciable).
2. Aplique las leyes de la inducción electromagnética para determinar cómo deber ser la ley horaria 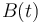que verifica el campo magnético externo para que la bobina sea recorrida por una corriente eléctrica de intensidad constante, I₀.
3. En las condiciones del apartado anterior, ¿qué energía magnética se almacena en la bobina? ¿Qué cantidad de energía por unidad de tiempo se disipa en la bobina por efecto Joule?

8 Proceso cíclico reversible de un gas ideal

Un sistema termodinámico consistente en n moles de un gas ideal monoatómico realiza un proceso cíclico. Inicialmente se encuentra en un estado “A” caracterizado por la terna de valores de presión, volumen y temperatura {P₀,V₀,T₀}. La fase “1” del ciclo consiste en un proceso isócoro (a volumen constante) hasta el estado “B”, en el cuál su temperatura tiene un valor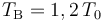 . En la fase “2” se expande isotérmicamente (a temperatura constante), hasta recuperar la presión inicial P₀ en el estado “C”. A continuación realiza otro proceso isócoro “3” hasta el estado “D” para, finalmente, realizar un nuevo proceso isotermo “4” que termina en el estado “A”, completando el ciclo. Se asume que todas las fases del ciclo son procesos reversibles.

1. Obtenga los valores de presión, volumen y temperatura en los estados “B”, “C” y “D”, en función de los correspondientes al estado “A”.
2. En cada fase del proceso cíclico, calcule las cantidades de energía transferida en forma de calor y de trabajo. Determine también la variación de energía interna en cada fase.
3. Calcule el trabajo neto realizado por el sistema en el ciclo (W_out − W_in), y las cantidades de calor absorbido (Q_in), y cedido (Q_out).
4. Calcule el rendimiento de esta máquina térmica, definido como el cociente entre el trabajo neto realizado y el calor absorbido en un ciclo. Compárelo con el rendimiento de una máquina térmica de Carnot que trabajase entre los mismos focos térmicos que la analizada.