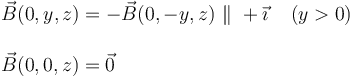Campo magnético en el plano de simetría de dos corrientes filiformes rectilíneas (GIA)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Caso de corrientes estacionarias antiparalelas
- 2.2 Caso de corrientes estacionarias paralelas

1 Enunciado

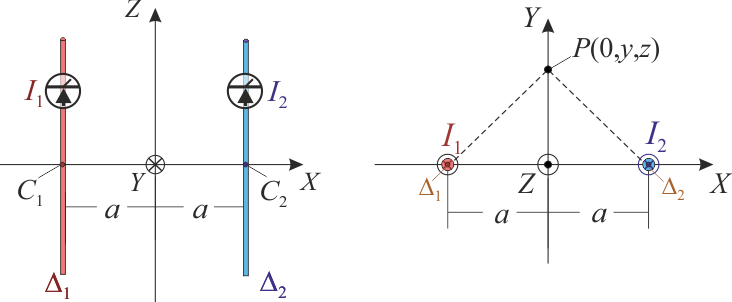
Dos conductores filiformes rectilíneos de longitud indefinida, $Δ 1$ y $Δ 2$ , están dispuestos en el plano $O X Z$ , en paralelo al eje $O Z$ y a igual distancia $a$ de éste, de manera que pasan por los puntos $C 1 ( - a,0,0)$ y $C 2 (a,0,0)$ , respectivamente. Los conductores soportan sendas corrientes eléctricas cuyas intensidades, $I 1$ e $I 2$ , son medidas por amperímetros que indican valores positivos si las corrientes recorren los hilos en el sentido de “ $z$ ” creciente, y negativos si lo hacen en el sentido de “ $z$ ” decreciente. Describa cómo es la dirección, el sentido y el módulo del campo magnético total en los puntos de coordenadas $P (0, y, z)$ situados en el plano 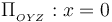$\Pi_{{}_{OYZ}}:x=0$ (plano cartesiano $O Y Z$ ), en las siguientes situaciones:

Las corrientes en los conductores son opuestas: $I 1 = - I 2 = I 0 > 0$ .
Las corrientes en los conductores son iguales y descendentes: $I 1 = I 2 = - I 0 < 0$ .

2 Solución

Campo magnético de corrientes en conductor filiforme rectilíneo

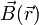La ley de Biot y Savart proporciona la expresión del campo magnético $\vec{B}(\vec{r})$ creado por una corriente eléctrica estacionaria de intensidad

I

, que recorre un conductor filiforme, cualquiera que sea la geometría de éste. El caso particular de un conductor filiforme rectilíneo de longitud indefinida $\displaystyle\Delta$ ha sido analizado con detalle en un ejercicio anterior. Como se vio, dicho campo presenta simetría cilíndrica respecto del conductor rectilíneo. Adoptando un sistema de referencia cuyo eje

O Z

coincida con el conductor $\displaystyle\Delta$ , y utilizando las coordenadas cilíndricas para determinar la posición de un punto $P(\rho,\varphi,z)$ , se tendrá:

el módulo del campo en un punto $P$ sólo depende de su distancia $ρ$ al conductor, siendo inversamente proporcional a dicha distancia (y directamente proporcional a la intensidad de la corriente):

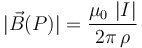
$|\vec{B}(P)|=\frac{\mu_0\ |I|}{2\pi\!\ \rho}$

su dirección en el punto $P$ tiene la dirección tangente a la circunferencia contenida en un plano perpendicular al cable, con centro en éste y que pasa por $P$

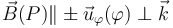
$\vec{B}(P)\| \pm\vec{u}_\varphi (\varphi)\perp \vec{k}$

el sentido del campo depende del sentido de la corriente eléctrica: si ésta recorre el conductor en el sentido creciente de la coordenada “ $z$ ” ( $I > 0$ ), las líneas del campo $\vec{B}(\vec{r})$ “giran” en sentido antihorario; si la corriente circula en el sentido decreciente de “ $z$ ” ( $I < 0$ ), el campo magnético “gira” en sentido horario.

En definitiva, la expresión vectorial del campo mangético en coordenadas cilíndricas es:

$I\,\;\mathrm{en}\,\;\Delta\equiv OZ\;\Longrightarrow\;\vec{B}(P)=\vec{B}(\rho,\varphi,z)=\frac{\mu_0\!\ I}{2\pi\!\ \rho}\ \vec{u}_\varphi(\varphi)$

Sistema de corrientes en dos conductores rectilíneos

En el ejercicio propuesto existen dos conductores filiformes $\displaystyle \Delta_1$ y $\displaystyle \Delta_2$ recorridos por sendas corrientes corrientes de intensidades $I 1$ e $I 2$ . Los campos magnéticos verifican el principio de superposición, por lo que el campo magnético resultante en cada punto será la suma vectorial de los por cada una de las corrientes rectilíneas por separado:

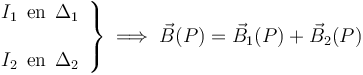
$\left.\begin{array}{l}I_1\,\;\mathrm{en}\,\;\Delta_1\\ \\ I_2\,\;\mathrm{en}\,\;\Delta_2\end{array}\right\}\;\Longrightarrow\;\vec{B}(P)=\vec{B}_1(P)+\vec{B}_2(P)$

Para la obtención de las expresiones analíticas del campo resultante es necesario proceder primero a redefinir el sistema de referencia, ya que el eje $O Z$ no puede estar localizado simultáneamente en los dos conductores rectilíneos. Y puesto que ambos son paralelos, separados por una distancia $2 a$ , una adecuada elección del sistema de referencia $O X Y Z$ podría ser la indicada en el enunciado: el eje $O Z$ paralelo a los hilos condutores, de manera que éstos estén contenidos en el plano $\displaystyle \Pi_{{}_{OXZ}}:y=0$ (plano $O X Z$ ). Además, el $\displaystyle \Pi_{{}_{OYZ}}:x=0$ (plano $O Y Z$ ) va a ser el plano de simetría del sistema, de manera que cada punto $P (0, y, z)$ de dicho plano equidista de ambos conductores.

Los vectores que describen los campos magnéticos creados por cada una de las corrientes en un punto arbitrario $P (x, y, z)$ se pueden expresar analíticamente en términos de la base cartesiana. Por otra parte, como se ha tomado el eje $O Z$ paralelo a ambos conductores, y éstos se consideran de longitud infita, el campo magnético resultante en cualquier punto del espacio va a presentar las siguientes propiedades: es perpendicular a dicho eje, y sus componentes no van a ser función de la coordenada “ $z$ ”

$\Delta_1\!\ \|\!\ \vec{k}\!\ \| \Delta_2 \;\Longrightarrow\; \vec{B}_1(P)\perp\vec{k}\perp\vec{B}_2(P)\;\Longrightarrow\; \vec{B}(P)=B_x(x,y)\ \vec{\imath}\ + \ B_y(x,y)\ \vec{\jmath}\perp \vec{k}$

Es decir, la distribución del campo magnético es idéntica en todos los planos paralelos al plano 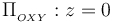$\Pi_{{}_{OXY}}:z=0$ . Por tanto, obtendremos dicho campo en un plano paralelo a aquél, donde todos los puntos tienen igual valor (arbitrario) en la coordenada “ $z$ ”. Por otra parte, nuestro interés se centra en los puntos del plano $\Pi_{{}_{OYX}}$ , con coordenada $x = 0$ , y para los que el valor de la coordenada “ $y$ ” puede expresarse en función de la distancia fija $\displaystyle a$ que separa los conductores del plano de simetría $\Pi_{{}_{OYZ}}$ , y la distancia variable $ρ$ existente entre un punto $P (0, y, z)$ de dicho plano y los conductores; como ya se discutió, esta distancia $ρ$ es idéntica para ambos conductores. Recuérdese que el módulo de los campos magnéticos creados por cada una de las corrientes es función de dicha distancia:

$P(0,y,z)\in\Pi_{{}_{OYZ}}\,\Longrightarrow\;\rho=\sqrt{a^2+y^2}\mathrm{,}\,\;\;\,\mathrm{tal}\,\,\,\mathrm{que}\,\;\;|\vec{B}_i(0,y,z)|=\frac{\mu_0\!\ |I_i|}{2\pi\!\ \rho}=B_i(\rho)$

Analicemos los dos supuestos planteados en el enunciado:

2.1 Caso de corrientes estacionarias antiparalelas

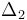
Consideramos el caso en que las corrientes que recorren los conductores filiformes son antiparalelas. Para la disposición de los amperímetros especificada en el enunciado, en el conductor $\displaystyle \Delta_1$ la intensidad de corriente es positiva, y negativa la soportada por el conductor $\displaystyle \Delta_2$

$\displaystyle I_1=I_0=-I_2>0$

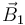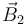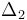En la figura se muestra la orientación de los campos $\vec{B}_1$ y $\vec{B}_2$ en el punto $P (0, y, z)$ , de acuerdo con la discusión realizada anteriormente: el primero “gira” en sentindo antihorario en torno a $\displaystyle \Delta_1$ , mientras que el segundo lo hace en sentido horario en torno a $\displaystyle \Delta_2$ .

Sea $\varphi$ el ángulo que forma el plano $\displaystyle \Pi_{{}_{OXZ}}$ sendos planos que contienen al punto $P (0, y, z)$ y a cada uno de los conductores rectilíneos. Se cumplirá:

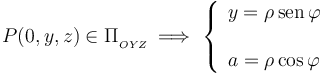
$P(0,y,z)\in\Pi_{{}_{OYZ}}\,\Longrightarrow\,\,\left\{ \begin{array}{l}\displaystyle y=\rho\,\mathrm{sen}\,\varphi\\ \\ \displaystyle a=\rho\cos\varphi\end{array}\right.$

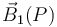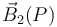Se puede comprobar que ambos campos $\vec{B}_1(P)$ y $\vec{B}_2(P)$ forman idéntico ángulo $\varphi$ con el plano paralelo al $\displaystyle \Pi_{{}_{OXZ}}$ que contiene al punto $P (0, y, z)$ , pero cada uno a un lado de dicho plano (véase la figura). Por tanto,

$\begin{array}{l}\displaystyle \vec{B}_1(0,y,z)=B_1(\rho)\!\ \bigg( -\mathrm{sen}\,\varphi\ \vec{\imath}\!\ +\!\ \cos\varphi\ \vec{\jmath}\!\ \bigg)=\frac{\mu_0\!\ I_0}{2\pi\!\ \rho} \bigg( -\mathrm{sen}\,\varphi\ \vec{\imath}\!\ +\!\ \cos\varphi\ \vec{\jmath}\!\ \bigg) \\ \\ \displaystyle \vec{B}_2(0,y,z)=B_2(\rho)\!\ \bigg(\mathrm{sen}\,\varphi\ \vec{\imath}\!\ +\!\ \, \cos\varphi\ \vec{\jmath}\!\ \bigg)=\frac{\mu_0\!\ I_0}{2\pi\!\ \rho} \bigg(\mathrm{sen}\,\varphi\ \vec{\imath}\!\ +\!\ \, \cos\varphi\ \vec{\jmath}\!\ \bigg) \end{array}$

Por tanto, el campo magnético resultante en los puntos del plano $\Pi_{{}_{OYZ}}$ es:

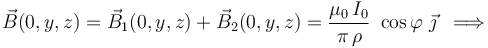
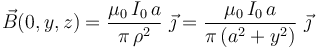
$\vec{B}(0,y,z)=\vec{B}_1(0,y,z)+\vec{B}_2(0,y,z)=\frac{\mu_0\!\ I_0}{\pi\!\ \rho}\ \cos\varphi\ \vec{\jmath}\;\;\Longrightarrow$ $\vec{B}(0,y,z)=\frac{\mu_0\!\ I_0\!\ a}{\pi\!\ \rho^2}\ \vec{\jmath}=\frac{\mu_0\!\ I_0\!\ a}{\pi\!\ (a^2+y^2)}\ \vec{\jmath}$

Obsérvese que el campo magnetico resultante en todos los puntos de dicho plano tiene la dirección del eje $O Y$ , con el sentido del vector unitario $\vec{\jmath}$ . Es decir,

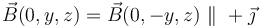
$\vec{B}(0,y,z)=\vec{B}(0,-y,z)\ \|\ +\vec{\jmath}$

2.2 Caso de corrientes estacionarias paralelas

Consideramos el caso en que las corrientes que recorren los conductores filiformes son paralelas, ambas negativas (es decir, recorren los conductores en sentido de la “ $z$ ” decreciente):

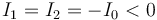
$\displaystyle I_1=I_2=-I_0<0$

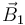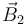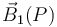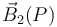En la figura se muestra la orientación de los campos $\vec{B}_1$ y $\vec{B}_2$ en el punto $P (0, y, z)$ , para esta nueva configuración de las corrientes. Ambos “giran” en sentido horario en torno a sus correspondientes corrientes rectilíneas. Utilizando de nuevo el ángulo $\varphi$ definido en el apartado anterior se observa que, en el punto $P (0, y, z)$ , los campos $\vec{B}_1(P)$ y $\vec{B}_2(P)$ se encuentran ambos al mismo lado del plano $\Pi_{{}_{OYZ}}$ , formando idéntico ángulo $\varphi$ con éste (ver figura). Las expresiones analíticas de estos campos es:

$\begin{array}{l}\displaystyle \vec{B}_1(0,y,z)=B_1(\rho)\!\ \bigg( \mathrm{sen}\,\varphi\ \vec{\imath}\!\ -\!\ \cos\varphi\ \vec{\jmath}\!\ \bigg)=\frac{\mu_0\!\ I_0}{2\pi\!\ \rho} \bigg( \mathrm{sen}\,\varphi\ \vec{\imath}\!\ -\!\ \cos\varphi\ \vec{\jmath}\!\ \bigg) \\ \\ \displaystyle \vec{B}_2(0,y,z)=B_2(\rho)\!\ \bigg(\mathrm{sen}\,\varphi\ \vec{\imath}\!\ +\!\ \, \cos\varphi\ \vec{\jmath}\!\ \bigg)=\frac{\mu_0\!\ I_0}{2\pi\!\ \rho} \bigg(\mathrm{sen}\,\varphi\ \vec{\imath}\!\ +\!\ \, \cos\varphi\ \vec{\jmath}\!\ \bigg) \end{array}$

Y teniendo en cuenta que 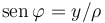$\displaystyle \mathrm{sen}\,\varphi=y/\rho$ , se obtiene la expresión para el campo magnético resultante en los puntos del plano $\Pi_{{}_{OYZ}}$ :

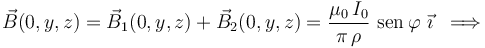
$\vec{B}(0,y,z)=\vec{B}_1(0,y,z)+\vec{B}_2(0,y,z)=\frac{\mu_0\!\ I_0}{\pi\!\ \rho}\ \mathrm{sen}\,\varphi\ \vec{\imath}\;\;\Longrightarrow$ $\vec{B}(0,y,z)=\frac{\mu_0\!\ I_0\!\ y}{\pi\!\ \rho^2}\ \vec{\imath}=\frac{\mu_0\!\ I_0\!\ y}{\pi\!\ (a^2+y^2)}\ \vec{\imath}$

Obsérvese que, en este caso, el campo magnetico resultante en los puntos de dicho plano tiene la dirección del eje $O X$ , con el sentido del unitario $\vec{\imath}$ en los puntos donde $y > 0$ , y sentido opuesto en $y < 0$ . El campo magnético es nulo si particularizamos en los puntos del eje $O Z$ , donde también se cumple $y = 0$ :

$\begin{array}{l}\displaystyle \vec{B}(0,y,z)=-\vec{B}(0,-y,z)\ \|\ +\vec{\imath}\;\;\;\;(y>0)\\ \\ \displaystyle \vec{B}(0,0,z)=\vec{0}\end{array}$

Campo magnético en el plano de simetría de dos corrientes filiformes rectilíneas (GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Caso de corrientes estacionarias antiparalelas

2.2 Caso de corrientes estacionarias paralelas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES