Campo magnético de una corriente filiforme rectilínea (F2GIA)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Campo magnético de la corriente filiforme rectilínea

1 Enunciado

Obténgase el campo magnético creado por una corriente estacionaria de intensidad $I 1$ que recorre una conductor rectilíneo de sección despreciable (filiforme) y de longitud indefinida.

2 Solución

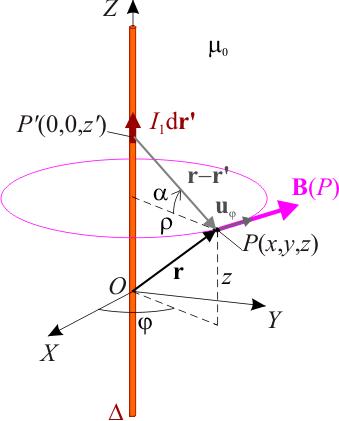
Consideremos una corriente eléctrica estacionaria de intensidad $I 1$ , que recorre un hilo conductor rectilíneo, $Δ$ , de longitud indefinidad, cuya sección puede considerarse despreciable; es decir, se trata de un conductor filiforme. Para describir analíticamente el espacio y las magnitudes físicas vectoriales, adotparemos un sistema de referencia cuyo eje $O Z$ coindice con el hilo de corriente. Obsérvese que al tener éste longitud indefinida, cualquiera de sus puntos puede ser considerado origen $O$ del sistema de referencia.

Una vez hecha la elección, un elemento de corriente 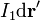$I_1\mathrm{d}\mathbf{r'}$ y su posición en un punto arbitrario del hilo, $P'$ , estarán descritos por los vectores:

$\overrightarrow{OP'}=\mathbf{r'}=z'\!\ \mathbf{k}\,\mathrm{;}\qquad\,I_1\mathrm{d}\mathbf{r'}=I_1\mathrm{d}z'\!\ \mathbf{k}$

2.1 Campo magnético de la corriente filiforme rectilínea

Para determinar el campo magnético creado por dicha corriente aplicaremos la ley de Biot y Savart. Sea un punto cualquiera del espacio, de coordenadas cartesianas $P (x, y, z)$ , cuya posición respecto del punto $O$ y respecto de la posición arbitraria de un elemento de corriente, viene dada por sendos vectores:

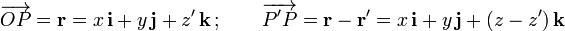
$\overrightarrow{OP}=\mathbf{r}=x\!\ \mathbf{i}+y\!\ \mathbf{j}+z'\!\ \mathbf{k}\,\mathrm{;}\qquad\,\overrightarrow{P'P}=\mathbf{r}-\mathbf{r'}=x\!\ \mathbf{i}+y\!\ \mathbf{j}+(z-z')\!\ \mathbf{k}$

El elemento de corriente 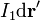$I_1\mathrm{d}\mathbf{r'}$ produce una contribución infinitesimal al campo magnético en el punto $P$ :

$\mathrm{d}\mathbf{B}\big\rfloor_P=\frac{\mu_0}{4\pi}\ \frac{I_1\mathrm{d}\mathbf{r'}\times (\mathbf{r}-\mathbf{r'})}{|\mathbf{r}-\mathbf{r'}|^3}=\frac{\mu_0 \!\ I_1}{4\pi}\ \frac{(-y\!\ \mathbf{i}+x\!\ \mathbf{j})\!\ \mathrm{d}z'}{\left[x^2+y^2+(z-z')^2\right]^{3/2}}$

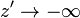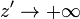En virtud del principio de superposición, el campo magnético total en el punto $P$ será igual a la suma de las contribuciones de todos los elementos de corriente en el hilo $Δ$ , desde $z'\rightarrow -\infty$ hasta $z'\rightarrow +\infty$ :

$\mathbf{B}(P)=\int_\Delta\!\mathrm{d}\mathbf{B}=\frac{\mu_0 \!\ I_1\big(-y\!\ \mathbf{i}+x\!\ \mathbf{j}\big)}{4\pi}\ \int_{-\infty}^\infty\!\frac{\!\ \mathrm{d}z'}{\left[x^2+y^2+(z-z')^2\right]^{3/2}}$

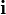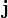Las coordenadas $x$ e $y$ del punto $P$ donde se evalúa el campo son independientes de la variable de integración $z'$ , y que los unitarios $\mathbf{i}$ y $\mathbf{j}$ de las coordenadas cartesianas son vectores constantes en todo el espacio. Por tanto, el vector 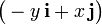$\big(-y\!\ \mathbf{i}+x\!\ \mathbf{j}\big)$ puede salir de la integral, indicando la dirección del campo magnético en dicho punto. Obsérvese que este vector es tangente en $P$ a una circunferencia centrada en el eje $O Z$ y contenida en el plano perpendicular a dicho eje. El radio de esta circunferencia es la distancia $ρ$ que hay entre el conductor rectilíneo y el punto $P$ ; y si denominamos $\varphi$ al ángulo que forma el plano $O X Z$ con el “vertical” que contiene al punto $P$ , se tendrán las siguientes relaciones entre las coordenadas y estas variables geométricas:

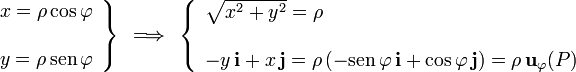
$\left.\begin{array}{l}x=\rho\cos\varphi\\ \\ y=\rho\,\mathrm{sen}\,\varphi\end{array}\right\}\;\,\Longrightarrow\;\,\left\{\begin{array}{l}\sqrt{x^2+y^2}=\rho\\ \\ \displaystyle -y\!\ \mathbf{i}+x\!\ \mathbf{j}=\rho\left(-\mathrm{sen}\,\varphi\!\ \mathbf{i}+\cos\varphi\!\ \mathbf{j}\right)=\rho\!\ \mathbf{u}_\varphi(P)\end{array}\right.$

Por otra parte, para calcular la anterior integral resulta muy conveniente realizar un cambio de variable en términos del ángulo $α$ que se indica en la figura:

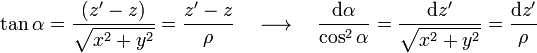
$\,\mathrm{tan}\,\alpha=\frac{(z'-z)}{\sqrt{x^2+y^2}}=\frac{z'-z}{\rho}\quad\longrightarrow\quad\frac{\mathrm{d}\alpha}{\cos^2\alpha}=\frac{\mathrm{d}z'}{\sqrt{x^2+y^2}}=\frac{\mathrm{d}z'}{\rho}$

Teniendo en cuenta que los límites de integración para esta variable son 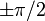$\pm\pi/2$ , se obtiene el valor del campo magnético en el punto $P$ . Y como éste es un punto arbitrario del espacio, obtenemos la expresión del campo magnético creado por el hilo rectilíneo y de longitud indefinida, tanto en coordenadas cartesianas como en términos de las variables $ρ$ y $\varphi$ (coordenadas polares en cada plano con valor de $z$ constante):

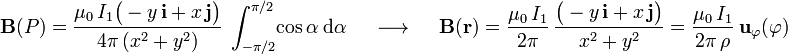
$\mathbf{B}(P)=\frac{\mu_0 \!\ I_1\big(-y\!\ \mathbf{i}+x\!\ \mathbf{j}\big)}{4\pi\left(x^2+y^2\right)}\ \int_{-\pi/2}^{\pi/2}\!\cos\alpha\ \mathrm{d}\alpha\quad\;\longrightarrow\quad\;\mathbf{B}(\mathbf{r})=\frac{\mu_0 \!\ I_1}{2\pi}\ \frac{\big(-y\!\ \mathbf{i}+x\!\ \mathbf{j}\big)}{x^2+y^2}=\frac{\mu_0 \!\ I_1}{2\pi\!\ \rho}\ \mathbf{u}_\varphi(\varphi)$

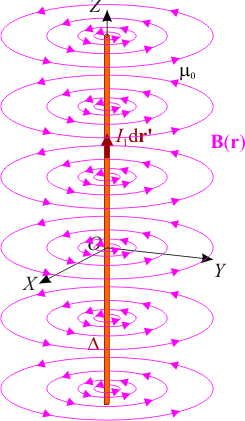
Como puede comprobarse, la magnitud del campo magnético en un punto es inversalmente proporcional a la distancia que lo separa del hilo rectilíneo de corriente, y en cada punto del espacio tiene la dirección tangente a la circunferencia centrada en el hilo y contenida en el plano perpendicular a éste. El conjunto de estas circunferencias concéntricas en distintos planos “horizontales”, constituyen las líneas del campo magnético creado por dicha corriente.

Campo magnético de una corriente filiforme rectilínea (F2GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Campo magnético de la corriente filiforme rectilínea

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES