Primera Prueba de Control 2012/13 (F1 G.I.A.)
De Laplace
Contenido |
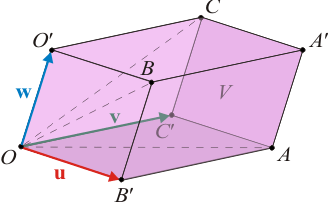
1 Posición de vértices y volumen de un paralelepípedo
Los puntos O, A, B y C son vértices no contiguos de un paralelepípedo, de manera que O y A se encuentran en un plano distinto al que contiene a B y C. Las coordenadas de estos puntos en un sistema dereferencia cartesiano son:
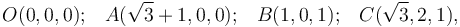
medidas en unidades de longitud. Determine las componentes cartesianas de los vectores
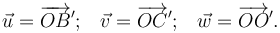
y calcule el volumen del paralelepípedo.
2 Movimiento instantáneo de una partícula
Una partícula P se mueve respecto de un sistema de referencia cartesiano OXYZ de manera que en un cierto instante t0, su velocidad  y su aceleración
y su aceleración  están descritas, respectivamente, por los vectores
están descritas, respectivamente, por los vectores
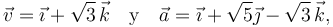
con sus componentes medidas en m / s2. Determine, en el instante considerado, las siguientes magnitudes cinemáticas:
- Módulo de la velocidad (celeridad) y su derivada.
- Componente normal de la aceleración y radio de curvatura de la trayectoria.
- Vector aceleración normal.
3 Partícula ensartada en aro horizontal
Una partícula P de masa m se mueve ensartada en un aro de radio R, contenido en el plano cartesiano OXY, y cuyo centro se encuentra en un punto de dicho plano, de coordenadas C(R,0,0). La partícula, que en el instante inicial (t = 0) se encuentra en el punto A de coordenadas A(2R,0,0), se mueve de manera que el ángulo que forma el radiovector
que forma el radiovector 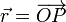 con el eje OX varía en el tiempo con velocidad angular constante,
con el eje OX varía en el tiempo con velocidad angular constante,
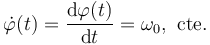
- Obtenga una expresión paramétrica de la trayectoria.
- Ley horaria para el módulo de la velocidad (celeridad).
- Componentes intrínsecas de la aceleración de la partícula.
- Fuerzas aplicadas sobre la partícula, expresadas en el triedro instrínseco, sabiendo que el plano OXY es perpendicular a la vertical gravitatoria definida por el vector gravedad
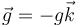 .
.
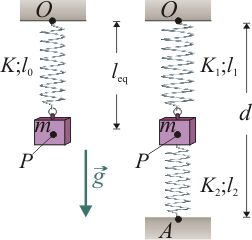
4 Sistema equivalente a dos resortes alineados
Una partícula pesada P de masa m, se halla en equilibrio por la acción de dos resortes, uno de constante recuperadora K1 y longitud natural l1, y otro de constante recuperadora K2 y longitud natural l2, tales que K1l1 = K2l2. El primer resorte tiene un extremo conectado a P y el otro a un punto fijo O; el segundo resorte se conecta a la partícula y a un punto fijo A, separado de O por una distancia d. En la situación de equilibrio, los puntos O, P y A están alineados en la dirección y el sentido de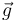 (gravedad). ¿Cuáles deben ser los valores de la constante K y la longitud natural l0 de un único resorte que conectado al punto O, produzca la misma situación de equilibrio que los dos resortes?
(gravedad). ¿Cuáles deben ser los valores de la constante K y la longitud natural l0 de un único resorte que conectado al punto O, produzca la misma situación de equilibrio que los dos resortes?