Problemas de dinámica de los sistemas de partículas (GIE)
De Laplace
1 Problemas de boletín
1.1 Centro de masas en sistemas de esferas
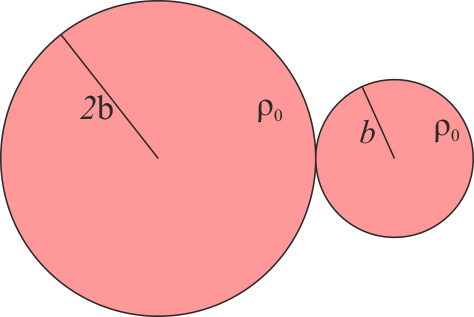
Se tienen dos esferas macizas del mismo material de densidad homogénea, ρ0, una de ellas de radio 2b y la otra de radio b. Las dos esferas son adyacentes. Determine la posición del centro de masas del sistema.
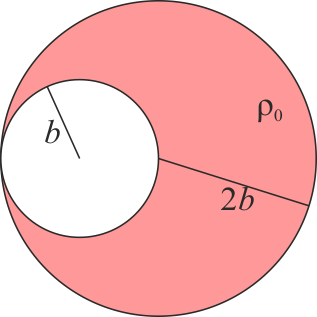
Si en lugar del sistema anterior se tiene una sola esfera maciza de radio 2b y densidad homogénea ρ0 en la que se ha horadado una cavidad también esférica, de radio b, cuyo centro se encuentra a una distancia R / 2 del centro de la esfera original ¿dónde se halla el centro de masas del sólido?
1.2 Centro de masas de cuatro partículas en un cuadrado
Se tienen 4 masas que ocupan los vértices de un cuadrado de lado 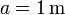 . Calcule la posición del centro de masas del sistema en cada uno de los casos siguientes
. Calcule la posición del centro de masas del sistema en cada uno de los casos siguientes
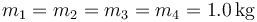 .
.
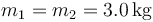 ,
, 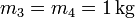 .
.
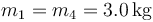 ,
, 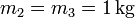 .
.
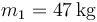 ,
,  .
.

1.3 Propiedades de un sistema de tres partículas
Considere un sistema de tres partículas de masas 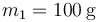 ,
, 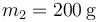 ,
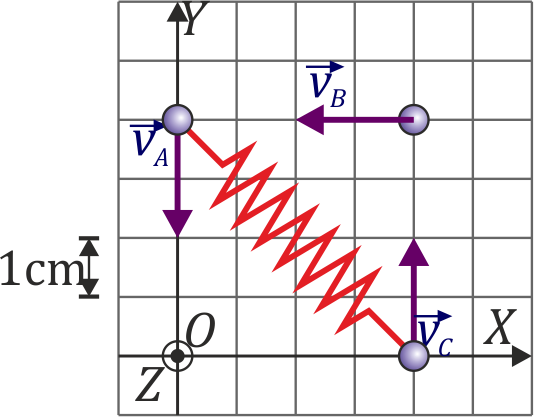
, 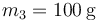 que en un instante dado están situadas en las posiciones de la figura y moviéndose con la velocidad indicada, siendo la rapidez de cada una de ellas
que en un instante dado están situadas en las posiciones de la figura y moviéndose con la velocidad indicada, siendo la rapidez de cada una de ellas  . Suponga
que la masa 1 y la 3 está unidas por un resorte de longitud natural nula y constante
. Suponga
que la masa 1 y la 3 está unidas por un resorte de longitud natural nula y constante 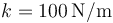 . Para el instante indicado
. Para el instante indicado
- Halle la posición del centro de masas (CM) del sistema.
- Calcule la cantidad de movimiento del sistema.
- Halle el momento cinético respecto al origen y respecto al CM.
- Calcule la energía cinética del sistema respecto a un sistema fijo y respecto al CM.
- Halle la aceleración de cada masa y la del CM.
- Halle la derivada respecto al tiempo del momento cinético (calculado respecto al origen).
- Calcule la derivada respecto al tiempo de la energía cinética del sistema (calculada respecto a un sistema fijo).
1.4 Propiedades de rotores descentrados
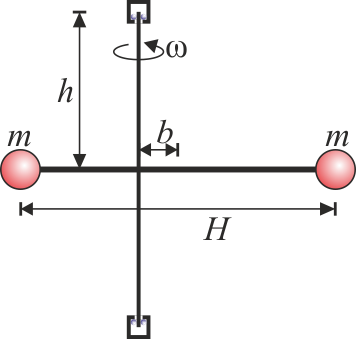
Se tiene un rotor formado por dos masas iguales de valor m situadas en los extremos de una barra ideal (sin masa) de longitud H. Cuando este rotor está equilibrado gira en torno a un eje perpendicular a la barra y que pasa por su centro. Este eje está anclado en dos rodamientos situados a una distancia h del centro de la barra (uno por encima y otro por debajo de ella).
Calcule el momento cinético y la energía cinética (respecto a un sistema fijo y respecto al CM) si el rotor gira con velocidad angular constante ω en torno al eje cuando:
- Es horizontal y se encuentra centrado en el eje vertical.
- Es horizontal pero se encuentra descentrado de forma que el eje no pasa por el centro de la barra, sino a una distancia b de éste.
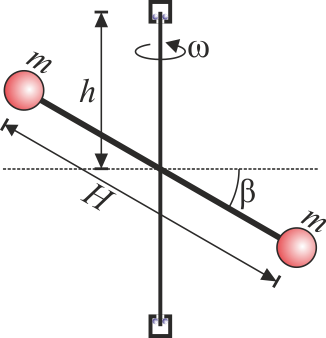
- Está centrado pero la barra está inclinada respecto a la horizontal un ángulo β.
- Es horizontal y se encuentra centrado en el eje vertical, pero las masas no son exactamente iguales, sino que valen m1 y m2.
1.5 Magnitudes en una máquina de Atwood
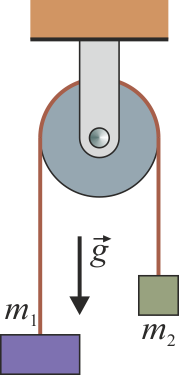
Considere una máquina de Atwood ideal formada por dos masas m1 y m2 que cuelgan de una polea (ideal, sin rozamiento ni masa) de radio b a través de un hilo también ideal (inextensible y sin masa) de longitud l). Inicialmente las dos masas están en reposo a la misma altura.
- Determine la masa total, la posición, velocidad y aceleración del centro de masas, la cantidad de movimiento, el momento cinético respecto al centro de la polea y la energía cinética del sistema, todo ello como función del tiempo.
- Para la cantidad de movimiento, el momento cinético respecto al centro de la polea y la energía cinética determine sus derivadas respecto al tiempo y comprueba que se satisfacen las leyes para su evolución.
1.6 Magnitudes en un sistema de dos masas y un hilo
Repita los dos apartados del problema anterior si en lugar de dos masas que cuelgan verticalmente tenemos una masa m1 que desliza sin rozamiento por una mesa horizontal y una masa m2 que cuelga verticalmente, estando unidas por un hilo ideal que pasa por una polea también ideal, situada en el borde de la mesa.
1.7 Colisión parcialmente inelástica
Una partícula de masa m1 y que se mueve con velocidad v0 impacta frontalmente con una de masa m2 que se encuentra en reposo. El coeficiente de restitución vale CR = 0.5
- Halle las velocidades finales de las dos partículas
- Calcule la cantidad de energía cinética disipada en el proceso.
- ¿A qué tienden los resultados anteriores si
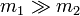 ? ¿Y si
? ¿Y si 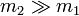 ?
?
1.8 Cañón casero
Se puede construir un sencillo cañón casero para disparos en vertical de la siguiente manera: se toma un tubo vertical de longitud L (tómese 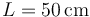 ) cuyo extremo inferior se apoya en el suelo. Por su interior se dejan caer prácticamente seguidas dos bolas, siendo la inferior mucho más pesada que la superior (por ejemplo, una bola de acero y una pelota de ping-pong). Estime la altura máxima a la que subiría la bola ligera tras los rebotes. Justifique las aproximaciones que se efectúen.
) cuyo extremo inferior se apoya en el suelo. Por su interior se dejan caer prácticamente seguidas dos bolas, siendo la inferior mucho más pesada que la superior (por ejemplo, una bola de acero y una pelota de ping-pong). Estime la altura máxima a la que subiría la bola ligera tras los rebotes. Justifique las aproximaciones que se efectúen.
1.9 Péndulo balístico
Un péndulo balístico es un dispositivo elemental para determinar la velocidad de un proyectil. Consiste en un bloque pesado de madera, de masa M que pende de un hilo de longitud L. Sobre este bloque, inicialmente en reposo, impacta una bala de masa m que se mueve, justo antes del impacto, con velocidad v0, quedándose empotrada en el bloque. Determine el ángulo máximo de desviación del péndulo respecto a la vertical. Si lo que se mide es el ángulo, obtenga una expresión para la velocidad de impacto.
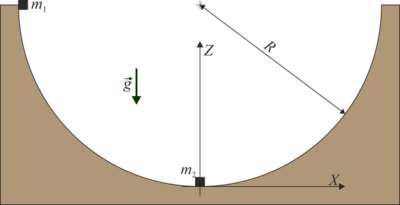
1.10 Colisión en el interior de un cuenco
En el interior de un cuenco hemisférico de radio 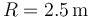 cuyo borde es horizontal, se encuentran dos partículas que pueden deslizar sin rozamiento por su superficie. Una de ellas, de masa
cuyo borde es horizontal, se encuentran dos partículas que pueden deslizar sin rozamiento por su superficie. Una de ellas, de masa 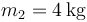 , se encuentra en reposo en el fondo del cuenco. La otra, de masa
, se encuentra en reposo en el fondo del cuenco. La otra, de masa 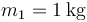 se coloca en el borde del cuenco y desde allí se suelta.
se coloca en el borde del cuenco y desde allí se suelta.
- Calcule, con justificación, la velocidad que lleva la masa 1 justo antes de impactar con la masa 2. Halle la reacción del cuenco sobre la masa 1 para el mismo instante.
- Si el choque es perfectamente elástico, calcule las velocidades de las dos masas justo tras la colisión.
- Para este caso elástico, halle la altura máxima desde el fondo del cuenco que alcanza cada una de las masas tras el choque.
- Repita los dos apartados anteriores para el caso de que la colisión sea completamente inelástica. ¿Cuánta energía se pierde en la colisión en ese caso?
Tómese g = 9.8m/s²
1.11 Colisión elástica en el plano
Una partícula de masa  que se mueve con velocidad
que se mueve con velocidad 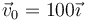 (m/s) colisiona elásticamente con un blanco de la misma masa, que se encuentra en reposo en el origen de coordenadas. Tras la colisión, el blanco se mueve con una rapidez de 28 m/s. Calcule, para el instante posterior a la colisión:
(m/s) colisiona elásticamente con un blanco de la misma masa, que se encuentra en reposo en el origen de coordenadas. Tras la colisión, el blanco se mueve con una rapidez de 28 m/s. Calcule, para el instante posterior a la colisión:
- La rapidez del proyectil.
- El ángulo que forman las velocidades.
- La velocidad de cada partícula.
1.12 Colisión inelástica en el plano
Un neutrón de masa m que se mueve con velocidad 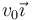 choca con un protón (de casi la misma masa), que se mueve con velocidad
choca con un protón (de casi la misma masa), que se mueve con velocidad 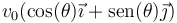 . La colisión es completamente inelástica, de forma que tras ella, las dos partículas se mueven solidariamente como un núcleo de deuterio. La colisión se produce en el origen de coordenadas.
. La colisión es completamente inelástica, de forma que tras ella, las dos partículas se mueven solidariamente como un núcleo de deuterio. La colisión se produce en el origen de coordenadas.
- ¿Cuál es la velocidad final de la nueva partícula formada? ¿Qué ángulo forma con el eje OX?
- ¿Cuánta energía se pierde en la colisión? ¿Para qué valores de θ es máxima o mínima esta energía perdida?
2 Problemas adicionales
2.1 Variación de la presión atmosférica
La presión atmosférica en un punto se debe al peso por unidad de superficie de la columna de aire situada sobre él. En un modelo de la atmósfera, se supone que la densidad del aire disminuye con la altura como

extendiéndose la altura hasta el infinito.
- Determine el peso del aire situado por encima de un cuadrado de lado L situado a una altura z0 sobre el nivel del mar. A partir de aquí halle como varía la presión atmosférica con la altura.
- Sabiendo que al nivel del mar la presión es de 101325 Pa y la densidad del aire es de 1.225 kg/m³, calcule el valor de la constante α.
- Usando esta fórmula halle el valor de la presión atmosférica en La Paz, situada a 3650 m de altitud.
- Halle el valor aproximado de la masa de aire de la atmósfera.
En todos los pasos, razone los cálculos y justifique las aproximaciones que se hagan.
2.2 Masa de esfera no homogénea
Se tiene una distribución de masa con simetría esférica, con una densidad dependiente de la posición tal que
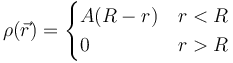
siendo  la distancia al centro de la esfera. Halle la masa total de la esfera.
la distancia al centro de la esfera. Halle la masa total de la esfera.
2.3 Masa arrastrada sobre una mesa
Se tiene un sistema de 2 masas de 4 kg cada una, atadas por una cuerda ideal, inextensible y sin masa, que pasa por una polea también ideal. La masa 1 está sobre una superficie horizontal sin rozamiento, mientras que la 2 cuelga verticalmente.
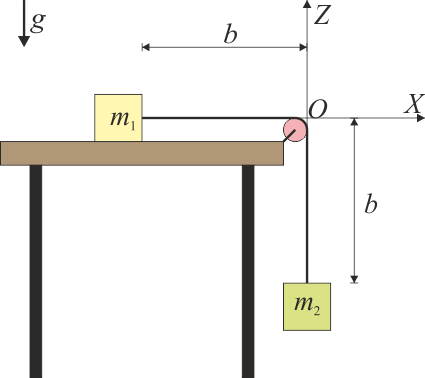
Empleando el sistema de ejes de la figura y para el instante reflejado en ella:
- ¿Cuál es la aceleración de cada una de las masas?
- ¿Dónde se halla el centro de masas?
- ¿Cuál es la aceleración del CM?
- Si en el isntante representado la masa 1 tiene una rapidez v0, ¿cuánto vale la velocidad del CM?
- Para el caso de apartado anterior, ¿cuánto valen la cantidad de movimiento, la energía cinética y el momento cinético respecto al origen y respecto al CM?
2.4 Dos partículas unidas por un oscilador armónico
Supongamos dos partículas de la misma masa m unidas por un resorte de constante k y longitud natural nula. Inicialmente ambas masas se encuentran en el mismo punto; estando ambas en reposo. Se le comunica a la partícula 2 una velocidad v0 alejándola de la primera. ¿Cuál es el movimiento subsiguiente de ambas partículas?
2.5 Ejemplo de sistema de tres partículas
Tres partículas puntuales se encuentran en un cierto instante en los vértices de un triángulo. Las masas, posiciones y velocidades de las partículas son,
| i | mi (g) | 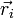 (m) (m)
| 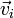 (m/s) (m/s)
|
|---|---|---|---|
| 1 | 400 | 
| 
|
| 2 | 500 | 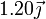
| 
|
| 3 | 300 | 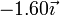
| 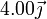
|
Las tres partículas están conectadas por resortes de longitud natural nula. No hay más fuerzas actuando en el sistema, siendo la constante de los que unen la masa 2 con la 1 y la 2 con la 3 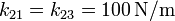 y el que une la 1 con la 3
y el que une la 1 con la 3  .
.
Para el instante indicado:
- Determine la aceleración de cada partícula.
- Calcule la posición, velocidad y aceleración del CM.
- Calcule el momento cinético del sistema respecto al origen y respecto al CM.
- Halle la energía cinética del sistema respecto al origen y respecto al CM.
- Calcule las derivadas respecto al tiempo de la cantidad de movimiento, del momento cinético y de la energía cinética.
2.6 Explosión de un proyectil
Con un mortero se lanza un proyectil de 3 kg con una rapidez de 100 m/s y una inclinación respecto a la horizontal del 75%. Cuando el proyectil se encuentra en el punto más alto de la trayectoria, se divide en dos fragmentos. Uno de ellos, de masa 1 kg adquiere en ese momento una velocidad 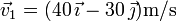 .
.
- Determine la velocidad del segundo fragmento justo tras la explosión.
- Calcule la variación de la energía cinética como consecuencia del estallido.
- Halle el punto de impacto de cada uno de los dos fragmentos.
- En el momento en que impacta el primer fragmento, ¿dónde se encuentra el centro de masas del sistema?
2.7 Propulsión con resorte
Sobre una mesa horizontal se encuentra un bloque de masa 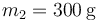 . Para lanzarlo por el plano se emplea un resorte de constante
. Para lanzarlo por el plano se emplea un resorte de constante  en cuyo extremo se encuentra una masa
en cuyo extremo se encuentra una masa 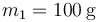 . En la posición de equilibrio, las dos masas se tocan. El resorte no tiene rozamiento alguno. La masa m2 tiene un coeficiente de rozamiento (estático y dinámico) μ = 0.2 con la mesa.
. En la posición de equilibrio, las dos masas se tocan. El resorte no tiene rozamiento alguno. La masa m2 tiene un coeficiente de rozamiento (estático y dinámico) μ = 0.2 con la mesa.
Se comprime el resorte una distancia 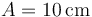 y a continuación se libera, para que golpee a la masa m2 y esta salga disparada.
y a continuación se libera, para que golpee a la masa m2 y esta salga disparada.
- Halle la velocidad que lleva la masa m1 en el momento del impacto.
- Suponiendo que el choque es elástico, calcule las velocidades que tienen las masas justo tras la colisión.
- Calcule la distancia recorrida por m2 hasta que se para y el tiempo que tarda en hacerlo.
- Halle cuánto se vuelve a contraer el muelle tras la colisión.

2.8 Colisión de dos péndulos
Se tienen dos péndulos ideales con barras rígidas de la misma longitud L y masa nula, que cuelgan del mismo punto O. Las masas sujetas a los extremos de los hilos son respectivamente m1 y m2. La masa m1 es elevada a una altura h1 y se suelta desde el reposo, colisionando con la masa m2 que se encuentra en el punto más bajo.
Suponiendo que la colisión es elástica, determina la altura a la que sube cada masa tras la colisión. Distingue los casos m1 > m2, m1 = m2 y m1 < m2.
¿Qué condiciones deben cumplirse para conseguir que la masa m2 gire y llegue hasta arriba del todo?
3 Preguntas de test
3.1 Colisión tridimensional
Una proyectil de masa m que se mueve con velocidad 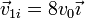 colisiona con un blanco inmóvil de masa 2m. El proyectil tiene tras la colisión una velocidad
colisiona con un blanco inmóvil de masa 2m. El proyectil tiene tras la colisión una velocidad 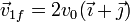 ¿Cuánto vale la velocidad final de la segunda masa?
¿Cuánto vale la velocidad final de la segunda masa?
- A
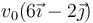 .
.
- B Es nula.
- C Depende de si la colisión es elástica o inelástica.
- D
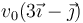 .
.
3.2 Arrastre de una masa
Se tiene un sistema de 2 masas de 4 kg cada una, atadas por una cuerda ideal, inextensible y sin masa, que pasa por una polea también ideal. La masa 1 está sobre una superficie horizontal sin rozamiento, mientras que la 2 cuelga verticalmente.

Suponiendo el sistema de ejes de la figura, ¿cuánto vale la aceleración de cada masa en el instante indicado, en m/s²?
- A
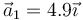 ,
, 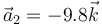
- B
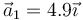 ,
, 
- C
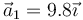 ,
, 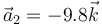
- D
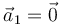 ,
, 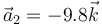
¿Cuál de las cuatro figuras representa correctamente la posición y velocidad del centro de masas C del sistema de dos pesas, en el instante representado?
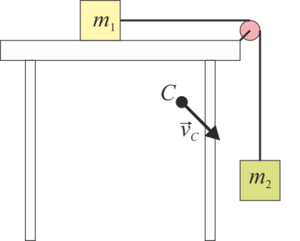
| 
|
| A | B |
|---|---|

| 
|
| C | D |
¿Cuánto vale la aceleración del centro de masas en el mismo instante?
- A
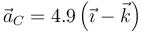
- B Es nula.
- C
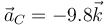
- D
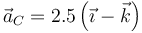
3.3 Centro de masas de una L
Se tiene un sólido en forma de L con los brazos de igual longitud h, siendo M la masa total del sólido, distribuida uniformemente.
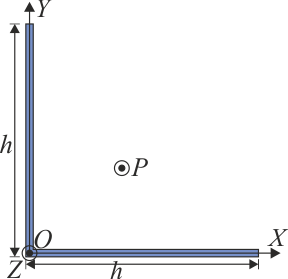
Considerando un sistema de ejes con origen en el vértice y ejes OX y OY paralelos a los brazos de la L, ¿dónde se encuentra en centro de masas del sólido?
- A En

- B En el origen de coordenadas.
- C En
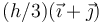
- D En
3.4 Impacto horizontal sobre un bloque
Para medir una velocidad de un proyectil se dispara una bala de masa 4 gramos sobre un bloque de madera de 1 kg, inicialmente en reposo, quedándose la bala empotrada en él. El bloque reposa sobre una superficie horizontal, sobre la cual el coeficiente de rozamiento (estático y dinámico) es μ = 0.25. Como consecuencia del impacto, el bloque (con bala) se desliza una distancia de 20 cm hasta pararse.
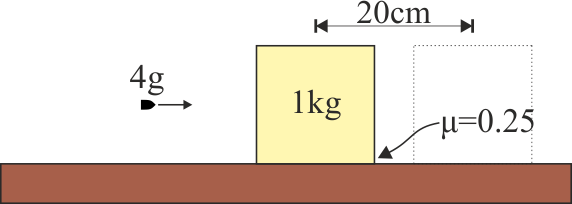
¿Qué velocidad tenía aproximadamente el bloque justo tras el impacto?
- A 2 m/s
- B 70 cm/s
- C 20 cm/s.
- D 1 m/s.
¿Qué velocidad llevaba la bala justo antes del impacto?
- A 500 m/s
- B 250 m/s
- C 50 m/s
- D 16 m/s
¿Qué proporción de la energía inicial se perdió en la colisión de la bala con el bloque?
- A 0.0%
- B 50.0%
- C 99.6%
- D 0.4%
3.5 Explosión de un proyectil
Un proyectil de masa 4 kg se mueve horizontalmente con velocidad de 6 m/s. En un momento dado explota en dos fragmentos, uno de los cuales tiene una masa de 1 kg y sale despedido hacia atrás con velocidad −6 m/s.
¿Cuál es la velocidad del segundo fragmento tras la explosión?
- A 18 m/s
- B 6 m/s
- C 0 m/s
- D 10 m/s
En este proceso la energía cinética del sistema…
- A Disminuye.
- B Permanece constante.
- C Cambia de signo.
- D Aumenta.
3.6 Superficies esféricas adyacentes
Con una chapa metálica rígida se construyen dos superficies esféricas, una de radio 2R y otra de radio R, que se colocan adyacentes. La masa total del sistema es M
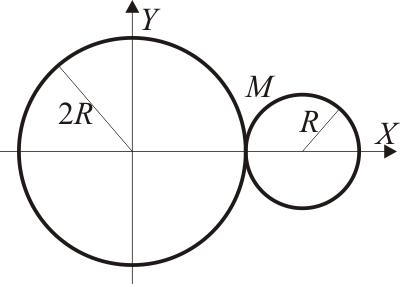
En el sistema de ejes de la figura, ¿dónde se encuentra el centro de masas del sistema?
- A
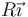
- B
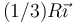
- C
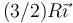
- D
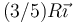
- A
3.7 Colisión de proyectil masivo
Una proyectil de 4 kg que se mueve a velocidad v0 choca contra un blanco de 1 kg, que estaba en reposo. Tras la colisión, ambas masas se mueven conjuntamente. ¿Qué proporción de la energía cinética se pierde en la colisión?
- A Depende del valor de v0
- B 80%
- C 20%
- D 0%
3.8 Centro de masas de una T
Se tiene un sólido en forma de T formado por dos varillas homogéneas de la misma densidad, siendo el travesaño de longitud 2h y el mástil de longitud h. La masa total del sólido es M
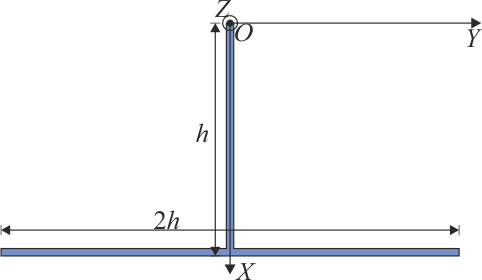
En el sistema de ejes de la figura, ¿dónde se encuentra el centro de masas del sistema?
- A

- B
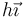
- C
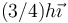
- D
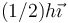
- A





