Colisión parcialmente inelástica

De Laplace

Contenido

1 Enunciado
2 Velocidades finales
3 Disipación de energía cinética
4 Límite de los resultados
- 4.1 Proyectil pesado
- 4.2 Blanco pesado

1 Enunciado

Una partícula de masa $m 1$ y que se mueve con velocidad $v 0$ impacta frontalmente con una de masa $m 2$ que se encuentra en reposo. El coeficiente de restitución vale $C R = 0.5$

Halle las velocidades finales de las dos partículas
Calcule la cantidad de energía cinética disipada en el proceso.
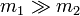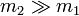¿A qué tienden los resultados anteriores si $m_1\gg m_2$ ? ¿Y si $m_2\gg m_1$ ?

2 Velocidades finales

Las velocidades finales las obtenemos de dos ecuaciones:

La conservación de la cantidad de movimiento: Suponiendo que tras el choque ambas partículas se mueven sobre la recta por la que venía el proyectil inicial, esta ley nos da

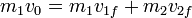
$m_1v_0 = m_1v_{1f}+m_2v_{2f}\,$

El coeficiente de restitución es conocido: Este coeficiente relaciona la velocidad relativa de alejamiento con la de acercamiento

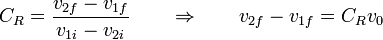
$C_R=\frac{v_{2f}-v_{1f}}{v_{1i}-v_{2i}}\qquad\Rightarrow\qquad v_{2f}-v_{1f}=C_Rv_0$

Estos da un sistema de dos ecuaciones con dos incógnitas, con solución general

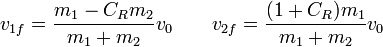
$v_{1f}=\frac{m_1-C_Rm_2}{m_1+m_2}v_0\qquad v_{2f}=\frac{(1+C_R)m_1}{m_1+m_2}v_0$

Esta fórmula es general y vale también para colisiones elásticas ( $C R = 1$ ) y completamente inelásticas ( $C R = 0$ ).

En el caso del enunciado en el que $C R = 1 / 2$ queda

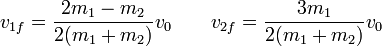
$v_{1f}=\frac{2m_1-m_2}{2(m_1+m_2)}v_0\qquad v_{2f}=\frac{3m_1}{2(m_1+m_2)}v_0$

3 Disipación de energía cinética

Como resultado de la colisión las partículas modifican su energía cinética. El proyectil pierde energía y el blanco la gana. El balance neto lo da la suma de los dos incrementos.

3.1 Variación para el proyectil

El incremento (que será negativo) de la energía cinética del proyectil es

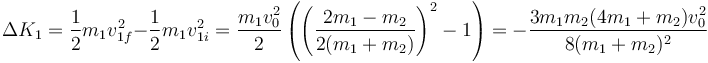
$\Delta K_1 = \frac{1}{2}m_1v_{1f}^2-\frac{1}{2}m_1v_{1i}^2 = \frac{m_1v_0^2}{2}\left(\left(\frac{2m_1-m_2}{2(m_1+m_2)}\right)^2-1\right)= -\frac{3m_1m_2(4m_1+m_2)v_0^2}{8(m_1+m_2)^2}$

3.2 Variación para el blanco

Operando igualmente para la masa 2

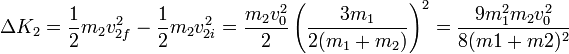
$\Delta K_2 = \frac{1}{2}m_2v_{2f}^2-\frac{1}{2}m_2v_{2i}^2 = \frac{m_2v_0^2}{2}\left(\frac{3m_1}{2(m_1+m_2)}\right)^2=\frac{9m_1^2m_2v_0^2}{8(m1+m2)^2}$

3.3 Balance neto

Sumando los dos incrementos queda la variación neta

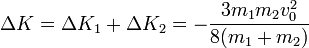
$\Delta K = \Delta K_1+\Delta K_2 = -\frac{3m_1m_2v_0^2}{8(m_1+m_2)}$

En comparación con la energía cinética inicial, la disipación de energía es igual a

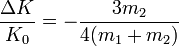
$\frac{\Delta K}{K_0}=-\frac{3m_2}{4(m_1+m_2)}$

4 Límite de los resultados

4.1 Proyectil pesado

Cuando el proyectil es mucho más pesado que el blanco (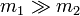 $m_1\gg m_2$ ), en las expresiones se puede despreciar $m 2$ comparado con $m 1$ en las sumas o restas, lo que reduce los resultados a

$v_{1f}\to v_0\qquad v_{2f}\to\frac{3}{2}v_0$

esto es, el proyectil sigue con la misma velocidad que llevaba, mientras que el blanco se aleja con un 50% más de velocidad (frente al doble de velocidad, con el que sale en el caso elástico).

Las variaciones de energía cinética en este límite son

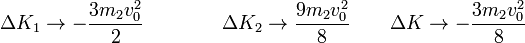
$\Delta K_1 \to -\frac{3m_2v_0^2}{2}\qquad \qquad \Delta K_2 \to \frac{9m_2v_0^2}{8}\qquad \Delta K \to -\frac{3m_2v_0^2}{8}$

Obsérvese que aunque la velocidad del proyectil disminuye una cantidad despreciable, su energía cinética disminuye una cantidad finita.

En proporción

$\frac{|\Delta K_2|}{|\Delta K_1|}=\frac{3}{4}\qquad\qquad \frac{|\Delta K|}{|\Delta K_1|}=\frac{1}{4}$

esto es, de lo que disminuye la energía cinética del proyectil, un 75% se va en aumento de la energía cinética del blanco y un 25% se pierde (usualmente en forma de calor).

4.2 Blanco pesado

Cuando el proyectil es mucho más ligero que el blanco (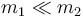 $m_1\ll m_2$ ), en las expresiones se puede despreciar $m 1$ comparado con $m 2$ en las sumas o restas, lo que reduce los resultados a

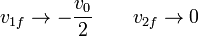
$v_{1f}\to -\frac{v_0}{2}\qquad v_{2f}\to0$

esto es, el proyectil rebota con la mitad de la velocidad con la que impactó, mientras que el blanco masivo permanece en reposo. Este es el ejemplo típico de una pelota no completamente elástica que rebota con el suelo

Las variaciones de energía cinética en este límite son

$\Delta K_1 \to -\frac{3m_1v_0^2}{8}\qquad \qquad \Delta K_2 \to 0\qquad\qquad \Delta K \to -\frac{3m_1v_0^2}{8}$

En proporción

$\frac{|\Delta K_2|}{|\Delta K_1|}=0\qquad\qquad \frac{|\Delta K|}{|\Delta K_1|}=1$

esto es, todo lo que disminuye la energía cinética del proyectil se pierde en la colisión. La energía perdida, según el resultado del primer apartado, es el 75% de la energía cinética inicial.

Colisión parcialmente inelástica

De Laplace

Contenido

1 Enunciado

2 Velocidades finales

3 Disipación de energía cinética

3.1 Variación para el proyectil

3.2 Variación para el blanco

3.3 Balance neto

4 Límite de los resultados

4.1 Proyectil pesado

4.2 Blanco pesado

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES