Problemas de corriente eléctrica (GIE)
De Laplace
1 Velocidad de arrastre en un hilo de plata
Halle la velocidad de arrastre de los electrones en un cable de plata de 0.5 mm² de sección por el cual circula una corriente de 100 mA.
2 Cable bimetálico
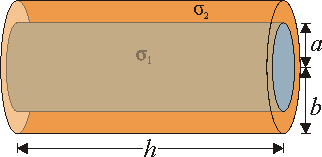
Entre los distintos tipos de cable empleados en la industria, se encuentra el de acero revestido de cobre. Está formado por un núcleo de acero de radio a (suponga 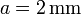 ), rodeado por una capa de cobre, de radio exterior b (sea
), rodeado por una capa de cobre, de radio exterior b (sea 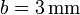 ).
).
- Calcule la resistencia de un cable de esta clase de longitud
 .
.
- Determine la intensidad de corriente que circula por cada metal cuando se aplica una diferencia de potencial
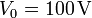 al cable anterior.
al cable anterior.
Datos: 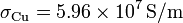 ,
, 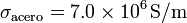
3 Resistividad dependiente de la posición
Tras una rotura de un cable de cobre (de resistividad r1) de sección S y gran longitud, se procede a unir los dos pedazos mediante una soldadura. Como consecuencia de la presencia de óxido la resistividad del cable aumenta hasta un valor r2 en una región alrededor del punto de contacto, pudiéndose describir matemáticamente según la ley
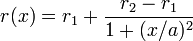
Calcule el aumento de la resistencia total del cable. Aplíquese al caso  ,
, 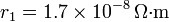 ,
, 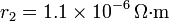 ,
, 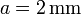 .
.
4 Paso de un pulso de corriente
Por un hilo rectilíneo de gran longitud y resistencia eléctrica R1 circula una corriente variable en el tiempo, tal que su valor es
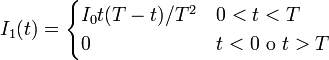
- Halle la carga que pasa por un punto del hilo entre
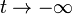 y
y 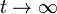 .
.
- Calcule la energía disipada en el cable en el mismo tiempo.
5 Asociación de dos bombillas en serie
Se colocan en serie dos bombillas de potencias nominales 100 W y 60 W y se conectan a la red. Si la potencia radiada es proporcional a la potencia consumida, ¿cuál de las dos bombillas darán más luz? ¿En qué proporción?
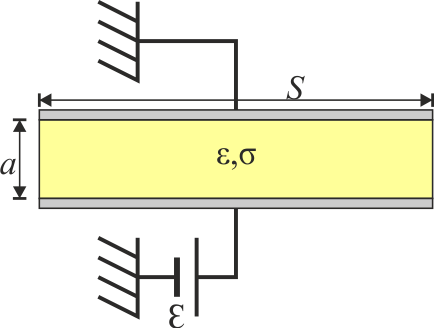
6 Condensador con pérdidas
En un modelo de condensador real (“con pérdidas”) se tienen dos placas paralelas perfectamente conductoras de sección S, separadas una distancia a entre las cuales hay un dieléctrico de permitividad  y con una pequeña conductividad σ. Entre las placas se establece una d.d.p. constante por medio de una fuente de f.e.m
y con una pequeña conductividad σ. Entre las placas se establece una d.d.p. constante por medio de una fuente de f.e.m 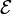 .
.
- Calcule el campo eléctrico y la densidad de corriente entre las placas.
- Halle la energía almacenada en el sistema y la potencia consumida en el dispositivo.
- Diseñe el circuito equivalente a este dispositivo.
- Si la fuente que alimenta a este elemento es una fuente real con f.e.m.
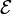 y resistencia interna r, ¿cuánto valen en ese caso la carga, la corriente, la energía y la potencia?
y resistencia interna r, ¿cuánto valen en ese caso la carga, la corriente, la energía y la potencia?
- Si la d.d.p. que se aplica entre las placas no es continua, sino que varía como V(t), ¿qué corriente llega por el cable al dispositivo?
- ¿Qué ocurre si se desconecta la fuente?
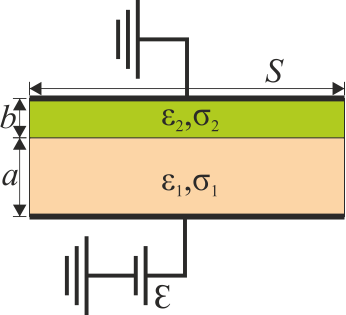
7 Condensador con dos capas no ideales
Entre dos placas perfectamente conductoras de sección S separadas una distancia a + b se encuentran dos capas de dieléctricos no ideales de espesores a y b respectivamente. Los dieléctricos tienen permitividades 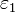 y
y 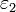 y conductividades σ1 y σ2, respectivamente. Entre las placas se aplica una diferencia de potencial constante mediante de una fuente de f.e.m.
y conductividades σ1 y σ2, respectivamente. Entre las placas se aplica una diferencia de potencial constante mediante de una fuente de f.e.m. 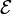 .
.
- Diseñe el circuito equivalente a este sistema.
- Calcule la corriente que atraviesa el dispositivo.
- Halle la carga en cada una de las placas y en la interfaz central entre los dos dieléctricos.
- Calcule la potencia disipada y la energía almacenada en el sistema.
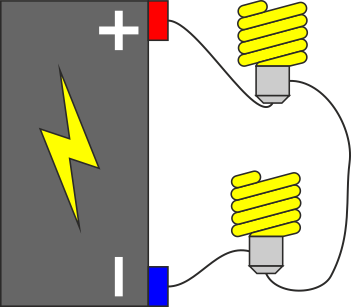
8 Conexiones de dos bombillas
Se desea encender dos bombillas de resistencia R0, para lo cual se dispone de una batería de f.e.m.  y resistencia interna r.
y resistencia interna r.
- En un primer montaje se disponen las dos bombillas en serie.
- Calcule la intensidad de corriente que circula por cada una.
- Halle la potencia que consumen (que dará una medida de la luz que desprenden).
- Calcule la potencia desarrollada por el generador y el consumo de energía en el propio generador.
- A continuación se prueba a montarlas en paralelo.
- Calcule la intensidad de corriente que circula por cada una.
- Halle la potencia que consumen.
- Calcule la potencia desarrollada por el generador y el consumo de energía en el propio generador.
- ¿En cuál de los dos montajes el conjunto de las dos bombillas dará más luz?
- Supongamos que tenemos una batería de 10 V y 1 Ω de resistencia interna y dos bombillas en cuya etiqueta pone “10V 25W”, ¿cómo deberemos montarlas para que den el máximo de luz? ¿Cuánta potencia consumirán en ese caso?

9 Conexiones de cuatro bombillas
Se dispone de cuatro bombillas, A, B, C, D. El etiquetado de estas bombillas indica que, para un voltaje de 120V, sus potencias nominales son respectivamente 30W, 60W, 120W y 40W. Se montas la cuatro bombillas en el siguiente esquema y se aplica entre los extremos una diferencia de potencial de 120V.
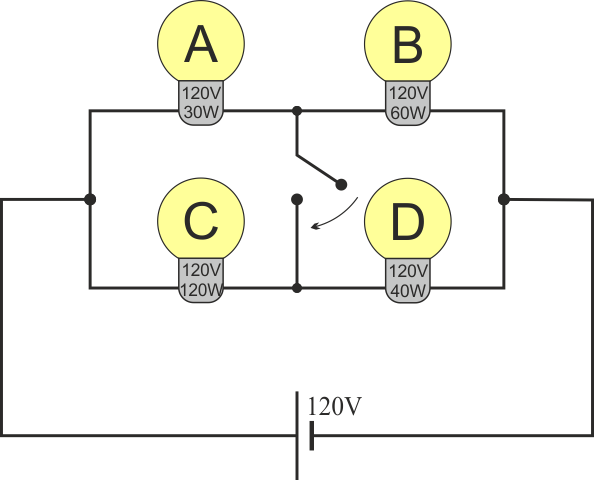
- Calcule el consumo de cada bombilla (en vatios) para este montaje, así como el consumo total del montaje. ¿Cuál es la que da más luz? ¿Y la que menos?
- Suponga que se cierra el interruptor central. Una vez cerrado, ¿cuál es el nuevo consumo total y el individual? ¿Cuál es ahora la bombilla más brillante y la menos brillante?





