Entrar Página Discusión Historial Go to the site toolbox

Problemas de dinámica vectorial (CMR2)

De Laplace

Contenido

1 Oscilador armónico tridimensional

Una partícula se mueve en tres dimensiones de forma tal que verifica la ecuación del oscilador armónico

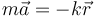
m\vec{a}=-k\vec{r}

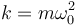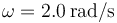con k=m\omega_0^2 y \omega = 2.0\,\mathrm{rad}/\mathrm{s}. Su posición inicial es \vec{r}_0=5\,\vec{\imath}\ (\mathrm{m}).

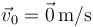  1. Para el caso \vec{v}_0=\vec{0}\,\mathrm{m}/\mathrm{s}. ¿Qué tipo de movimiento describe la partícula?
  2. Para el caso \vec{v}_0=10.0\,\vec{\jmath}\,\mathrm{m}/\mathrm{s}, ¿cómo es la trayectoria? ¿Qué tipo de movimiento describe la partícula?
  3. Suponga ahora que \vec{v}_0=8.0\,\vec{\jmath}\,\mathrm{m}/\mathrm{s}, ¿cómo es ahora la trayectoria de la partícula?
  4. Demuestre que en todos los casos la cantidad calculada en coordenadas polares 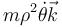m\rho^2\dot{\theta}\vec{k} es constante.

2 Dos masas unidas por un muelle

Dos masas m1 y m2 se mueven a lo largo del eje OX unidas por un resorte de constante k y longitud natura 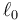\ell_0. Inicialmente las dos masas se encuentran en reposo en x10 = 0 y 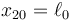x_{20}=\ell_0. Entonces se le comunica a la masa m1 una velocidad v0 en el sentido positivo del eje.

  1. Determine dos constantes de movimiento.
  2. Calcule la posición de cada una de las masas como función del tiempo. Sugerencia: realice el cambio de variables xG = (m1x1 + m2x2) / (m1 + m2), x=x_2-x_1-\ell_0.

3 Dos masas unidas por un oscilador armónico

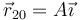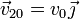Suponga que en el problema “Oscilador armónico tridimensional” en lugar de una sola partícula tenemos dos, de masas m1 y m2, unidas por un resorte de constante k y longitud natural nula. Inicialmente la masa 1 se halla en reposo en el origen de coordenadas y la masa 2 se encuentra en \vec{r}_{20}=A\vec{\imath} moviéndose con velocidad \vec{v}_{20}=v_0\vec{\jmath}.

  1. Demuestre que el centro de masas de las dos partículas describe un movimiento rectilíneo y uniforme.
  2. Considerando la posición de cada partícula respecto al CM, determine la posición de cada una de ellas como función del tiempo.

4 Movimiento a partir de una fuerza conocida

Una partícula material de masa m parte del origen de coordenadas con velocidad 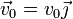\vec{v}_0=v_0\vec{\jmath}, encontrándose sometida en todo momento a la fuerza dependiente de la posición

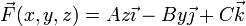
\vec{F}(x,y,z)=Az\vec{\imath}-By\vec{\jmath}+C\vec{k}

siendo 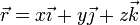\vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k} la posición instantánea de la partícula, y A, B y C constantes positivas conocidas.

Calcule la posición, velocidad y aceleración instantáneas de la partícula para todo instante de tiempo, t.

5 Doble máquina de Atwood

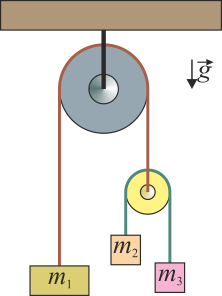
La doble máquina de Atwood de la figura está formada por tres masas unidas a través de dos cuerdas ideales (inextensibles y sin masa) y dos poleas también ideales (de masa despreciable y sin rozamiento). Determine la aceleración de cada una de las masas, así como las tensiones de las dos cuerdas.

Archivo:doble-maquina-atwood.png

6 Péndulo en caja deslizante

Una caja cúbica de gran masa desciende sin rozamiento por un plano inclinado un ángulo β. En el interior de la caja se encuentra un péndulo (de masa mucho menor que la de la caja) que cuelga de su techo.

  1. Si el péndulo no oscila, determine el ángulo θ que forma el péndulo con la vertical.
  2. Suponga ahora que entre la caja y el plano hay una fricción dinámica de coeficiente μ. Determine el ángulo de inclinación en ese caso.
  3. Para los dos casos anteriores, supóngase que el péndulo se separa ligeramente de su posición de equilibrio, ¿cuál será la frecuencia de las oscilaciones que experimenta?

7 Anilla ensartada en un aro

Se tiene un aro circular de radio R situado verticalmente. Determine la velocidad que debe comunicarse a una partícula de masa m situada en el punto más bajo del aro para que sea capaz de llegar hasta el punto más alto si la partícula es:

  • Una anilla ensartada en el aro
  • Una bolita que desliza por el interior del aro, sin estar unida a él.
  1. Calcule la reacción que ejerce el aro sobre la partícula en el punto más bajo y en el más alto, para los dos casos anteriores. Desprecie el rozamiento en todos los casos.
  2. Para el caso (b), suponga que a la partícula se le comunica la velocidad inicial calculada en (a), ¿en qué punto se desprende del aro?

8 Partícula que sale despedida de una semiesfera

Una partícula de masa m se encuentra en lo alto de una cúpula hemisférica de radio R, sobre la cual la masa puede deslizar sin rozamiento. La semiesfera está rígidamente unida a una superficie horizontal. La masa está sometida a la acción del peso. Estando en esta posición se le comunica una velocidad horizontal de rapidez v0

Supóngase en primer lugar que v_0=0.

  1. Determine el punto en el que la masa despega de la superficie esférica, dando el ángulo θ que el vector de posición relativa al centro de la esfera forma con la vertical.
  2. ¿Qué rapidez tiene la partícula en el momento en que impacta con el suelo?

Supongamos ahora una cierta rapidez inicial v0.

  1. Determine el punto en el que la masa despega de la superficie esférica, dando el ángulo θ que el vector de posición relativa al centro de la esfera forma con la vertical.
  2. ¿Cuál es el valor mínimo de v0 para que la partícula despegue directamente de la superficie, sin deslizar sobre ella?
  3. Para este valor mínimo de v0 determine la distancia al centro de la semiesfera del punto de la superficie horizontal en el que impacta la partícula.

9 Partícula cargada en campo magnético uniforme

Una carga q en campo magnético experimenta una fuerza

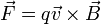
\vec{F}=q\vec{v}\times\vec{B}

Se trata de deducir cómo se mueve la partícula en el caso en el que el campo magnético sea una constante independiente de la posición.

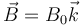
\vec{B}=B_0\vec{k}
  1. Suponga en primer lugar que la velocidad inicial de la partícula es paralela al campo magnético, 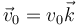\vec{v}_0 = v_0\vec{k}. ¿Cuánto vale la aceleración en el instante inicial? ¿Cuanto vale la velocidad un instante posterior? ¿Cómo es el movimiento de la carga en ese caso?
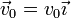  2. Suponga ahora el caso de una carga cuya velocidad inicial es perpendicular al campo magnético, \vec{v}_0 = v_0\vec{\imath}.
    1. Demuestre que el movimiento resultante es un movimiento plano.
    2. Demuestre que la rapidez del movimiento es constante
    3. Calcule el radio de curvatura de la trayectoria que describe la carga
    4. ¿Qué tipo de movimiento describe la partícula?
  3. Suponga, por último, una velocidad inicial arbitraria 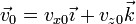\vec{v}_0 = v_{x0}\vec{\imath}+v_{z0}\vec{k}. Combinando los resultados anteriores, ¿qué movimiento realiza la carga?

10 Dos masas en planos inclinados y un muelle

Dos masas iguales de peso 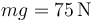mg=75\,\mathrm{N} situadas sobre dos planos inclinados contiguos, de las dimensiones mostradas en la figura. Las dimensiones son tales que el ángulo en O es recto.

Las masas están unidas por un resorte ideal de longitud natural nula y constante 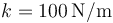k=100\,\mathrm{N}/\mathrm{m}. No hay rozamiento con las superficies.

  1. Determine la posición de equilibrio de las dos masas, hallando los valores de x e y.
  2. Para esta posición de equilibrio, calcule las fuerzas de reacción ejercidas por los planos, así como la fuerza elástica que el resorte ejerce sobre cada masa.
  3. Suponga ahora que existe un coeficiente de rozamiento estático μ = 0.25 entre las masas y las superficies en que se apoyan. En ese caso hay un rango de posiciones en las que puede producirse el equilibrio. ¿Cuánto valen x e y para la posición de equilibrio con mínima longitud del resorte? ¿Y para el caso de máxima longitud del resorte?
  4. Volviendo al caso sin rozamiento, determine las ecuaciones de movimiento para las dos masas.

Sugerencia: Empléense los ejes de la figura.

11 Fuerza en anilla ensartada en varillas

Para el sistema de la anilla ensartada en dos varillas, calcule la fuerza que cada una de las barras ejerce cada instante sobre la anilla, suponiendo ésta de masa m, (a) despreciando el peso, (b) considerando el peso en la dirección de OY negativo. Tenga en cuenta que cada barra solo puede ejercer fuerza perpendicularmente a sí misma, no a lo largo de ella.

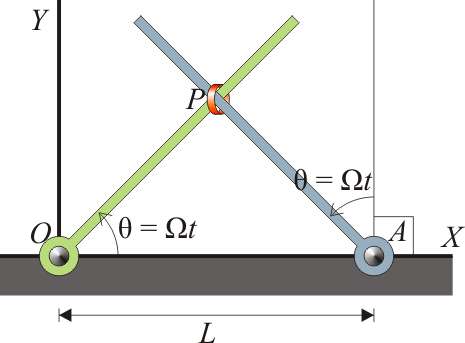
Archivo:anilla-dos-varillas.png

12 Partícula en el interior de un tubo

Una partícula de masa m se encuentra en el interior de un tubo estrecho, el cual se halla en todo momento contenido en el plano OXY girando con velocidad angular ω constante alrededor del eje OZ, de forma que la posición de la partícula puede escribirse como

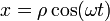
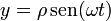
x = \rho\,\mathrm{cos}(\omega t)\,        y= \rho\,\mathrm{sen}(\omega t)

donde 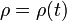\rho = \rho(t)\,, función que hay que determinar, define la posición de la partícula a lo largo del tubo.

  1. Halle la ecuación diferencial que debe satisfacer 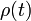\rho(t)\, sabiendo que el tubo no puede ejercer fuerza en la dirección longitudinal (no hay rozamiento).
  2. Calcule la solución de esta ecuación de movimiento si la partícula se encuentra inicialmente a una distancia A del eje de giro con velocidad radial nula.
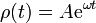
  3. Suponga que \rho(t) =A\mathrm{e}^{\omega t}\,
  4. Calcule la fuerza ejercida por el tubo en cada instante para una posición y velocidades arbitrarias y para la solución anterior.
  5. Si se analiza este movimiento desde un sistema de referencia ligado al tubo
    1. ¿Qué fuerzas actúan sobre la partícula?
    2. ¿Cuál de ellas acelera a la partícula? ¿Por qué aparece una fuerza del tubo sobre la partícula?

13 Partícula en un cuenco esférico

Una partícula de masa m puede deslizarse sin fricción por la superficie de un cuenco esférico fijo de ecuación x^2+y^2+z^2=b^2 sometida a la acción del peso (en la dirección y sentido de z decreciente) y de la fuerza de reacción vincular.

  1. Para cada altura h respecto al fondo la partícula puede describir un movimiento circular horizontal si tiene la rapidez adecuada.
    1. ¿Cuál sería esta rapidez?
    2. ¿Y el periodo de revolución?
    3. ¿Cuánto vale la fuerza de reacción vincular en este movimiento?
  2. Escriba las ecuaciones de movimiento para una situación arbitraria de la masa sobre la superficie esférica, empleando como variables:
    1. Las coordenadas cartesianas
    2. Las coordenadas esféricas centradas en el centro de la esfera,
  3. Suponga que la partícula se ve restringida a moverse en el plano y = 0 y que se desplaza en el eje OX una ligera cantidad (x_0\ll b). ¿Cuál es la frecuencia de las oscilaciones que describe?
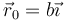    1. Si la partícula se suelta desde el reposo en \vec{r}_0=b\vec{\imath}, ¿qué velocidad lleva cuando pasa por el fondo del pozo? ¿Cuánto vale la fuerza de reacción vincular en ese punto? ¿Cuánto vale a mitad de camino?

14 Partícula en paraboloide

Suponga un problema similar al de la partícula en un cuenco esférico pero con la partícula sobre un paraboloide de ecuación z = (x2 + y2) / (2b)

  1. Para cada altura h respecto al fondo la partícula puede describir un movimiento circular horizontal si tiene la rapidez adecuada. ¿Cuál sería esta rapidez? ¿Y el periodo de revolución? ¿Cuánto vale la fuerza de reacción vincular en este movimiento?
  2. Escriba las ecuaciones de movimiento para una situación arbitraria de la masa sobre el paraboloide, empleando como variables:
    1. Las coordenadas cartesianas
    2. Las coordenadas cilíndricas, eliminando las fuerzas de reacción vincular.
  3. Suponga que la partícula se ve restringida a moverse en el plano y=0 y que se desplaza en el eje OX una ligera cantidad (x_0\ll b). ¿Cuál es la frecuencia de las oscilaciones que describe?
  4. Si la partícula se suelta desde el reposo en 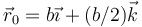\vec{r}_0=b\vec{\imath}+(b/2)\vec{k}, ¿qué velocidad lleva cuando pasa por el fondo del pozo? ¿Cuánto vale la fuerza de reacción vincular en ese punto? ¿Cuánto vale a mitad de camino?
Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_din%C3%A1mica_vectorial_(CMR2)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace