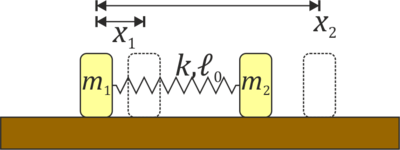
Dos masas unidas por un muelle

De Laplace

Contenido

1 Enunciado
2 Ecuaciones de movimiento
3 Constantes de movimiento
- 3.1 Cantidad de movimiento del sistema
- 3.2 Energía mecánica
4 Ecuaciones horarias

1 Enunciado

Dos masas $m 1$ y $m 2$ se mueven a lo largo del eje OX unidas por un resorte de constante $k$ y longitud natura 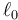$\ell_0$ . Inicialmente las dos masas se encuentran en reposo en $x 10 = 0$ y 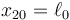$x_{20}=\ell_0$ . Entonces se le comunica a la masa $m 1$ una velocidad $v 0$ en el sentido positivo del eje.

Determine dos constantes de movimiento.
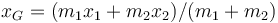Calcule la posición de cada una de las masas como función del tiempo. Sugerencia: realice el cambio de variables $x_G=(m_1 x_1+m_2 x_2)/(m_1+m_2)\,$ , $x=x_2-x_1-\ell_0$ .

2 Ecuaciones de movimiento

Las dos masas describen un movimiento rectilíneo, por lo que podemos emplear cantidades escalares, en lugar de vectores.

En ese caso, la segunda ley de Newton aplicada a cada partícula nos da

$m_1\ddot{x}_1 = F_1\qquad\qquad m_2\ddot{x}_2 = F_2$

La fuerza que actúa sobre cada partícula es la debida al resorte (aparte estarían el peso y la normal, pero se cancelan mutuamente, por lo que no influyen). Esta fuerza está gobernada por la ley de Hooke

$F_1= k(x_2-x_1-\ell_0)\qquad\qquad F_2=-k(x_2-x_1-\ell_0)$

donde el signo es tal que si el muelle está estirado tiende a reunir las dos masas.

Por tanto, tenemos el sistema de ecuaciones diferenciales

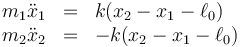
$\begin{array}{rcl} m_1 \ddot{x}_1 & = & k(x_2-x_1-\ell_0) \\ m_2 \ddot{x}_2 & = & -k(x_2-x_1-\ell_0) \end{array}$

con las condiciones iniciales, en este caso

$x_{10}=0\qquad\qquad\dot{x}_{10}=v_0\qquad\qquad x_{20}=\ell_0\qquad\qquad\dot{x}_{20}=0$

3 Constantes de movimiento

De las ecuaciones de movimiento se deducen dos integrales primeras o constantes de movimiento:

3.1 Cantidad de movimiento del sistema

Sumando las dos ecuaciones

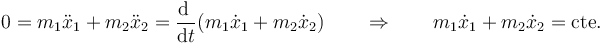
$0=m_1\ddot{x}_1+m_2\ddot{x}_2=\frac{\mathrm{d}\ }{\mathrm{d}t}(m_1\dot{x}_1+m_2\dot{x}_2)\qquad\Rightarrow\qquad m_1\dot{x}_1+m_2\dot{x}_2=\mathrm{cte}.$

con las condiciones iniciales de este problema

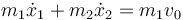
$m_1\dot{x}_1+m_2\dot{x}_2=m_1v_0$

Esta ecuación puede ser integrada de nuevo

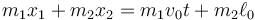
$m_1x_1+m_2x_2=m_1v_0 t + m_2\ell_0$

De la conservación de la cantidad de movimiento se halla la velocidad y posición del CM

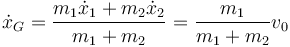
$\dot{x}_G=\frac{m_1\dot{x}_1+m_2\dot{x}_2}{m_1+m_2}= \frac{m_1}{m_1+m_2}v_0$

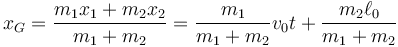
$x_G=\frac{m_1x_1+m_2x_2}{m_1+m_2}= \frac{m_1}{m_1+m_2}v_0t+\frac{m_2\ell_0}{m_1+m_2}$

Vemos que el CM se mueve uniformemente, aunque su velocidad no es $v 0$ sino una cantidad inferior.

3.2 Energía mecánica

Este sistema es conservativo, siendo su energía potencial

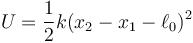
$U=\frac{1}{2}k(x_2-x_1-\ell_0)^2$

Por tanto se conserva su energía mecánica

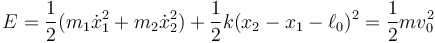
$E = \frac{1}{2}(m_1\dot{x}_1^2+m_2\dot{x}_2^2)+\frac{1}{2}k(x_2-x_1-\ell_0)^2= \frac{1}{2}mv_0^2$

4 Ecuaciones horarias

Para resolver el sistema de ecuaciones de movimiento

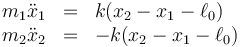
$\begin{array}{rcl} m_1 \ddot{x}_1 & = & k(x_2-x_1-\ell_0) \\ m_2 \ddot{x}_2 & = & -k(x_2-x_1-\ell_0) \end{array}$

realizamos un cambio de variables. En lugar de las posiciones respectivas tomaremos la posición del CM

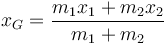
$x_G=\frac{m_1x_1+m_2x_2}{m_1+m_2}$

y la elongación del resorte

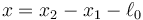
$x = x_2-x_1-\ell_0\,$

Una vez que determinemos estas dos cantidades como función del tiempo, podemos hallar la posición de cada masa invirtiendo estas relaciones

$x_1= x_G-\frac{m_2}{m_1+m_2}(x+\ell_0)\qquad\qquad x_2=x_G+\frac{m_1}{m_1+m_2}(x+\ell_0)$

La posición del CM como función del tiempo ya la hemos determinado a partir de la conservación de la cantidad de movimiento

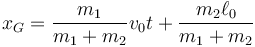
$x_G=\frac{m_1}{m_1+m_2}v_0t+\frac{m_2\ell_0}{m_1+m_2}$

Nos queda hallar la ecuación para la elongación y resolverla. Las ecuaciones de movimiento las podemos escribir en la forma

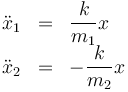
$\begin{array}{rcl} \ddot{x}_1 & = & \dfrac{k}{m_1}x \\ \ddot{x}_2 & = & -\dfrac{k}{m_2}x \end{array}$

Si restamos la primera de la segunda obtenemos la segunda derivada de la elongación

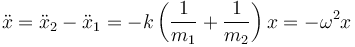
$\ddot{x}=\ddot{x}_2-\ddot{x}_1=-k\left(\frac{1}{m_1}+\frac{1}{m_2}\right)x = -\omega^2 x$

que es la ecuación del oscilador armónico con la frecuencia al cuadrado

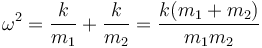
$\omega^2 = \frac{k}{m_1}+\frac{k}{m_2}=\frac{k(m_1+m_2)}{m_1m_2}$

La solución de esta ecuación diferencial es de la forma

$x=c_1 \cos(\omega t)+c_2\,\mathrm{sen}(\omega t)$

con los coeficientes que salen de las condiciones iniciales. En este caso tenemos

$x(t=0)=x_{20}-x_{10}-\ell_0=0\qquad\qquad \dot{x}(t=0)=\dot{x}_{20}-\dot{x}_{10}=-v_0$

Llevamos esto a la expresión de $x (t)$

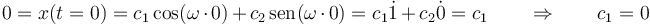
$0=x(t=0)=c_1 \cos(\omega\cdot 0)+c_2\,\mathrm{sen}(\omega\cdot 0)=c_1\dot 1 + c_2\dot 0 = c_1\qquad\Rightarrow\qquad c_1=0$

y de 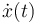$\dot{x}(t)$

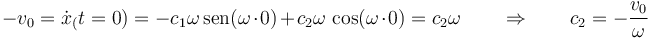
$-v_0=\dot{x}_(t=0)=-c_1\omega\,\mathrm{sen}(\omega\cdot 0) + c_2\omega\,\cos(\omega\cdot 0)=c_2\omega\qquad\Rightarrow\qquad c_2=-\frac{v_0}{\omega}$

Por tanto la elongación como función del tiempo es de la forma

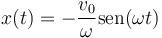
$x(t)=-\frac{v_0}{\omega}\mathrm{sen}(\omega t)$

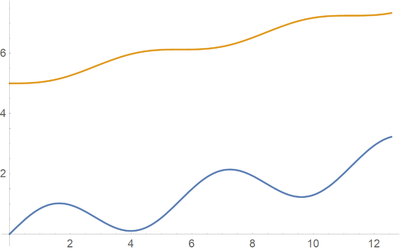
A partir de aquí obtenemos la posición de cada masa como función del tiempo

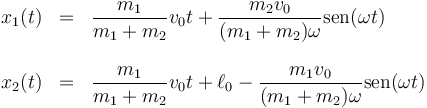
$\begin{array}{rcl} x_1(t)&=&\dfrac{m_1}{m_1+m_2}v_0t+\dfrac{m_2v_0}{(m_1+m_2)\omega}\mathrm{sen}(\omega t)\\ && \\ x_2(t) & = & \dfrac{m_1}{m_1+m_2}v_0t+\ell_0-\dfrac{m_1v_0}{(m_1+m_2)\omega}\mathrm{sen}(\omega t) \end{array}$

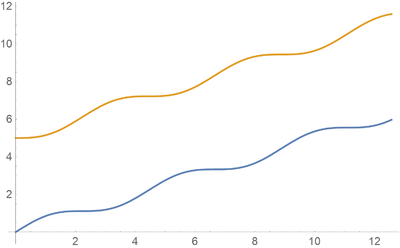
En las gráficas podemos ver el resultado para el caso de que la masa 1 sea igual a la 2, el que la 1 sea más masiva (y por tanto apenas se ve afectada por el resorte) o que sea muy ligera (en cuyo caso rebota y retrocede periódicamente).

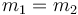
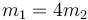
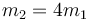
$m_1=m_2\,$	$m_1=4m_2\,$	$m_2=4m_1\,$

En términos de las cantidades $x G$ y $x$ las dos constantes de movimiento se escriben

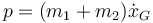
$p=(m_1+m_2)\dot{x}_G$

y

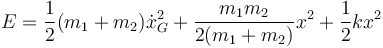
$E=\frac{1}{2}(m_1+m_2)\dot{x}_G^2+\frac{m_1m_2}{2(m_1+m_2)}x^2+\frac{1}{2}kx^2$

De estos tres términos, el primero es constante y representa la energía por moverse con el centro de masas y los otros dos suman la energía de un oscilador armónico, representando el movimiento alrededor del CM.

Dos masas unidas por un muelle

De Laplace

Contenido

1 Enunciado

2 Ecuaciones de movimiento

3 Constantes de movimiento

3.1 Cantidad de movimiento del sistema

3.2 Energía mecánica

4 Ecuaciones horarias

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES