Anilla ensartada en un aro (CMR)
De Laplace
Contenido |
1 Enunciado
Se tiene un aro circular de radio R situado verticalmente. Determine la velocidad que debe comunicarse a una partícula de masa m situada en el punto más bajo del aro para que sea capaz de llegar hasta el punto más alto si la partícula es:
- Una anilla ensartada en el aro.
- Una bolita que desliza por el interior del aro, sin estar unida a él.
- Calcule la reacción que ejerce el aro sobre la partícula en el punto más bajo y en el más alto, para los dos casos anteriores. Desprecie el rozamiento en todos los casos.
- Para el segundo caso, suponga que a la partícula se le comunica la velocidad inicial calculada en el primero, ¿en qué punto se desprende del aro?
2 Planteamiento
Podemos analizar todos los casos simultáneamente, particularizando posteriormente a los casos indicados.
2.1 Posición, velocidad y aceleración
La particula se encuentra obligada a a moverse sobre una circunferencia, por lo que podemos parametrizar su posición como
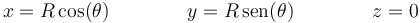
siendo θ el ángulo con la vertical hacia abajo, que es nuestro eje X. El Y es el horizontal y el Z el perpendicular al plano de movimiento. De esta manera el paso de cartesianas a polares es inmediato.
Usando las abreviaturas que emplearemos en lo sucesivo:

queda
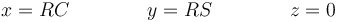
La velocidad de esta partícula, expresada en la base cartesiana es
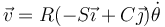
y, en la de polares,
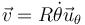
La aceleración, en polares, queda
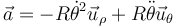
2.2 Fuerzas
La partícula se mueve sometida a la acción del peso
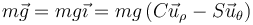
y de la reacción del aro
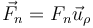
aquí no estamos suponiendo que la fuerza vaya en el sentido hacia el exterior, solo que va en la dirección radial. Fn puede ser una cantidad negativa.
Llevando esto a la segunda ley de Newton queda, para la componente radial
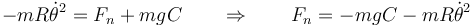
y para la acimutal

Esta es la ecuación de un péndulo simple, al cual este sistema es equivalente.
La primera ecuación nos permite hallar la fuerza de reacción. La podemos expresar en función de la rapidez en cada punto
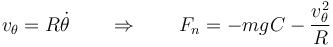
2.3 Energía mecánica
De las dos fuerzas que actúan sobre la partícula, la reacción normal es perpendicular en todo momento a la velocidad, por lo que no realiza trabajo. El peso sí, pero es una fuerza conservativa. Por tanto, se conserva la energía mecánica de la partícula. Igualando la que tiene en cada momento a la inicial queda la relación
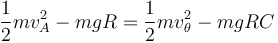
de la cual podemos despejar la rapidez inicial, vA o la que tiene en cada punto.
3 Caso de la anilla
En el caso de una anilla ensartada en el aro tenemos una partícula que se ve obligada a moverse a lo largo de la circunferencia en todo momento. Esto constituye un ejemplo de un vínculo bilateral ya que la partícula no puede separarse de la circunferencia ni en un sentido ni en otro. Por tanto, la fuerza de reacción puede ir tanto hacia adentro (e impide que la anilla se salga), como hacia afuera (e impide que caiga hacia adentro)
La velocidad mínima es aquella que hace llegar a la anilla al punto más alto con velocidad nula. La conservación de la energía nos da
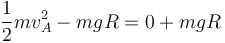
con lo que la velocidad mínima es
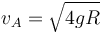
En el punto más alto, la fuerza activa aplicada, el peso, es puramente normal a la trayectoria. La única aceleración de la partícula será normal, pero al llegar con velocidad nula, la aceleración normal vale cero. Por tanto se cumple
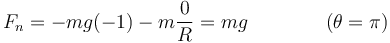
por tanto, la fuerza de reacción vincular compensa exactamente al peso. Esta fuerza tiene signo positivo, lo que indica que va en la dirección radial hacia afuera.
En el punto más bajo, tanto el peso como la reacción son normales al aro
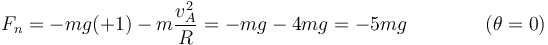
esto es, con la anilla en movimiento, el aro debe ejercer una fuerza igual a cinco veces el peso. El signo negativo indica que va en la dirección radial hacia adentro.
4 Bola
En el segundo caso tenemos una bola que se mueve en contacto con el aro, por el interior de éste, pero sin estar unida a él. Tenemos ahora un vínculo unilateral, ya que el aro puede impedir que el radio de la trayectoria supere el valor de R, pero no puede evitar que sea menor, esto es, que la partícula puede caerse al llegar a una cierta altura, ya que no hay nada que la retenga.
Matemáticamente, esto se manifiesta en que la fuerza de reacción vincular no puede tener los dos sentidos normales, sino solo uno de ellos. Siempre debe ir dirigida hacia adentro, nunca hacia afuera.

Esto implica que el resultado del apartado anterior no es aplicable a este caso, ya que la reacción vincular en el punto más alto no podría ir dirigida hacia arriba para retener la bolita. Lo que ocurriría al comunicarle esa velocidad es que llegado a una cierta altura, la bolita se separaría del aro y caería describiendo una parábola.
Si queremos que la partícula llegue hasta arriba debemos comunicarle una velocidad tal que la fuerza de reacción vincular se dirija hacia arriba, siendo el valor mínimo de la velocidad aquél que produce una reacción vincular nula.
Puesto que ahora la partícula llega con velocidad distinta de cero, la partícula posee una aceleración normal en el punto más alto, por lo que debe cumplirse
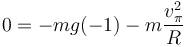
de donde la velocidad en el punto más alto cumple
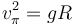
La velocidad en el punto inferior la obtenemos aplicando de nuevo la ley de conservación de la energía mecánica
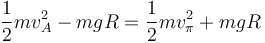
lo que nos da la nueva velocidad inicial
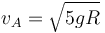
La reacción vincular en el punto más alto es nula, según hemos indicado
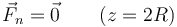
En el punto más bajo, de nuevo el peso y la reacción son normales al aro por lo que
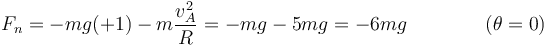
Ahora el aro debe ejercer una fuerza igual a seis veces el peso.
5 Desprendimiento
Si a la masa se le da una velocidad inicial inferior a la necesaria, llega un punto en el que se desprende del aro, incluso aunque su velocidad en ese momento sea distinta de cero. Esto ocurre cuando se anula la fuerza de reacción normal.
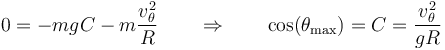
El signo menos indica que el desprendimiento siempre ocurre en la mitad superior del aro (π/2 < θ < π).
Podemos relacionar este resultado con la velocidad inicial a partir de la conservación de la energía mecánica
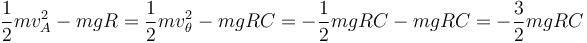
lo que nos da el ángulo de desprendimiento
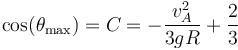
Vemos que si 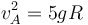 resulta un coseno igual a −1, lo que indica que llega hasta arriba.
resulta un coseno igual a −1, lo que indica que llega hasta arriba.
Si 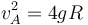 no llega hasta arriba. Se separa en
no llega hasta arriba. Se separa en
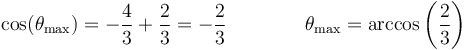
La altura a la que esto ocurre, respecto al punto más bajo del aro, es en
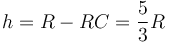
6 Movimiento posterior
En el momento de la separación, la partícula se encuentra en
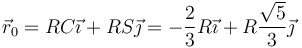
moviéndose con velocidad
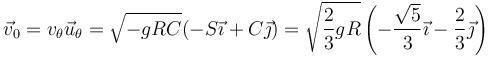
Su movimiento posterior es parabólico
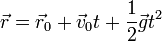
siendo la componente x
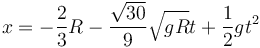
y la y
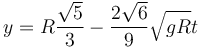
La partícula vuelve a impactar con el aro cuando
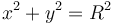
La analogía con un péndulo consiste en suponer uno con un hilo flexible. Cuando su tensión se hace cero el hilo se destensa y la masa pasa a describir un movimiento parabólico hasta que el hilo vuelve a tensarse.





