Dos masas en planos inclinados y un muelle

De Laplace

Contenido

1 Enunciado
2 Posición de equilibrio
3 Fuerzas de reacción
4 Caso con rozamiento
- 4.1 Mínima longitud del resorte
- 4.2 Máxima longitud del resorte

1 Enunciado

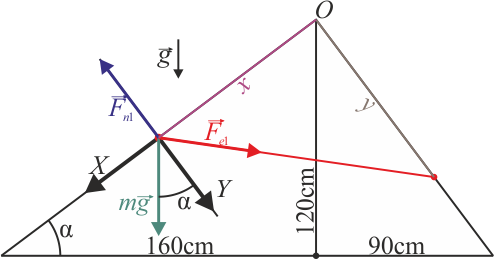
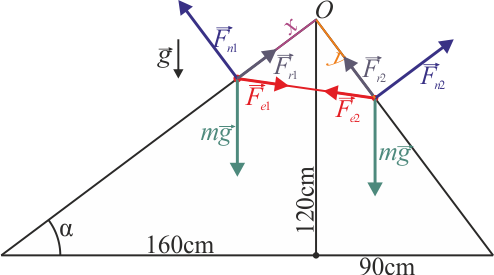
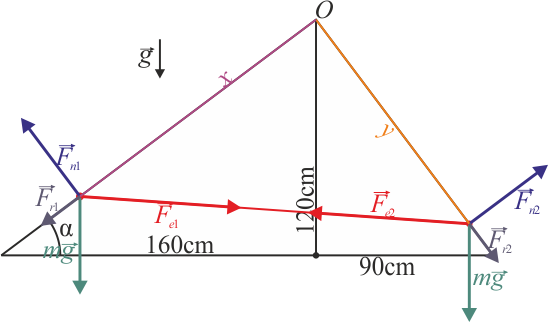
Dos masas iguales de peso 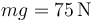$mg=75\,\mathrm{N}$ situadas sobre dos planos inclinados contiguos, de las dimensiones mostradas en la figura. Las dimensiones son tales que el ángulo en O es recto.

Las masas están unidas por un resorte ideal de longitud natural nula y constante 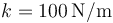$k=100\,\mathrm{N}/\mathrm{m}$ . No hay rozamiento con las superficies.

Determine la posición de equilibrio de las dos masas, hallando los valores de $x$ e $y$ .
Para esta posición de equilibrio, calcule las fuerzas de reacción ejercidas por los planos, así como la fuerza elástica que el resorte ejerce sobre cada masa.
Suponga ahora que existe un coeficiente de rozamiento estático μ = 0.25 entre las masas y las superficies en que se apoyan. En ese caso hay un rango de posiciones en las que puede producirse el equilibrio. ¿Cuánto valen $x$ e $y$ para la posición de equilibrio con mínima longitud del resorte? ¿Y para el caso de máxima longitud del resorte?

Sugerencia: Empléense los ejes de la figura.

2 Posición de equilibrio

Por estar en equilibrio, la suma de las fuerzas sobre cada masa debe anularse.

Si llamamos masa “1” a la de la izquierda tenemos que las fuerzas que actúan sobre ella son:

Peso: que en los ejes indicados valen

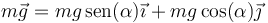
$m\vec{g}=mg\,\mathrm{sen}(\alpha)\vec{\imath}+mg\cos(\alpha)\vec{\jmath}$

con

$\mathrm{tg}(\alpha)=\frac{120}{160}=\frac{3}{4}\qquad\Rightarrow\qquad \mathrm{sen}(\alpha)=\frac{3}{5}\qquad\cos(\alpha)=\frac{4}{5}$

lo que da el valor numérico

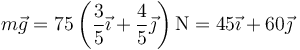
$m\vec{g}=75\left(\frac{3}{5}\vec{\imath}+\frac{4}{5}\vec{\jmath}\right)\mathrm{N}=45\vec{\imath}+60\vec{\jmath}$

Fuerza elástica: Cuando la longitud natural de un resorte es nula, la fuerza elástica que produce la da la ley de Hooke vectorial es proporcional al vector de posición relativa. Si queremos hallar la fuerza en el extremo A, hallándose el otro extremo en el punto B

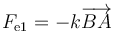
$F_\mathrm{e1}=-k\overrightarrow{BA}$

siendo 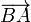$\overrightarrow{BA}$ el vector que va desde el extremo B del muelle hasta el A, que ocupa la partícula 1. En este caso sería

$\overrightarrow{OA}=x\vec{\imath}\qquad\qquad \overrightarrow{OB}=y\vec{\jmath}$

Restando

$\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}=x\vec{\imath}-y\vec{\jmath}$

y por tanto

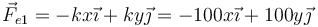
$\vec{F}_{e1}=-kx\vec{\imath}+ky\vec{\jmath}=-100x\vec{\imath}+100y\vec{\jmath}$

Reacción normal del plano: Esta es perpendicular al plano y va en el sentido hacia afuera

$\vec{F}_{n1}=-F_{n1}\vec{\jmath}$

Archivo:dos-planos-inclinados-muelle-02.png

Sumando las tres fuerzas

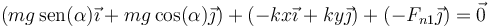
$\left(mg\,\mathrm{sen}(\alpha)\vec{\imath}+mg\cos(\alpha)\vec{\jmath}\right)+\left(-kx\vec{\imath}+ky\vec{\jmath}\right)+\left(-F_{n1}\vec{\jmath}\right)=\vec{0}$

y separando en componentes

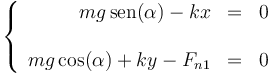
$\left\{\begin{array}{rcl} mg\,\mathrm{sen}(\alpha) - kx & = & 0 \\ && \\ mg\cos(\alpha) + ky - F_{n1} & = & 0 \end{array}\right.$

De aquí obtenemos de forma inmediata el valor de $x$ en el equilibrio

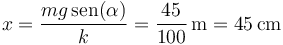
$x = \frac{mg\,\mathrm{sen}(\alpha)}{k}=\frac{45}{100}\,\mathrm{m}=45\,\mathrm{cm}$

Para obtener el valor de y hacemos el cálculo análogo para la segunda masa. Para esta

Peso: Al igual que antes

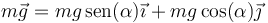
$m\vec{g}=mg\,\mathrm{sen}(\alpha)\vec{\imath}+mg\cos(\alpha)\vec{\jmath}$

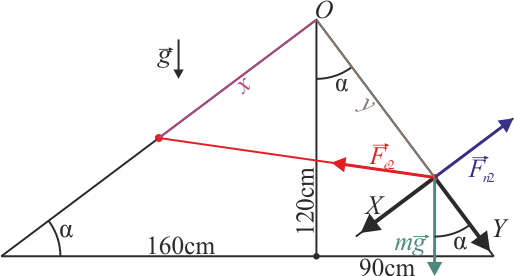
Fuerza elástica: Aplicando el mismo razonamiento para esta masa o simplemente por la tercera ley de Newton

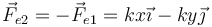
$\vec{F}_{e2}=-\vec{F}_{e1}=kx\vec{\imath}-ky\vec{\jmath}$

Reacción normal del plano: Esta es perpendicular al segundo plano

$\vec{F}_{n2}=-F_{n2}\vec{\imath}$

Archivo:dos-planos-inclinados-muelle-03.png

Sumando estas tres fuerzas

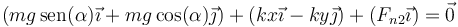
$\left(mg\,\mathrm{sen}(\alpha)\vec{\imath}+mg\cos(\alpha)\vec{\jmath}\right)+\left(kx\vec{\imath}-ky\vec{\jmath}\right)+\left(F_{n2}\vec{\imath}\right)=\vec{0}$

que separando en componentes da

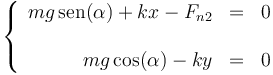
$\left\{\begin{array}{rcl} mg\,\mathrm{sen}(\alpha) + kx -F_{n2} & = & 0 \\ && \\ mg\cos(\alpha) - ky & = & 0 \end{array}\right.$

que nos da el valor de $y$ en el equilibrio

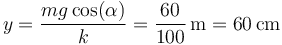
$y = \frac{mg\,\mathrm{cos}(\alpha)}{k}=\frac{60}{100}\,\mathrm{m}=60\,\mathrm{cm}$

siendo la longitud del muelle

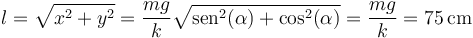
$l= \sqrt{x^2+y^2}=\frac{mg}{k}\sqrt{\mathrm{sen}^2(\alpha)+\cos^2(\alpha)}=\frac{mg}{k}=75\,\mathrm{cm}$

3 Fuerzas de reacción

Una vez que tenemos x e y obtenemos las fuerzas normales

$F_{n1}=mg\,\mathrm{sen}(\alpha)+ky=2mg\,\mathrm{sen}(\alpha)=90\,\mathrm{N}$

y

$F_{n2}=mg\,\mathrm{cos}(\alpha)+kx=2mg\,\mathrm{cosn}(\alpha)=120\,\mathrm{N}$

En forma vectorial

$\vec{F}_{n1}=-2mg\,\mathrm{sen}(\alpha)\vec{\jmath}=-90\vec{\jmath}\,\mathrm{N}\qquad\qquad \vec{F}_{n2}=-2mg\,\mathrm{cos}(\alpha)\vec{\jmath}=-120\vec{\jmath}\,\mathrm{N}$

Cuando la figura se realiza correctamente a escala vemos que efectivamente el resorte no queda en una posición horizontal y que para cada masa, la suma vectorial de las tres fuerzas aplicadas es nula.

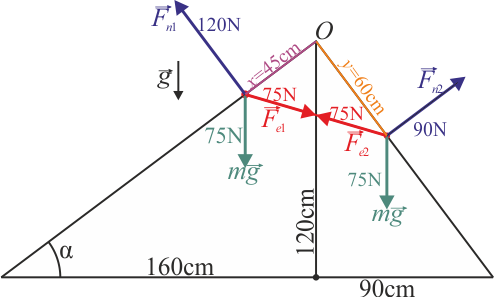
Archivo:dos-planos-inclinados-muelle-06.png

4 Caso con rozamiento

Cuando hay rozamiento hay que añadir fuerzas tangenciales de rozamiento, con lo que la ecuación para la partícula 1 se convierte en

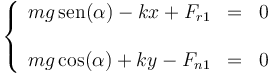
$\left\{\begin{array}{rcl} mg\,\mathrm{sen}(\alpha) - kx +F_{r1}& = & 0 \\ && \\ mg\cos(\alpha) + ky - F_{n1} & = & 0 \end{array}\right.$

y para la 2

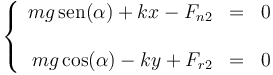
$\left\{\begin{array}{rcl} mg\,\mathrm{sen}(\alpha) + kx -F_{n2} & = & 0 \\ && \\ mg\cos(\alpha) - ky +F_{r2} & = & 0 \end{array}\right.$

El valor de la fuerza de rozamiento depende de la posición de la masa, ya que en el equilibrio, lo más que podemos asegurar es que

$|\vec{F}_{ri}|\leq \mu |\vec{F}_{ni}|\qquad \qquad i = 1,2$

4.1 Mínima longitud del resorte

Cuando la longitud del muelle se reduce respecto a la calculada anteriormente, las masas se hallan en un punto superior del plano. En este punto, la fuerza elástica es menor (porque el muelle está menos estirado), por lo que no es capaz de igualar al peso. Las masas tienden a irse hacia abajo. Si no lo hacen es porque hay una fuerza de rozamiento hacia arriba (en contra del posible movimiento).

Archivo:dos-planos-inclinados-muelle-04.png

En el caso de la longitud mínima, la fuerza de rozamiento alcanza su mayor valor posible, por tanto

$\vec{F}_{r1}=-\mu F_{n1}\vec{\imath}\qquad\qquad \vec{F}_{r2}=-\mu F_{n2}\vec{\jmath}$

lo que nos da el sistema de ecuaciones

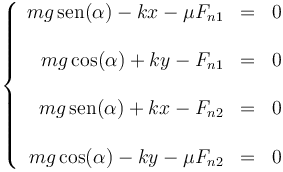
$\left\{\begin{array}{rcl} mg\,\mathrm{sen}(\alpha) - kx -\mu F_{n1}& = & 0 \\ && \\ mg\cos(\alpha) + ky - F_{n1} & = & 0 \\ && \\ mg\,\mathrm{sen}(\alpha) + kx -F_{n2} & = & 0 \\ && \\ mg\cos(\alpha) - ky -\mu F_{n2} & = & 0\end{array}\right.$

En forma numérica, en el SI

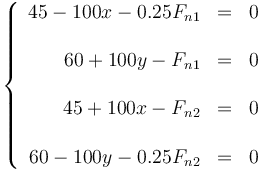
$\left\{\begin{array}{rcl} 45 - 100x -0.25 F_{n1}& = & 0 \\ && \\ 60 + 100y - F_{n1} & = & 0 \\ && \\ 45 + 100x -F_{n2} & = & 0 \\ && \\ 60 - 100y -0.25 F_{n2} & = & 0\end{array}\right.$

Este es un sistema de cuatro ecuaciones acopladas con cuatro incógnitas (a diferencia del caso sin rozamiento, que eran dos sistemas de dos ecuaciones; el rozamiento hace que la posición de cada masa influya sobre la otra, lo que antes no ocurría).

La solución de este sistema es sencilla por reducción o por otros métodos y el resultado es

$x =19\,\mathrm{cm}\qquad\qquad y = 44\,\mathrm{cm}\qquad \qquad F_{n1}=104\,\mathrm{N}\qquad\qquad F_{n2}=64\,\mathrm{N}$

4.2 Máxima longitud del resorte

Para el caso de máxima longitud operamos de la misma manera, solo que en este caso la fuerza de rozamiento va hacia abajo de los planos.

Archivo:dos-planos-inclinados-muelle-05.png

Por ello, el sistema de ecuaciones es ahora

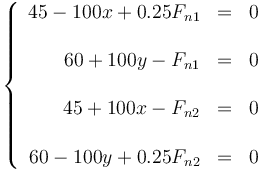
$\left\{\begin{array}{rcl} 45 - 100x +0.25 F_{n1}& = & 0 \\ && \\ 60 + 100y - F_{n1} & = & 0 \\ && \\ 45 + 100x -F_{n2} & = & 0 \\ && \\ 60 - 100y +0.25 F_{n2} & = & 0\end{array}\right.$

Operando de la misma manera obtenemos la solución

$x =83\,\mathrm{cm}\qquad\qquad y = 92\,\mathrm{cm}\qquad \qquad F_{n1}=152\,\mathrm{N}\qquad\qquad F_{n2}=128\,\mathrm{N}$

Podemos ver que en el primer caso obtenemos un valor para la posición menor que el de la posición de equilibrio sin rozamiento y en el segundo un valor mayor. También que la fuerza normal es muy superior al peso en el segundo caso, debido a que también debe contrarrestar la fuerza ejercida por el resorte.

Dos masas en planos inclinados y un muelle

De Laplace

Contenido

1 Enunciado

2 Posición de equilibrio

3 Fuerzas de reacción

4 Caso con rozamiento

4.1 Mínima longitud del resorte

4.2 Máxima longitud del resorte

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES