Entrar Página Discusión Historial Go to the site toolbox

Primera convocatoria 2017/18 (F2GIA)

De Laplace

(Diferencias entre revisiones)
(→Fuerza eléctrica en sistema de cuatro cargas puntuales)
(→Determinación del material de un cable conductor)
Línea 53: Línea 53:
# Haga una estimación de los valores de la intensidad del campo eléctrico  (<math>E=|\vec{E}|</math>), y de la densidad volumétrica (<math>J=|\vec{J}|</math>), en el interior del cable.
# Haga una estimación de los valores de la intensidad del campo eléctrico  (<math>E=|\vec{E}|</math>), y de la densidad volumétrica (<math>J=|\vec{J}|</math>), en el interior del cable.
 +
==[[Campo_magnético_en el plano de simetría de  dos_corrientes_filiformes_rectilíneas_(GIA)|Campo magnético en el plano de simetría de dos corrientes rectilíneas]]==
 +
 +
Dos conductores filiformes rectilíneos de longitud indefinida, <math>\Delta_1</math> y <math>\Delta_2</math>, están dispuestos en el plano
 +
<math>OXZ</math>, en paralelo al eje <math>OZ</math> y a igual distancia <math>a</math> de éste, de manera que pasan por los puntos <math>C_1(-a,0,0)</math> y <math>C_2(a,0,0)</math>, respectivamente. Los conductores soportan sendas corrientes eléctricas cuyas intensidades, <math>I_1</math> e <math>I_2</math>, son medidas por amperímetros que indican valores positivos si las corrientes recorren los hilos en el sentido de &ldquo;<math>z</math>&rdquo; creciente, y negativos si lo hacen en el sentido de &ldquo;<math>z</math>&rdquo;
 +
decreciente. Describa cómo es la dirección, el sentido y el módulo del
 +
campo magnético total en los puntos de coordenadas <math>P(0,y,z)</math> situados
 +
en el plano <math>\Pi_{{}_{OYZ}}:x=0</math> (plano cartesiano <math>OYZ</math>), en las siguientes situaciones:
 +
 +
# Las corrientes en los conductores son opuestas: <math>I_1=-I_2=I_0>0</math>.
 +
# Las corrientes en los conductores son iguales y descendentes: <math>I_1=I_2=-I_0<0</math>.
 +
 +
[[Archivo:f2_gIA_ex1ac_17_18_e6_0.png|center]]
[[Categoría: Problemas de examen F2 GIA]]
[[Categoría: Problemas de examen F2 GIA]]

Revisión de 00:19 20 jul 2018

Contenido

1 Fuerza eléctrica en sistema de cuatro cargas puntuales

Dos cargas eléctricas puntuales idénticas de valor Q, ocupan sendos puntos A y C que, en un sistema de referencia OXYZ, tienen coordenadas cartesianas A(a,0,0) y C( − a,0,0). Otras dos cargas idénticas entre sí y de valor q, ocupan los puntos B y D del eje OY, cuyas coordenadas cartesianas son B(0,b,0) y D(0, − b,0). La geometría

del sistema es tal que la distancia que separa dos carta contiguas es

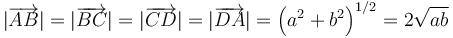
|\overrightarrow{AB}|=|\overrightarrow{BC}|=|\overrightarrow{CD}|=|\overrightarrow{DA}|=\left(a^2+b^2\right)^{1/2}=2 \sqrt{ab}

No existen más cargas eléctricas, a parte de las cuatro que constituyen el sistema descrito.

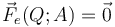  1. ¿Qué relación deben verificar la cantidades de Q y q de las respectivas cargas puntuales descritas en el sistema para que la fuerza eléctrica resultante que actúa sobre la carga que ocupa el punto A sea nula, \vec{F}_e(Q;A)=\vec{0}?
  2. En las condiciones del apartado anterior, ¿cómo es la fuerza eléctrica resultante que actúa sobre cada una de las otras tres cargas?

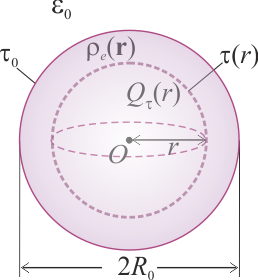
2 Campo eléctrico de distribución volumétrica de carga con simetría radial

En una esfera τ0 de radio R0 y centro en O, existe una distribución no uniforme de carga eléctrica negativa descrita por una densidad volumétrica radial ρe(r), respecto del punto O, de manera que r es la distancia desde dicho centro al punto P donde se mide la densidad de carga. Dicha distribución es tal que si consideramos una región esférica τ con centro en O y radio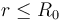 r\leq R_0, la cantidad parcial de carga contenida en τ es 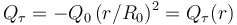Q_\tau=-Q_0\!\ (r/R_0)^2=Q_\tau(r). No hay más cargas en el sistema.
  1. ¿Cómo es la componente radial del campo eléctrico E(r) creado por la distribución descrita, tanto dentro como fuera de la esfera τ0?
  2. ¿Cómo es el potencial electrostático creado por la distribución en el exterior de τ0? ¿Cuánto vale el potencial en el centro O?


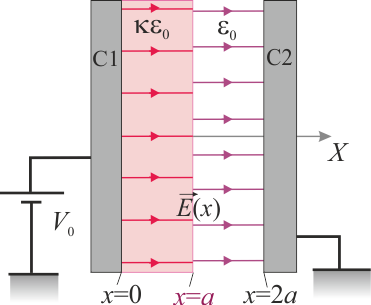
3 Potencial en sistema de conductores planos con medio inhomogéneo

Dos cuerpos conductores,C1 y C2, presentan sendas superficies planas, perpendiculares al eje OX, que coinciden con los planos geométricos Π1:x = 0 y con Π2:x = 2a. La distancia de separación, 2a, es significativamente menor que las dimensiones de los planos conductores. La región correspondiente a 0 < x < a está ocupada por un dieléctrico lineal de constante dieléctrica κ, mientras que la comprendida en el intervalo a < x < 2a está rellena de aire. El conductor C1 está conectado a un generador cuya f.e.m. tiene un valor constante V0, y el C2 a tierra. Esta diferencia de potencial entre los conductores determina la presencia de un campo eléctrico en la región dieléctrica que los separa, y cuya expresión es:


\vec{E}(x,y,z)=\left\{ \begin{array} {l} \displaystyle \frac{E_0}{\kappa}\, \vec{\imath}\mathrm{;}\;\;\;\mathrm{si}\;\; 0<x<a \\ \\ \\ \displaystyle E_0\ \vec{\imath}\mathrm{;}\;\;\;\mathrm{si}\;\; a<x<2a \end{array}\right.


  1. ¿Cómo son las superficies equipotenciales entre los dos conductores? Indique de qué forma varía el valor del potencial de dichas superficies.
  2. ¿Qué relación existe entre los valores V0 y E0? Obtenga la función V(x) que describe cómo es el valor del potencial en la región 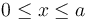0\leq x\leq a (dieléctrico lineal), y en 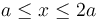a\leq x\leq 2a(aire).

4 Condensador plano paralelo

Se tienen dos discos conductores idénticos, de radio 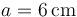a=6\,\mathrm{cm}, con los que se quiere construir un condensador plano-paralelo de capacidad eléctrica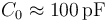 C_0\approx100\,\mathrm{pF}

  1. Si los conductores están separados por aire, cuyo campo de ruptura es 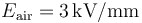E_\mathrm{air}=3\,\mathrm{kV/mm}, ¿qué distancia debe existir entre los discos conductores? ¿Cuál es el máximo valor de diferencia de potencial que puede aplicarse entre los discos?
  2. Si se separan por una lámina de papel de espesor 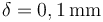\delta=0,1\,\mathrm{mm}, cuya constante de dieléctrica es 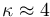\kappa\approx 4, y cuyo campo de ruptura es 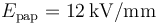E_\mathrm{pap}=12\,\mathrm{kV/mm}, ¿cuál será la capacidad eléctrica y la diferencia de potencial que puede aplicarse?

5 Determinación del material de un cable conductor

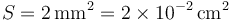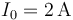Un conductor filiforme, de un material desconocido, tiene una sección uniforme de área S= 2\,\mathrm{mm}^2=2\times 10^{-2}\,\mathrm{cm}^2. Para determinar el tipo de material, se hace que por el hilo conductor circule una corriente estacionaria de intensidad I_0=2\,\mathrm{A} y, con la ayuda de un voltímetro, se determinan dos puntos A y B en el hilo tales que la diferencia de potencial entre ellos sea 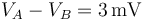V_A-V_B=3\,\mathrm{mV}. 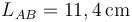Se determina que la longitud del hilo comprendida entre dichos puntos es L_{AB}=11,4\,\mathrm{cm}.

  1. Calcule la conductividad del hilo e indique de qué material está fabricado.
  2. Haga una estimación de los valores de la intensidad del campo eléctrico (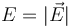E=|\vec{E}|), y de la densidad volumétrica (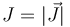J=|\vec{J}|), en el interior del cable.

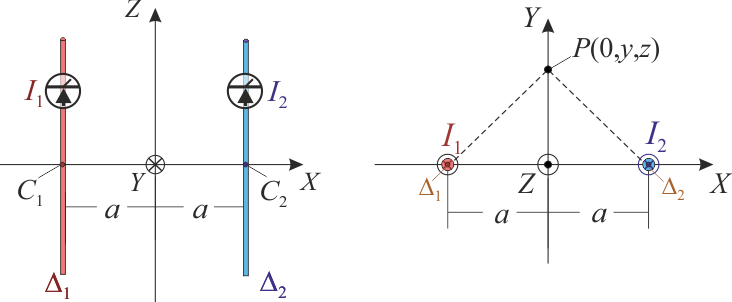
6 Campo magnético en el plano de simetría de dos corrientes rectilíneas

Dos conductores filiformes rectilíneos de longitud indefinida, Δ1 y Δ2, están dispuestos en el plano OXZ, en paralelo al eje OZ y a igual distancia a de éste, de manera que pasan por los puntos C1( − a,0,0) y C2(a,0,0), respectivamente. Los conductores soportan sendas corrientes eléctricas cuyas intensidades, I1 e I2, son medidas por amperímetros que indican valores positivos si las corrientes recorren los hilos en el sentido de “z” creciente, y negativos si lo hacen en el sentido de “z” decreciente. Describa cómo es la dirección, el sentido y el módulo del campo magnético total en los puntos de coordenadas P(0,y,z) situados en el plano 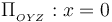\Pi_{{}_{OYZ}}:x=0 (plano cartesiano OYZ), en las siguientes situaciones:

  1. Las corrientes en los conductores son opuestas: I1 = − I2 = I0 > 0.
  2. Las corrientes en los conductores son iguales y descendentes: I1 = I2 = − I0 < 0.
Obtenido de "http://tesla.us.es/wiki/index.php/Primera_convocatoria_2017/18_(F2GIA)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace