Problemas de campo eléctrico (GIA)
De Laplace
(→Campo eléctrico en el eje de un hilo cargado y un disco) |
|||
| Línea 68: | Línea 68: | ||
# ¿Como se ve afectado la densidad de carga en la superficie exterior si la carga puntual no está en el centro de la cavidad? | # ¿Como se ve afectado la densidad de carga en la superficie exterior si la carga puntual no está en el centro de la cavidad? | ||
# Repetir los apartados anteriores en caso de que se añada una carga neta de <math>+3.5\mu C</math> a la corteza. | # Repetir los apartados anteriores en caso de que se añada una carga neta de <math>+3.5\mu C</math> a la corteza. | ||
| + | |||
| + | |||
| + | ==[[ Campo_eléctrico_en_el_eje_de_un_anillo| Campo eléctrico en el eje de un anillo, de una corona circular y de un disco ]]== | ||
| + | Halle el campo eléctrico en todos los puntos del eje de un anillo de radio <math>R</math> sobre el cual hay una densidad de carga uniforme <math>\lambda</math>. | ||
| + | |||
| + | A partir de este resultado, calcule el campo creado por una corona circular de radios <math>R_1</math> y <math>R_2</math> (<math>R_1<R_2</math>), sobre la cual hay una densidad de carga uniforme <math>\sigma_0</math>, en los puntos de su eje. | ||
| + | |||
| + | ¿A que se reduce si <math>R_1\to 0</math>? ¿Y si <math>R_2\to\infty</math>? Considere en particular el comportamiento en las proximidades de <math>z=0</math>. | ||
Revisión de 15:30 25 feb 2012
1 Carga total en un cubo de cobre
Se tiene un cubo de cobre de 1 cm de arista. Calcula la cantidad de carga positiva y negativa que hay en el cubo. Si en un instante dado, los dos tipos de carga se separasen ocupando cada uno una mitad del tubo, estima la aceleración que sufriría cada una de las mitades si el cubo se dividiera en ese instante.
Datos: Número atómico del cobre Z = 29, 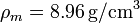 ,
, 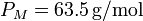 .
.
2 Densidades de carga eléctrica
Calcula la carga eléctrica total en cada uno de estos sistemas
- Uno hilo recto de longitud L con una densidad lineal de carga uniforme λ0.
- Un hilo recto de longitud L con densidad lineal de carga
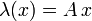 (x = 0 corresponde al punto medio).
(x = 0 corresponde al punto medio).
- Un hilo circular con densidad de carga lineal uniforme λ0.
- Un disco de radio R y grosor nulo con densidad superficial de carga uniforme σ0.
- Una esfera de radio R con densidad de carga volumétrica uniforme ρ0.
- Una esfera de radio R con densidad de carga volumétrica
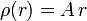 , siendo r la distancia al centro de la esfera.
, siendo r la distancia al centro de la esfera.
3 Electroscopio
Un electroscopio mide la carga por la desviación angular de dos esferas idénticas conductoras, suspendidas por cuerdas aislantes de masas despreciables y longitud L. Cada esfera tiene una masa m y está sometida a la gravedad g. Las cargas pueden considerarse como puntuales e iguales entre sí. Halla la ecuación que liga el semiángulo θ con el valor de la carga total Q depositada en las esferas.
Supón que la masa de cada esfera es 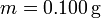 y la longitud del cable del que penden es
y la longitud del cable del que penden es 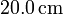 . Admite asimismo que los ángulos de desviación pueden medirse como mucho con una precisión de 1o. ¿Cuál es la carga mínima que puede medirse con este aparato? ¿Y la carga máxima?
. Admite asimismo que los ángulos de desviación pueden medirse como mucho con una precisión de 1o. ¿Cuál es la carga mínima que puede medirse con este aparato? ¿Y la carga máxima?
4 Campo eléctrico entre dos cargas puntuales
Se tienen dos cargas puntuales q1 y q2 separadas por una distancia d. Determina el punto sobre la línea que las une en el que el campo eléctrico se anula para cada uno de estos casos
-
 .
.
-
 .
.
-
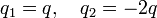 .
.
- q1 y q2 arbitrarios.
5 Campo eléctrico en el vértice de un cuadrado
En tres de los vértices de un cuadrado de lado 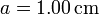 tenemos sendas cargas puntuales q1, q2 y q3. Calcula el campo eléctrico en el vértice sin carga en cada uno de los siguientes casos.
tenemos sendas cargas puntuales q1, q2 y q3. Calcula el campo eléctrico en el vértice sin carga en cada uno de los siguientes casos.
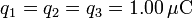 .
.
-
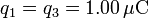 ,
, 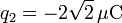 .
.
-
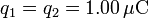 ,
, 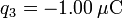 .
.
6 Campo eléctrico de un dipolo
Tenemos dos cargas puntuales de la misma magnitud y signo contrario separadas una distancia d.
- Encuentra la expresión que da el campo eléctrico en los puntos de la línea que une ambas cargas.
- Encuentra la expresión que da el campo eléctrico en los puntos de la línea perpendicular a la línea que une las dos carga y pasa por el punto equidistante entre ellas.
- En los dos casos anteriores, ¿cómo el es campo eléctrico cuando la distancia al punto medio es grande?
7 Fuerza sobre un dipolo
Se tiene un dipolo eléctrico 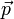 situado a una distancia x de un hilo infinito cargado uniformemente con densidad de carga uniforme λ0. Admitiendo que el dipolo está orientado en la dirección del campo creado por el hilo, encuentra la expresión de la fuerza que el hilo crea sobre el dipolo.
situado a una distancia x de un hilo infinito cargado uniformemente con densidad de carga uniforme λ0. Admitiendo que el dipolo está orientado en la dirección del campo creado por el hilo, encuentra la expresión de la fuerza que el hilo crea sobre el dipolo.
8 Campo eléctrico de un hilo cargado
Tenemos un hilo recto de longitud L cargado uniformemente con una carga total Q.
- Calcula el campo eléctrico en los puntos del plano perpendicular al hilo que pasa por su centro.
- Encuentra la expresión aproximada del campo en puntos muy alejados del hilo.
- Utiliza el primer apartado para calcular el campo eléctrico producido por un hilo infinito con densidad de carga lineal uniforme λ0 en todos los puntos del espacio.
9 Campo eléctrico en el eje de un hilo circular cargado y un disco
Se tiene un anillo circular de radio R y grosor despreciable. El anillo está cargado uniformemente con una carga total Q. Calcula el campo eléctrico en los puntos del eje central del anillo.
Usando este resultado, calcula el campo eléctrico en los puntos del eje central de un disco de radio R y espesor despreciable cargado uniformemente con densidad superficial uniforme σ0.
10 Cálculo de campo eléctrico usando la ley de Gauss
Utilizando la ley de Gauss calcula el campo eléctrico de las siguientes distribuciones de carga
- Un hilo inifnito con densidad de carga lineal uniforme λ0.
- Un plano infinito con densidad de carga superficial uniforme σ0.
- Dos planos infinitos paralelos separados una distancia d y con densidades superficiales de carga uniformes σ0 y − σ0.
- Una esfera de radio R con carga en su superficie distribuida uniformemente con densidad superficial σ0.
- Una esfera de radio R con carga en volumen distribuida uniformemente con densidad volumétrica ρ0.
- Una esfera de radio R con densidad volumétrica de carga
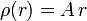 , siendo r la distancia al centro de la esfera.
, siendo r la distancia al centro de la esfera.
11 Carga puntual en un hueco conductor
Una carga puntual positiva de 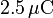 se sitúa en el centro de una corteza esférica de radio interior
se sitúa en el centro de una corteza esférica de radio interior 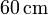 y radio exterior
y radio exterior 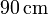 .
.
- Determina la expresión del campo eléctrico en todos los puntos del espacio.
- Determina las densidades superficiales de carga eléctrica en las superficies interior y exterior de la corteza, así como la carga total de esta.
- ¿Como se ve afectado la densidad de carga en la superficie exterior si la carga puntual no está en el centro de la cavidad?
- Repetir los apartados anteriores en caso de que se añada una carga neta de + 3.5μC a la corteza.
12 Campo eléctrico en el eje de un anillo, de una corona circular y de un disco
Halle el campo eléctrico en todos los puntos del eje de un anillo de radio R sobre el cual hay una densidad de carga uniforme λ.
A partir de este resultado, calcule el campo creado por una corona circular de radios R1 y R2 (R1 < R2), sobre la cual hay una densidad de carga uniforme σ0, en los puntos de su eje.
¿A que se reduce si 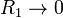 ? ¿Y si
? ¿Y si 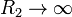 ? Considere en particular el comportamiento en las proximidades de z = 0.
? Considere en particular el comportamiento en las proximidades de z = 0.





