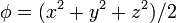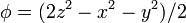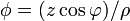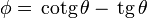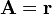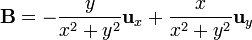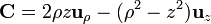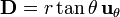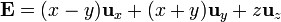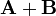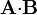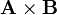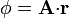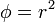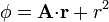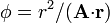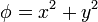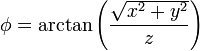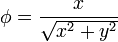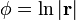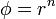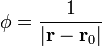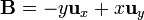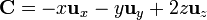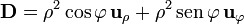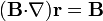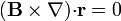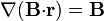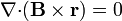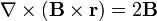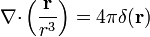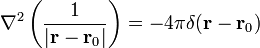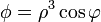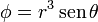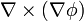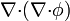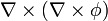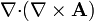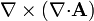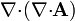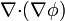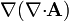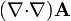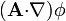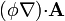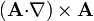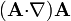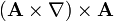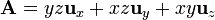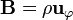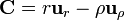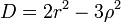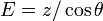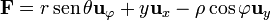Problemas de fundamentos matemáticos
De Laplace
(→{{nivel|2}} Cálculo de gradientes) |
|||
| (47 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | ==[[Campos escalares en diferentes sistemas]]== | + | =={{nivel|1}} [[Campos escalares en diferentes sistemas]]== |
Exprese los siguientes campos escalares en coordenadas cartesianas, cilíndricas y esféricas | Exprese los siguientes campos escalares en coordenadas cartesianas, cilíndricas y esféricas | ||
| Línea 5: | Línea 5: | ||
# <math>\phi = (2z^2-x^2-y^2)/2\,</math> | # <math>\phi = (2z^2-x^2-y^2)/2\,</math> | ||
# <math>\phi = (z\cos\varphi)/\rho</math> | # <math>\phi = (z\cos\varphi)/\rho</math> | ||
| - | # <math>\phi = \ | + | # <math>\phi = \,\mathrm{cotg}\,\theta - \,\mathrm{tg}\,\theta\,</math> |
| - | ==[[Campos vectoriales en diferentes sistemas]]== | + | [[Campos escalares en diferentes sistemas|'''Solución''']] |
| + | |||
| + | =={{nivel|2}} [[Campos vectoriales en diferentes sistemas]]== | ||
Exprese los siguientes campos vectoriales en coordenadas cartesianas, cilíndricas y esféricas: | Exprese los siguientes campos vectoriales en coordenadas cartesianas, cilíndricas y esféricas: | ||
| Línea 14: | Línea 16: | ||
# <math>\mathbf{C} = 2\rho z\mathbf{u}_{\rho}-(\rho^2-z^2)\mathbf{u}_{z}</math> | # <math>\mathbf{C} = 2\rho z\mathbf{u}_{\rho}-(\rho^2-z^2)\mathbf{u}_{z}</math> | ||
# <math>\mathbf{D}=r\tan\theta\,\mathbf{u}_{\theta}</math> | # <math>\mathbf{D}=r\tan\theta\,\mathbf{u}_{\theta}</math> | ||
| + | # <math>\mathbf{E} = (x-y)\mathbf{u}_{x}+(x+y)\mathbf{u}_{y}+z\mathbf{u}_{z}\,</math> | ||
| + | |||
| + | [[Campos vectoriales en diferentes sistemas|'''Solución''']] | ||
| + | |||
| + | =={{nivel|1}} [[Operaciones con vectores en diferentes sistemas]]== | ||
| + | Dados los vectores | ||
| + | |||
| + | <center><math>\mathbf{A} = \mathbf{u}_{\rho}-\mathbf{u}_{z}</math>{{qquad}} | ||
| + | <math>\mathbf{B} = 5\mathbf{u}_{r}+12\mathbf{u}_{\theta}</math></center> | ||
| + | |||
| + | evaluados en el punto de coordenadas cartesianas <math>x=3</math>, <math>y=4</math>, <math>z=12</math>, calcule | ||
| + | |||
| + | # <math>\mathbf{A}+\mathbf{B}\,</math> | ||
| + | #<math>\mathbf{A}{\cdot}\mathbf{B}\,</math> | ||
| + | #<math>\mathbf{A}\times\mathbf{B}\,</math> | ||
| + | |||
| + | [[Operaciones con vectores en diferentes sistemas|'''Solución''']] | ||
| - | ==[[Trazado de superficies equiescalares]]== | + | =={{nivel|1}} [[Trazado de superficies equiescalares]]== |
Describa las superficies equipotenciales de los siguientes campos escalares | Describa las superficies equipotenciales de los siguientes campos escalares | ||
| Línea 28: | Línea 47: | ||
donde <math>\mathbf{A}</math> es un vector constante y <math>\mathbf{r}</math> es el vector de posición. | donde <math>\mathbf{A}</math> es un vector constante y <math>\mathbf{r}</math> es el vector de posición. | ||
| - | ==[[Cálculo de gradientes]]== | + | =={{nivel|2}} [[Cálculo de gradientes]]== |
Para los campos escalares | Para los campos escalares | ||
| Línea 36: | Línea 55: | ||
calcule su gradiente en coordenadas cartesianas, cilíndricas y esféricas. | calcule su gradiente en coordenadas cartesianas, cilíndricas y esféricas. | ||
| - | ==[[Regla de la cadena para gradientes]]== | + | =={{nivel|2}} [[Regla de la cadena para gradientes]]== |
Si <math>\phi = \phi(u)\,</math>, con <math>u = u(\mathbf{r})</math>, demuestre que | Si <math>\phi = \phi(u)\,</math>, con <math>u = u(\mathbf{r})</math>, demuestre que | ||
| Línea 47: | Línea 66: | ||
# <math>\phi=\frac{1}{|\mathbf{r} -\mathbf{r}_0|}</math> | # <math>\phi=\frac{1}{|\mathbf{r} -\mathbf{r}_0|}</math> | ||
| - | ==[[Integral sobre una superficie esférica]]== | + | [[Regla de la cadena para gradientes|'''Solución''']] |
| + | |||
| + | =={{nivel|3}} [[Integral sobre una superficie esférica]]== | ||
Halle el valor de la integral | Halle el valor de la integral | ||
| Línea 58: | Línea 79: | ||
y la superficie de integración una esfera de radio <math>R</math> centrada en el origen. | y la superficie de integración una esfera de radio <math>R</math> centrada en el origen. | ||
| - | ==[[Cálculo de divergencias y rotacionales]]== | + | [[Integral sobre una superficie esférica|'''Solución''']] |
| + | |||
| + | =={{nivel|2}} [[Cálculo de divergencias y rotacionales]]== | ||
Para los campos vectoriales | Para los campos vectoriales | ||
| Línea 64: | Línea 87: | ||
#<math>\mathbf{B}=-y\mathbf{u}_{x}+x\mathbf{u}_{y}\,</math> | #<math>\mathbf{B}=-y\mathbf{u}_{x}+x\mathbf{u}_{y}\,</math> | ||
#<math>\mathbf{C} = -x\mathbf{u}_{x}-y\mathbf{u}_{y}+2z\mathbf{u}_{z}\,</math> | #<math>\mathbf{C} = -x\mathbf{u}_{x}-y\mathbf{u}_{y}+2z\mathbf{u}_{z}\,</math> | ||
| - | #<math>\mathbf{D} = \rho^2\cos\varphi\,\mathbf{u}_{\rho}+\rho^2\,\ | + | #<math>\mathbf{D} = \rho^2\cos\varphi\,\mathbf{u}_{\rho}+\rho^2\,\mathrm{sen}\,\varphi\,\mathbf{u}_{\varphi}</math> |
calcule su divergencia y su rotacional, empleando en cada caso, coordenadas cartesianas, cilíndricas y esféricas. ¿Cuáles son | calcule su divergencia y su rotacional, empleando en cada caso, coordenadas cartesianas, cilíndricas y esféricas. ¿Cuáles son | ||
irrotacionales y cuáles solenoidales? | irrotacionales y cuáles solenoidales? | ||
| - | ==[[Cálculo de flujo]]== | + | =={{nivel|2}} [[Cálculo de flujo]]== |
Para el campo vectorial | Para el campo vectorial | ||
| Línea 82: | Línea 105: | ||
En cada caso, halle el flujo por integración directa y por aplicación del teorema de Gauss. | En cada caso, halle el flujo por integración directa y por aplicación del teorema de Gauss. | ||
| - | ==[[Cálculo de circulación]]== | + | [[Cálculo de flujo|'''Solución''']] |
| + | |||
| + | =={{nivel|2}} [[Cálculo de circulación]]== | ||
Para el campo vectorial | Para el campo vectorial | ||
| Línea 89: | Línea 114: | ||
calcule su circulación a lo largo de las siguientes curvas cerradas: | calcule su circulación a lo largo de las siguientes curvas cerradas: | ||
| - | # Un cuadrado de lado <math>2a</math>, con vértices <math>\pm a\mathbf{u}_{x}\pm a\mathbf{u}_{y}</math>. | + | # Un cuadrado de lado <math>2a</math>, con vértices <math>\pm a\mathbf{u}_{x}\pm a\mathbf{u}_{y}</math>, siendo <math>+\mathbf{u}_z</math> el vector normal al cuadrado apoyado en el polígono. |
| - | # Una circunferencia de radio <math>R</math> situada en el plano <math>z=0</math> y con centro el origen de coordenadas. | + | # Una circunferencia de radio <math>R</math> situada en el plano <math>z=0</math> y con centro el origen de coordenadas, siendo <math>+\mathbf{u}_z</math> el vector normal al círculo limitado por la circunferencia. |
| - | # Una circunferencia vertical, situada en el plano <math>x=y</math> y con centro el origen de coordenadas. | + | # Una circunferencia vertical, situada en el plano <math>x=y</math> y con centro el origen de coordenadas, siendo <math>\mathbf{n}=\left(-\mathbf{u}_x+\mathbf{u}_y\right)/\sqrt{2}</math> el vector normal al círculo delimitado por la curva. |
En cada caso, halle la circulación por integración directa y por aplicación del teorema de Stokes. | En cada caso, halle la circulación por integración directa y por aplicación del teorema de Stokes. | ||
| - | ==[[ | + | [[Cálculo de circulación|'''Solución''']] |
| + | |||
| + | =={{nivel|3}} [[Algunas identidades vectoriales]]== | ||
Demuestre que si <math>\mathbf{r}</math> es el vector de posición y <math>\mathbf{B}</math> un campo vectorial arbitrario | Demuestre que si <math>\mathbf{r}</math> es el vector de posición y <math>\mathbf{B}</math> un campo vectorial arbitrario | ||
| Línea 102: | Línea 129: | ||
# <math>(\mathbf{B}\times\nabla)\times\mathbf{r}=-2\mathbf{B}</math> | # <math>(\mathbf{B}\times\nabla)\times\mathbf{r}=-2\mathbf{B}</math> | ||
| - | Igualmente, para el caso particular en que | + | Igualmente, para el caso particular en que <math>\mathbf{B}</math> represente un vector constante, demuestre que |
<ol start="4"> | <ol start="4"> | ||
<li><math>\nabla(\mathbf{B}{\cdot}\mathbf{r})=\mathbf{B}</math></li> | <li><math>\nabla(\mathbf{B}{\cdot}\mathbf{r})=\mathbf{B}</math></li> | ||
<li><math>\nabla{\cdot}(\mathbf{B}\times\mathbf{r})=0</math></li> | <li><math>\nabla{\cdot}(\mathbf{B}\times\mathbf{r})=0</math></li> | ||
| - | <li> | + | <li><math>\nabla\times(\mathbf{B}\times\mathbf{r})=2\mathbf{B}</math></li> |
</ol> | </ol> | ||
| + | [[Algunas identidades vectoriales|'''Solución''']] | ||
| + | |||
| + | =={{nivel|3}} [[Propiedades de la Delta de Dirac]]== | ||
| + | Se define la ''función'' delta de Dirac en tres dimensiones como aquella distribución que verifica | ||
| + | |||
| + | <center><math>\delta(\mathbf{r})=0</math>{{qquad}}<math>(\mathbf{r}\neq 0)</math>{{qquad}}{{qquad}}<math>\int \delta(\mathbf{r})\,\mathrm{d}\tau=1</math></center> | ||
| + | |||
| + | con la última integral extendida a todo el espacio. | ||
| + | |||
| + | Pruebe que: | ||
| + | |||
| + | # <math>\nabla{\cdot}\left(\displaystyle\frac{\mathbf{r}}{r^3}\right)=4\pi\delta(\mathbf{r})</math> | ||
| + | # <math>\nabla^2\left(\displaystyle\frac{1}{|\mathbf{r}-\mathbf{r}_0|}\right)= -4\pi\delta(\mathbf{r}-\mathbf{r}_0)</math> | ||
| + | |||
| + | =={{nivel|2}} [[Cálculo de laplacianos]]== | ||
| + | Calcule el laplaciano de los campos escalares | ||
| + | |||
| + | # <math>\phi = (x^2+y^2+z^2)/2\,</math> | ||
| + | # <math>\phi = (2z^2-x^2-y^2)/2\,</math> | ||
| + | # <math>\phi = \rho^3\cos\varphi</math> | ||
| + | # <math>\phi = r^3\,\mathrm{sen}\,\theta</math> | ||
| + | |||
| + | empleando coordenadas cartesianas, cilíndricas y esféricas. | ||
| + | |||
| + | [[Cálculo de laplacianos|'''Solución''']] | ||
| + | |||
| + | =={{nivel|3}} [[Cálculo de laplaciano vectorial]]== | ||
| + | Halle el laplaciano del campo vectorial | ||
| + | |||
| + | <center><math>\mathbf{A}=r^n\mathbf{r}\,</math></center> | ||
| + | |||
| + | [[Cálculo de laplaciano vectorial|'''Solución''']] | ||
| + | |||
| + | =={{nivel|4}} [[Vector superficie]]== | ||
| + | Demuestre que integrando alrededor de una curva cerrada, <math>\Gamma</math>, del plano <math>XY</math>, se cumple que | ||
| + | |||
| + | <center><math>\left|\frac{1}{2}\oint_{\Gamma} \mathbf{r} \times \mathrm{d}\mathbf{r}\,\right| = S</math></center> | ||
| + | |||
| + | donde <math>\mathbf{r}</math> es el vector de posición y <math>S</math> el área encerrada por <math>\Gamma</math>. | ||
| + | |||
| + | A partir de aquí, deduzca que para una curva arbitraria en el espacio | ||
| + | |||
| + | <center><math>\frac{1}{2}\oint\mathbf{r} \times \mathrm{d}\mathbf{r}= \mathbf{S}</math></center> | ||
| + | |||
| + | donde <math>\mathbf{S}</math> es un vector cuyas componentes son las áreas de las proyecciones de la curva sobre los planos | ||
| + | coordenados. | ||
| + | |||
| + | A partir del resultado anterior calcule el valor de <math>\mathbf{S}</math> para una curva formada por tres cuartos de circunferencia, que van respectivamente del punto <math>R\mathbf{u}_z</math> al <math>R\mathbf{u}_x</math>, de este a <math>R\mathbf{u}_y</math>, y de este de nuevo a <math>R\mathbf{u}_z</math>. | ||
| + | |||
| + | [[Vector superficie|'''Solución''']] | ||
| + | |||
| + | =={{nivel|3}} [[Campo de velocidades de un vórtice]]== | ||
| + | El campo de velocidades de un remolino puede aproximarse por la expresión, en cilíndricas, | ||
| + | |||
| + | <center><math>\mathbf{v}= \frac{C}{\rho}\mathbf{u}_{\varphi}</math></center> | ||
| + | |||
| + | # Demuestre que este campo es irrotacional en todos los puntos en los que está definido. | ||
| + | # Halle un potencial escalar del que derive este campo. | ||
| + | # ¿Cuanto vale la circulación del campo de velocidades a lo largo de una circunferencia en torno al eje <math>z</math>? ¿Qué consecuencias tiene esto para el potencial escalar? | ||
| + | |||
| + | =={{nivel|3}} [[Análisis de expresiones diferenciales]]== | ||
| + | De las siguientes expresiones | ||
| + | |||
| + | # <math>\nabla(\nabla{\cdot}\phi)</math> | ||
| + | # <math>\nabla\times(\nabla\phi)</math> | ||
| + | # <math>\nabla{\cdot}(\nabla{\cdot}\phi)</math> | ||
| + | # <math>\nabla\times(\nabla\times\phi)</math> | ||
| + | # <math>\nabla{\cdot}(\nabla\times\mathbf{A})</math> | ||
| + | # <math>\nabla\times(\nabla{\cdot}\mathbf{A})</math> | ||
| + | # <math>\nabla\times(\nabla\times\mathbf{A})</math> | ||
| + | # <math>\nabla{\cdot}(\nabla{\cdot}\mathbf{A})</math> | ||
| + | # <math>\nabla{\cdot}(\nabla\phi)</math> | ||
| + | # <math>\nabla(\nabla{\cdot}\mathbf{A})</math> | ||
| + | #<math>(\nabla{\cdot}\nabla)\mathbf{A}</math> | ||
| + | #<math>(\mathbf{A}{\cdot}\nabla)\phi</math> | ||
| + | #<math>(\phi\nabla){\cdot}\mathbf{A}</math> | ||
| + | #<math>(\mathbf{A}{\cdot}\nabla)\times\mathbf{A}</math> | ||
| + | #<math>(\mathbf{A}{\cdot}\nabla)\mathbf{A}</math> | ||
| + | #<math>(\mathbf{A}\times\nabla)\times\mathbf{A}</math> | ||
| + | |||
| + | (donde <math>\phi\,</math> es un cierto campo escalar y <math>\mathbf{A}</math> uno vectorial) indique cuáles son absurdas. De las que tienen sentido, señale las que son idénticamente nulas. De las que no son nulas, calcule su valor para los campos | ||
| + | |||
| + | <center><math>\phi=xyz\,</math>{{qquad}}<math>\mathbf{A}=x^2\mathbf{u}_{x}+xz\mathbf{u}_{y}-xy\mathbf{u}_{z}</math></center> | ||
| + | |||
| + | =={{nivel|3}} [[Análisis de diferentes campos]]== | ||
| + | De los siguientes campos, indique cuales son solenoidales, cuáles son irrotacionales y cuáles armónicos | ||
| + | |||
| + | # <math>\mathbf{A} = yz \mathbf{u}_{x} + xz \mathbf{u}_{y} + xy \mathbf{u}_{z}</math> | ||
| + | # <math>\mathbf{B} = \rho\mathbf{u}_{\varphi}</math> | ||
| + | #<math>\mathbf{C} = r\mathbf{u}_{r}-\rho\mathbf{u}_{\rho}</math> | ||
| + | #<math>D = 2r^2-3\rho^2\,</math> | ||
| + | #<math>E= z/\cos\theta\,</math> | ||
| + | #<math>\mathbf{F} = r\,\mathrm{sen}\,\theta\mathbf{u}_{\varphi}+y\mathbf{u}_{x}-\rho\cos\varphi\mathbf{u}_{y}</math> | ||
| - | [[Categoría:Problemas de fundamentos matemáticos]] | + | [[Categoría:Problemas de fundamentos matemáticos|0]] |
| + | [[Categoría:Fundamentos matemáticos]] | ||
| + | [[Categoría:Problemas de Campos Electromagnéticos|10]] | ||
última version al 10:28 16 nov 2009
1  Campos escalares en diferentes sistemas
Campos escalares en diferentes sistemas
Exprese los siguientes campos escalares en coordenadas cartesianas, cilíndricas y esféricas
2  Campos vectoriales en diferentes sistemas
Campos vectoriales en diferentes sistemas
Exprese los siguientes campos vectoriales en coordenadas cartesianas, cilíndricas y esféricas:
3  Operaciones con vectores en diferentes sistemas
Operaciones con vectores en diferentes sistemas
Dados los vectores
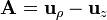
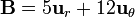
evaluados en el punto de coordenadas cartesianas x = 3, y = 4, z = 12, calcule
4  Trazado de superficies equiescalares
Trazado de superficies equiescalares
Describa las superficies equipotenciales de los siguientes campos escalares
donde  es un vector constante y
es un vector constante y  es el vector de posición.
es el vector de posición.
5  Cálculo de gradientes
Cálculo de gradientes
Para los campos escalares
calcule su gradiente en coordenadas cartesianas, cilíndricas y esféricas.
6  Regla de la cadena para gradientes
Regla de la cadena para gradientes
Si 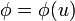 , con
, con 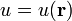 , demuestre que
, demuestre que
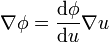
Encuentre 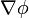 si
si
7  Integral sobre una superficie esférica
Integral sobre una superficie esférica
Halle el valor de la integral
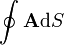
con
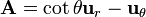
y la superficie de integración una esfera de radio R centrada en el origen.
8  Cálculo de divergencias y rotacionales
Cálculo de divergencias y rotacionales
Para los campos vectoriales
calcule su divergencia y su rotacional, empleando en cada caso, coordenadas cartesianas, cilíndricas y esféricas. ¿Cuáles son irrotacionales y cuáles solenoidales?
9  Cálculo de flujo
Cálculo de flujo
Para el campo vectorial
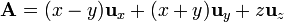
calcule su flujo a través de las siguientes superficies cerradas:
- Un cubo de arista a, con un vértice en el origen y aristas
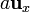 ,
, 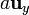 y
y 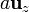 .
.
- Un cilindro circular de altura h y radio R, con el eje Z como eje y sus bases situadas en z = 0 y z = h.
- Una esfera de radio R en torno al origen de coordenadas.
En cada caso, halle el flujo por integración directa y por aplicación del teorema de Gauss.
10  Cálculo de circulación
Cálculo de circulación
Para el campo vectorial
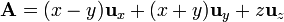
calcule su circulación a lo largo de las siguientes curvas cerradas:
- Un cuadrado de lado 2a, con vértices
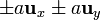 , siendo
, siendo 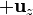 el vector normal al cuadrado apoyado en el polígono.
el vector normal al cuadrado apoyado en el polígono.
- Una circunferencia de radio R situada en el plano z = 0 y con centro el origen de coordenadas, siendo
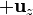 el vector normal al círculo limitado por la circunferencia.
el vector normal al círculo limitado por la circunferencia.
- Una circunferencia vertical, situada en el plano x = y y con centro el origen de coordenadas, siendo
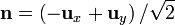 el vector normal al círculo delimitado por la curva.
el vector normal al círculo delimitado por la curva.
En cada caso, halle la circulación por integración directa y por aplicación del teorema de Stokes.
11  Algunas identidades vectoriales
Algunas identidades vectoriales
Demuestre que si  es el vector de posición y
es el vector de posición y  un campo vectorial arbitrario
un campo vectorial arbitrario
Igualmente, para el caso particular en que  represente un vector constante, demuestre que
represente un vector constante, demuestre que
12  Propiedades de la Delta de Dirac
Propiedades de la Delta de Dirac
Se define la función delta de Dirac en tres dimensiones como aquella distribución que verifica
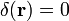
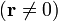
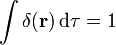
con la última integral extendida a todo el espacio.
Pruebe que:
13  Cálculo de laplacianos
Cálculo de laplacianos
Calcule el laplaciano de los campos escalares
empleando coordenadas cartesianas, cilíndricas y esféricas.
14  Cálculo de laplaciano vectorial
Cálculo de laplaciano vectorial
Halle el laplaciano del campo vectorial
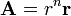
15  Vector superficie
Vector superficie
Demuestre que integrando alrededor de una curva cerrada, Γ, del plano XY, se cumple que
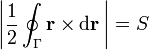
donde  es el vector de posición y S el área encerrada por Γ.
es el vector de posición y S el área encerrada por Γ.
A partir de aquí, deduzca que para una curva arbitraria en el espacio
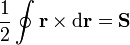
donde 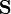 es un vector cuyas componentes son las áreas de las proyecciones de la curva sobre los planos
coordenados.
es un vector cuyas componentes son las áreas de las proyecciones de la curva sobre los planos
coordenados.
A partir del resultado anterior calcule el valor de 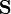 para una curva formada por tres cuartos de circunferencia, que van respectivamente del punto
para una curva formada por tres cuartos de circunferencia, que van respectivamente del punto 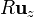 al
al 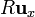 , de este a
, de este a 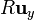 , y de este de nuevo a
, y de este de nuevo a 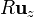 .
.
16  Campo de velocidades de un vórtice
Campo de velocidades de un vórtice
El campo de velocidades de un remolino puede aproximarse por la expresión, en cilíndricas,
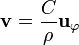
- Demuestre que este campo es irrotacional en todos los puntos en los que está definido.
- Halle un potencial escalar del que derive este campo.
- ¿Cuanto vale la circulación del campo de velocidades a lo largo de una circunferencia en torno al eje z? ¿Qué consecuencias tiene esto para el potencial escalar?
17  Análisis de expresiones diferenciales
Análisis de expresiones diferenciales
De las siguientes expresiones
(donde  es un cierto campo escalar y
es un cierto campo escalar y  uno vectorial) indique cuáles son absurdas. De las que tienen sentido, señale las que son idénticamente nulas. De las que no son nulas, calcule su valor para los campos
uno vectorial) indique cuáles son absurdas. De las que tienen sentido, señale las que son idénticamente nulas. De las que no son nulas, calcule su valor para los campos
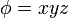
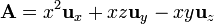
18  Análisis de diferentes campos
Análisis de diferentes campos
De los siguientes campos, indique cuales son solenoidales, cuáles son irrotacionales y cuáles armónicos