Problemas de materiales magnéticos
De Laplace
(→{{nivel|1}} Cálculo de corrientes de magnetización equivalentes) |
(→{{nivel|3}} Imán cilíndrico) |
||
| Línea 26: | Línea 26: | ||
# Halle la distribución de cargas magnéticas equivalentes y el problema de ecuaciones y condiciones de contorno para <math>\mathbf{H}</math>. | # Halle la distribución de cargas magnéticas equivalentes y el problema de ecuaciones y condiciones de contorno para <math>\mathbf{H}</math>. | ||
| - | =={{nivel| | + | =={{nivel|4}} [[Imán cilíndrico]]== |
Se construye un imán cilíndrico de radio <math>R=1\mathrm{cm}</math> y longitud <math>L</math>, con una magnetización uniforme y paralela a su eje <math>M_0=10^5\mathrm{A}/\mathrm{m}</math>. | Se construye un imán cilíndrico de radio <math>R=1\mathrm{cm}</math> y longitud <math>L</math>, con una magnetización uniforme y paralela a su eje <math>M_0=10^5\mathrm{A}/\mathrm{m}</math>. | ||
Revisión de 13:04 31 mar 2009
Contenido |
1 
Máxima imanación del hierro
El momento dipolar magnético de un átomo de hierro es aproximadamente
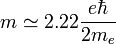
¿Cuál es el valor máximo que puede tener la magnetización de un trozo de hierro?
Suponga que se tiene un imán cilíndrico de gran longitud, magnetizado a lo largo de su eje. Sabiendo que el campo en el extremo de la barra es aproximadamente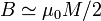 
, calcule el campo que producirá este imán. Estime el valor de las corrientes de magnetización equivalentes a esta imanación.
2 Cálculo de corrientes y cargas de magnetización
Se tiene un cilindro de longitud L y radio R, magnetizado según la ley
estando situado el origen de coordenadas en el centro del cilindro y siendo el eje z coincidente con el del imán.
- Halle las fuentes vectoriales equivalentes a esta magnetización.
- Calcule también la distribución de fuentes escalares equivalente.
3 
Imán esférico
Se dispone de una esfera de radio R con una imanación permanente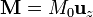 
.
- Determine la expresión integral del potencial vector magnético. Calcule el valor de la integral. Hállese, a partir de
, el valor de 
y de 
en todos los puntos del espacio.
- Describa cualitativamente la forma de , y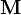
- Calcule las corrientes de magnetización equivalentes, las ecuaciones y las condiciones de contorno para .
- Halle la distribución de cargas magnéticas equivalentes y el problema de ecuaciones y condiciones de contorno para .
4 
Imán cilíndrico
Se construye un imán cilíndrico de radio R = 1cm y longitud L, con una magnetización uniforme y paralela a su eje M0 = 105A / m.
- Determine aproximadamente los campos y cuando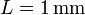
, en el centro del imán y en un punto ligeramente por encima de su base superior.
- A partir de las corrientes de magnetización.
- A partir de las cargas magnéticas.
- Estime y cuando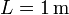
en los mismos puntos y con los mismos métodos
- Determine exactamente y en todos los puntos del eje del imán, tanto dentro como fuera de él. Compare con los resultados anteriores
5 
Campo de un cable bimetalico
Entre los distintos tipos de cable empleados en la industria, se encuentra el de \emph{aluminio revestido de cobre}. Está formado por un núcleo de aluminio de radio a (suponga a = 2mm), rodeado por una capa de cobre, de radio exterior b (sea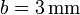 
).
Halle el campo magnético producido por el cable, tanto en su interior como su exterior, cuando por él circula una corriente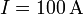 
. ¿Cuál es el valor máximo del campo magnético? ¿Dónde se alcanza?
6 Partícula magnética en un campo externo
Supóngase que se tiene una esfera de radio R un material magnético lineal (de permeabilidad μ) alrededor de la cual hay vacío. En puntos alejados de la esfera hay impuesto un campo magnético uniforme 
.
- Sabiendo que la magnetización que aparece en la esfera es uniforme, halle el valor de dicha magnetización, del momento dipolar inducido en la esfera, y del campo magnético en todos los puntos del espacio.
- ¿En qué se diferencia el resultado para un material diamagnético de uno paramagnético? ¿A qué se reducen los resultados en los casos de un paramagnético ideal (
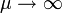) y un superconductor (μ = 0)?
- Halle las corrientes de magnetización que aparecen en la esfera.
- Calcule los valores numéricos para los apartados anteriores con un campo externo B0 = 10mT aplicado sobre una esfera de radio 1 cm para los siguientes materiales: oro, aluminio, hierro y un superconductor.
7 
Levitación de un imán
Los imanes pueden levitar cuando se encuentran frente a un superconductor. Para verlo, considere un pequeña esfera de momento magnético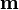 
y peso P situada frente a un plano infinito superconductor (μ = 0). El imán se encuentra a una altura z0 y su momento magnético apunta en la dirección perpendicular al plano superconductor.
- Determine el campo magnético en todos los puntos del espacio. (Sugerencia: Considérese un dipolo imagen)
- Aplicando la expresión de la fuerza entre dos dipolos magnéticos, calcule la fuerza sobre el dipolo situado sobre el plano. ¿Hacia donde se dirige esa fuerza?
- Halle la altura de equilibrio del imán sobre el plano.
- ¿Cómo cambian los resultados si el dipolo apunta paralelamente al plano?
