Máxima imanación del hierro

De Laplace

1 Enunciado

El momento dipolar magnético de un átomo de hierro es aproximadamente

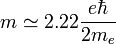
¿Cuál es el valor máximo que puede tener la magnetización de un trozo de hierro?

Suponga que se tiene un imán cilíndrico de gran longitud, magnetizado a lo largo de su eje. Sabiendo que el campo en el extremo de la barra es aproximadamente 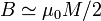, calcule el campo que producirá este imán. Estime el valor de las corrientes de magnetización equivalentes a esta imanación.

2 Campo magnético

Si el momento dipolar de cada átomo es 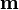, la magnetización, supuesto que todos los dipolos están orientados en el mismo sentido, será

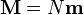
siendo N el número de átomos por unidad de volumen. Éste lo obtenemos, a su vez, conociendo la densidad de masa del hierro y la masa de cada átomo. Resulta

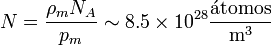
con lo que la magnetización máxima es

A esta magnetización le corresponde un campo magnético en el extremo del imán de aproximadamente

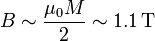
Este campo es realmente intenso. En la práctica no se suelen conseguir campos tan fuertes porque no todos los dipolos apuntan en el mismo sentido. Un trozo de hierro normal está constituido por dominios microscópicos. En cada uno de estos dominios sí hay una orientación determinada de todos sus dipolos, pero a escala macroscópica hay tantos dominios en una dirección como en la contraria, por lo que sus efectos se anulan. Cuando se consigue una orientación en un trozo de material es cuando se dice que tenemos un imán.

3 Corrientes de magnetización

Para hacerse una idea de lo que representa realmente la magnitud de este campo magnético podemos calcular las corrientes de magnetización equivalentes. En el caso de un imán cilíndrico con una imanación longitudinal no hay corrientes de magnetización de volumen, pero si de superficie.

        

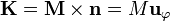
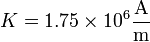
esto es, si con hilo de 1 mm de diámetro quisiéramos construir una bobina para conseguir el mismo campo deberíamos hacer circular una corriente de 1750 amperios por el hilo, lo que lo fundiría inmediatamente.