Cálculo de corrientes y cargas de magnetización

De Laplace

Contenido

1 Enunciado
2 Corrientes de magnetización
- 2.1 De volumen
- 2.2 Superficiales
3 Cargas magnéticas
- 3.1 De volumen
- 3.2 De superficie

1 Enunciado

Se tiene un cilindro de longitud $L$ y radio $R$ , magnetizado según la ley

$\mathbf{M}=Ay\mathbf{u}_{x}$

estando situado el origen de coordenadas en el centro del cilindro y siendo el eje $z$ coincidente con el del imán.

Halle las fuentes vectoriales equivalentes a esta magnetización.
Calcule también la distribución de fuentes escalares equivalente.

2 Corrientes de magnetización

Las densidades vectoriales equivalentes son las corrientes de magnetización, expresables como

$\mathbf{J}_m=\nabla\times\mathbf{M}$ $\mathbf{K}_m=\mathbf{n}\times[\mathbf{M}]$

2.1 De volumen

La densidad de corriente de volumen vale, en el interior,

$\mathbf{J}_m=\nabla\times\mathbf{M}=\left|\begin{matrix}\mathbf{u}_{x} & \mathbf{u}_{y} & \mathbf{u}_{z} \\ & & \\ \displaystyle\frac{\partial{}\ }{\partial x} & \displaystyle\frac{\partial{}\ }{\partial y} & \displaystyle\frac{\partial{}\ }{\partial z} \\ & & \\ Ay & 0 & 0\end{matrix}\right|=-A\mathbf{u}_{z}$

Resulta una densidad de corriente uniforme en la dirección vertical. En el exterior la densidad es nula, por serlo la imanación.

2.2 Superficiales

Para las densidades superficiales tenemos, en la cara superior

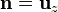
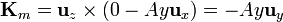
$\mathbf{n}=\mathbf{u}_{z}\,$ $\mathbf{K}_m=\mathbf{u}_{z}\times(0-A y \mathbf{u}_{x})=-Ay\mathbf{u}_{y}$

y en la inferior

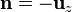
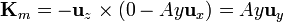
$\mathbf{n}=-\mathbf{u}_{z}\,$ $\mathbf{K}_m=-\mathbf{u}_{z}\times(0-A y \mathbf{u}_{x})=Ay\mathbf{u}_{y}$

Por último, en la cara lateral se verifica

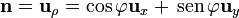
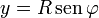
$\mathbf{n}=\mathbf{u}_{\rho}=\cos\varphi\mathbf{u}_{x}+\,\mathrm{sen}\,\varphi\mathbf{u}_{y}$ $y=R\,\mathrm{sen}\,\varphi$ $\mathbf{K}_m=(\cos\varphi\mathbf{u}_{x}+\,\mathrm{sen}\,\varphi\mathbf{u}_{y})\times(0-AR\,\mathrm{sen}\,\varphi\mathbf{u}_{x})=AR\,\mathrm{sen}^2\varphi\mathbf{u}_{z}$

Las líneas de corriente, que para la magnetización deben ser cerradas, van en la dirección vertical hacia abajo por el interior del imán, en la base inferior fluyen hacia la cara lateral, por la que suben y se cierra el circuito en la cara superior.

3 Cargas magnéticas

Las fuentes escalares equivalentes a la magnetización son las densidades de carga de magnetización, dadas por las expresiones

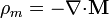
$\rho_m=-\nabla{\cdot}\mathbf{M}$ $\sigma_m=-\mathbf{n}{\cdot}[\mathbf{M}]$

3.1 De volumen

La densidad de carga de volumen es nula ya que, en el interior del cilindro,

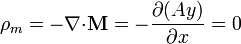
$\rho_m=-\nabla{\cdot}\mathbf{M}=-\frac{\partial{}(Ay)}{\partial x}=0$

y en el exterior la magnetización es nula.

3.2 De superficie

Las únicas cargas pueden estar en la superficie del cilindro. En las bases esta densidad de carga es cero, ya que la normal (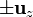 $\pm\mathbf{u}_{z}$ ) es ortogonal a la magnetización. En la cara lateral tenemos

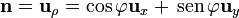
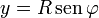
$\mathbf{n}=\mathbf{u}_{\rho}=\cos\varphi\mathbf{u}_{x}+\,\mathrm{sen}\,\varphi\mathbf{u}_{y}$ $y=R\,\mathrm{sen}\,\varphi$ $\sigma_m=-\mathbf{n}{\cdot}[\mathbf{M}]=-\left(\cos\varphi\mathbf{u}_{x}+\,\mathrm{sen}\,\varphi\mathbf{u}_{y}\right){\cdot}(0-AR\,\mathrm{sen}\,\varphi\mathbf{u}_{x})=AR\,\mathrm{sen}\,\varphi\cos\varphi=\frac{AR\,\mathrm{sen}\,(2\varphi)}{2}$

Esta densidad de carga es nula en 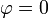$\varphi=0$ , $π / 2$ , $π$ y $3π / 2$ y positiva en el primer y tercer cuadrante y negativa en el segundo y el cuarto.

Cálculo de corrientes y cargas de magnetización

De Laplace

Contenido

1 Enunciado

2 Corrientes de magnetización

2.1 De volumen

2.2 Superficiales

3 Cargas magnéticas

3.1 De volumen

3.2 De superficie

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES