Problemas de Movimiento relativo (MR G.I.C.)
De Laplace
(Página creada con '=Problemas del boletín= == Giro de un triedro == right Los triedros <math>O_1X_1Y_1Z_1</math> y <math>OX_0Y_0Z_0</math…') |
|||
| Línea 31: | Línea 31: | ||
[[Imagen:disco_en_disco.gif|right]] | [[Imagen:disco_en_disco.gif|right]] | ||
En la figura se muestra un disco de radio <math>R</math> (sólido "2"), que gira con velocidad angular <math>\omega_{20}(t)=\omega</math>, constante, alrededor del eje perpendicular a él, <math>O_1X_0</math>. Dicho eje está rígidamente unido a una plataforma (sólido "0"), que gira también con velocidad angular constante <math>\omega_{01}(t)=\Omega</math>, alrededor del eje vertical <math>O_1Z_1</math> de un sistema de referencia fijo <math>O_1X_1Y_1Z_1</math> (sólido "1"). Determina las magnitudes cinemáticas <math>\vec{v}^B_{21}</math> y <math>\vec{a}^B_{21}</math> en el instante representado en la figura. | En la figura se muestra un disco de radio <math>R</math> (sólido "2"), que gira con velocidad angular <math>\omega_{20}(t)=\omega</math>, constante, alrededor del eje perpendicular a él, <math>O_1X_0</math>. Dicho eje está rígidamente unido a una plataforma (sólido "0"), que gira también con velocidad angular constante <math>\omega_{01}(t)=\Omega</math>, alrededor del eje vertical <math>O_1Z_1</math> de un sistema de referencia fijo <math>O_1X_1Y_1Z_1</math> (sólido "1"). Determina las magnitudes cinemáticas <math>\vec{v}^B_{21}</math> y <math>\vec{a}^B_{21}</math> en el instante representado en la figura. | ||
| + | |||
| + | ==[[Disco_y_varilla_con_dos_rotaciones | Disco y varilla con dos rotaciones ]]== | ||
| + | [[Imagen:disco_y_varilla.gif|right]] | ||
| + | El sistema de la figura está formado por una varilla <math>AB</math> de longitud <math>l</math> (sólido "0"), cuyo | ||
| + | extremo <math>A</math> está fijado en el eje vertical <math>O_1Z_1</math>, a una altura <math>R</math> sobre el plano horizontal fijo | ||
| + | <math>O_1X_1Y_1</math> (sólido "1"). La varilla <math>AB</math> gira alrededor de <math>O_1Z_1</math> con una velocidad angular | ||
| + | constante <math>\Omega</math>, permaneciendo siempre perpendicular a dicho eje vertical fijo. El extremo <math>B</math> | ||
| + | del sólido "0" está articulado al centro de un disco de radio <math>R</math> (sólido "2"), de modo que la | ||
| + | varilla es siempre perpendicular al disco. El disco gira con una velocidad angular constante | ||
| + | <math>\omega</math>, coincidiendo su eje de giro con la varilla. | ||
| + | #Caracterice los movimientos {01}, {20} y {21} (reducciones cinemáticas). | ||
| + | #Obtenga la expresión de la velocidad <math>\vec{v}^C_{21}</math> del punto de contacto del disco con el plano fijo <math>O_1X_1Y_1</math>, (punto <math>C</math>) en términos de los datos del problema. ¿Qué relación debe existir entre las velocidades angulares <math>\omega</math> y <math>\Omega</math> para que el disco ruede sin deslizar sobre el plano? | ||
| + | #Obtenga las expresiones de la aceleración angular del movimiento {21} y de la aceleración <math>\vec{a}^B_{21}</math> del centro del disco (punto <math>B</math>). Calcule la aceleración del punto de contacto <math>C</math> perteneciente al disco cuando éste rueda sin deslizar sobre el plano <math>O_1X_1Y_1</math>. | ||
| + | |||
| + | ==[[Ejercicio de cinemática del sólido rígido y movimiento relativo, Enero 2012|Cono rodando sin deslizar sobre plano]]== | ||
| + | Un cono recto de radio <math>R</math> en su base y una altura | ||
| + | <math>h=\sqrt{3}\,R</math> (sólido “2”), se mueve rodando sin deslizar sobre el plano fijo <math>O_1X_1Y_1</math> (sólido “1”), en el cuál apoya, en cada instante, una generatriz <math>\overline{OG}</math>. La velocidad del centro <math>C</math> de la base del cono, medida desde el sistema de referencia ligado al sólido “1”, tiene módulo constante de valor <math>v_0</math>. Para facilitar la descripción del movimiento, se introduce un sistema de referencia <math>OX_0Y_0Z_0</math> (sólido “0”) con origen <math>O</math> en el vértice del cono, el eje <math>OZ_0</math> siempre perpendicular al plano fijo “1”, y cuyo eje <math>OY_0</math> contiene en cada instante a la generatriz del cono en contacto con dicho plano. | ||
| + | |||
| + | <center>[[Archivo:cono_sobre_plano_0.gif]]</center> | ||
| + | |||
| + | # Reducciones cinematicas de los movimientos relativos. | ||
| + | # Ejes de rotación y naturaleza de los movimientos. | ||
| + | # Campos de aceleraciones. | ||
| + | |||
| + | == Enunciado == | ||
| + | [[Imagen:horquilla_y_disco_b.gif|right]] | ||
| + | El sistema de la figura consiste en una horquilla semicircular (sólido "0"), que siempre está paralela al plano fijo <math>O_1X_1Y_1</math> (sólido "1"). El punto <math>O</math> de dicho aro (siempre el mismo) se desplaza con velocidad <math>v</math> sobre el eje <math>O_1Z_1</math>, a la vez que el aro gira con velocidad angular constante <math>\Omega</math> alrededor de dicho eje fijo. Un disco de radio <math>R</math> (sólido "2"), se mueve respecto a "0" girando alrededor del diámetro común <math>AB</math>, con velocidad angular constante <math>\omega</math>. | ||
| + | |||
| + | '''Nota:''' Los valores de <math>\Omega</math>, <math>\omega</math> y <math>v</math> pueden ser positivos o negativos. | ||
| + | |||
| + | #¿Cuándo es nula la velocidad mínima del movimiento {21}? | ||
| + | #Qué debe ocurrir para que el eje instantáneo de rotación y mínimo deslizamiento pase por el centro del disco? Calcule en este caso la derivada temporal de la reducción cinemática | ||
| + | #¿Qué condición debe cumplirse para que el movimiento {21} sea una rotación instantánea y el eje instantáneo de rotación pase por el centro del disco? | ||
| + | |||
| + | |||
| + | |||
| + | ==[[ Partícula en tubo que gira (sistema no inercial) (G.I.A.) | Partícula en tubo que gira (ecuaciones de movimiento) ]]== | ||
| + | [[Archivo:bol_05_11_12_p_05.gif|right]]Una partícula de masa <math>m</math> se encuentra en el interior de un tubo estrecho, el cual gira con velocidad angular uniforme <math>\omega</math> en torno a un eje perpendicular al del tubo. Obtenga las ecuaciones de movimiento para la partícula aplicando los resultados del movimiento relativo de sólidos rígidos. | ||
Revisión de 18:25 30 sep 2015
Contenido |
1 Problemas del boletín
1.1 Giro de un triedro
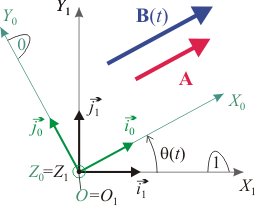
Los triedros O1X1Y1Z1 y OX0Y0Z0 están definidos de modo que sus orígenes y los ejes O1Z1 coinciden. El triedro "1" está en reposo y el triedro "0" gira respecto al "1" con velocidad angular uniforme 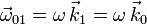 , de modo que el ángulo θ indicado en la figura es
, de modo que el ángulo θ indicado en la figura es 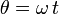 .
.
- Calcula las derivadas de los vectores de la base del triedro "0" vistos desde el triedro "1".
- Dado el vector
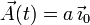 calcula
calcula

- Expresa el resultado en los vectores de la base móvil (triedro "0") y la base fija (triedro "1").
- Haz el mismo cálculo para el vector
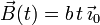
1.2 Coche sobre una plataforma circular
Una plataforma circular gira alrededor de un eje perpendicular a ella que pasa por su centro con velocidad angular uniforme ω. Un coche se mueve radialmente desde el centro de la plataforma hacia fuera con velocidad uniforme vc. Encuentra la expresión de la velocidad del coche visto desde la plataforma y desde un observador en reposo absoluto. Describe las trayectorias que describe el coche para cada uno de estos observadores.
Ayuda

1.3 Disco engarzado en otro disco
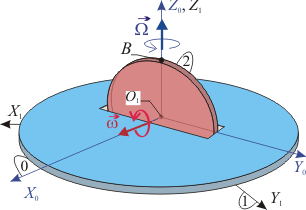
En la figura se muestra un disco de radio R (sólido "2"), que gira con velocidad angular ω20(t) = ω, constante, alrededor del eje perpendicular a él, O1X0. Dicho eje está rígidamente unido a una plataforma (sólido "0"), que gira también con velocidad angular constante ω01(t) = Ω, alrededor del eje vertical O1Z1 de un sistema de referencia fijo O1X1Y1Z1 (sólido "1"). Determina las magnitudes cinemáticas  y
y  en el instante representado en la figura.
en el instante representado en la figura.
1.4 Disco y varilla con dos rotaciones
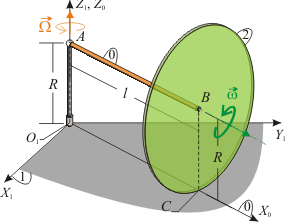
El sistema de la figura está formado por una varilla AB de longitud l (sólido "0"), cuyo extremo A está fijado en el eje vertical O1Z1, a una altura R sobre el plano horizontal fijo O1X1Y1 (sólido "1"). La varilla AB gira alrededor de O1Z1 con una velocidad angular constante Ω, permaneciendo siempre perpendicular a dicho eje vertical fijo. El extremo B del sólido "0" está articulado al centro de un disco de radio R (sólido "2"), de modo que la varilla es siempre perpendicular al disco. El disco gira con una velocidad angular constante ω, coincidiendo su eje de giro con la varilla.
- Caracterice los movimientos {01}, {20} y {21} (reducciones cinemáticas).
- Obtenga la expresión de la velocidad
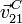 del punto de contacto del disco con el plano fijo O1X1Y1, (punto C) en términos de los datos del problema. ¿Qué relación debe existir entre las velocidades angulares ω y Ω para que el disco ruede sin deslizar sobre el plano?
del punto de contacto del disco con el plano fijo O1X1Y1, (punto C) en términos de los datos del problema. ¿Qué relación debe existir entre las velocidades angulares ω y Ω para que el disco ruede sin deslizar sobre el plano?
- Obtenga las expresiones de la aceleración angular del movimiento {21} y de la aceleración
 del centro del disco (punto B). Calcule la aceleración del punto de contacto C perteneciente al disco cuando éste rueda sin deslizar sobre el plano O1X1Y1.
del centro del disco (punto B). Calcule la aceleración del punto de contacto C perteneciente al disco cuando éste rueda sin deslizar sobre el plano O1X1Y1.
1.5 Cono rodando sin deslizar sobre plano
Un cono recto de radio R en su base y una altura
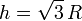 (sólido “2”), se mueve rodando sin deslizar sobre el plano fijo O1X1Y1 (sólido “1”), en el cuál apoya, en cada instante, una generatriz
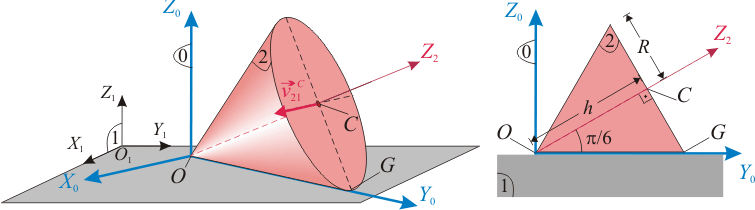
(sólido “2”), se mueve rodando sin deslizar sobre el plano fijo O1X1Y1 (sólido “1”), en el cuál apoya, en cada instante, una generatriz 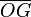 . La velocidad del centro C de la base del cono, medida desde el sistema de referencia ligado al sólido “1”, tiene módulo constante de valor v0. Para facilitar la descripción del movimiento, se introduce un sistema de referencia OX0Y0Z0 (sólido “0”) con origen O en el vértice del cono, el eje OZ0 siempre perpendicular al plano fijo “1”, y cuyo eje OY0 contiene en cada instante a la generatriz del cono en contacto con dicho plano.
. La velocidad del centro C de la base del cono, medida desde el sistema de referencia ligado al sólido “1”, tiene módulo constante de valor v0. Para facilitar la descripción del movimiento, se introduce un sistema de referencia OX0Y0Z0 (sólido “0”) con origen O en el vértice del cono, el eje OZ0 siempre perpendicular al plano fijo “1”, y cuyo eje OY0 contiene en cada instante a la generatriz del cono en contacto con dicho plano.
- Reducciones cinematicas de los movimientos relativos.
- Ejes de rotación y naturaleza de los movimientos.
- Campos de aceleraciones.
1.6 Enunciado
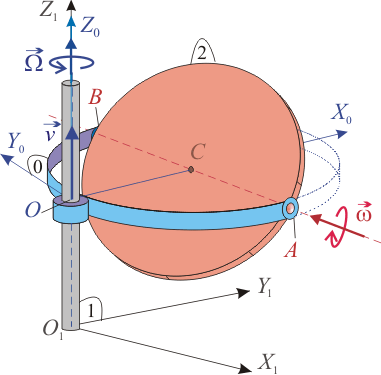
El sistema de la figura consiste en una horquilla semicircular (sólido "0"), que siempre está paralela al plano fijo O1X1Y1 (sólido "1"). El punto O de dicho aro (siempre el mismo) se desplaza con velocidad v sobre el eje O1Z1, a la vez que el aro gira con velocidad angular constante Ω alrededor de dicho eje fijo. Un disco de radio R (sólido "2"), se mueve respecto a "0" girando alrededor del diámetro común AB, con velocidad angular constante ω.
Nota: Los valores de Ω, ω y v pueden ser positivos o negativos.
- ¿Cuándo es nula la velocidad mínima del movimiento {21}?
- Qué debe ocurrir para que el eje instantáneo de rotación y mínimo deslizamiento pase por el centro del disco? Calcule en este caso la derivada temporal de la reducción cinemática
- ¿Qué condición debe cumplirse para que el movimiento {21} sea una rotación instantánea y el eje instantáneo de rotación pase por el centro del disco?