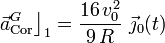Ejercicio de cinemática del sólido rígido y movimiento relativo, Enero 2012
De Laplace
Contenido |
1 Enunciado
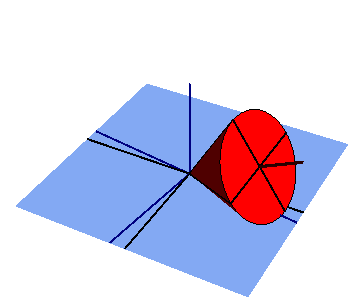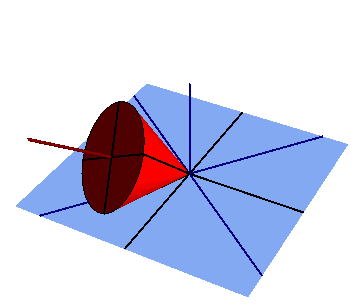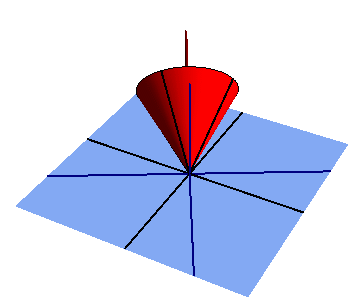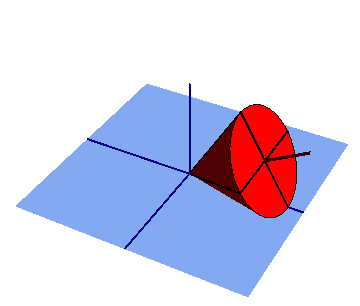
Un cono recto de radio R en su base y una altura
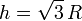 (sólido “2”), se mueve rodando sin deslizar sobre el plano fijo O1X1Y1 (sólido “1”), en el cuál apoya, en cada instante, una generatriz
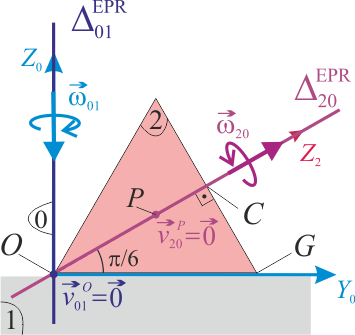
(sólido “2”), se mueve rodando sin deslizar sobre el plano fijo O1X1Y1 (sólido “1”), en el cuál apoya, en cada instante, una generatriz 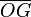 . La velocidad del centro C de la base del cono, medida desde el sistema de referencia ligado al sólido “1”, tiene módulo constante de valor v0. Para facilitar la descripción del movimiento, se introduce un sistema de referencia OX0Y0Z0 (sólido “0”) con origen O en el vértice del cono, el eje OZ0 siempre perpendicular al plano fijo “1”, y cuyo eje OY0 contiene en cada instante a la generatriz del cono en contacto con dicho plano.
. La velocidad del centro C de la base del cono, medida desde el sistema de referencia ligado al sólido “1”, tiene módulo constante de valor v0. Para facilitar la descripción del movimiento, se introduce un sistema de referencia OX0Y0Z0 (sólido “0”) con origen O en el vértice del cono, el eje OZ0 siempre perpendicular al plano fijo “1”, y cuyo eje OY0 contiene en cada instante a la generatriz del cono en contacto con dicho plano.
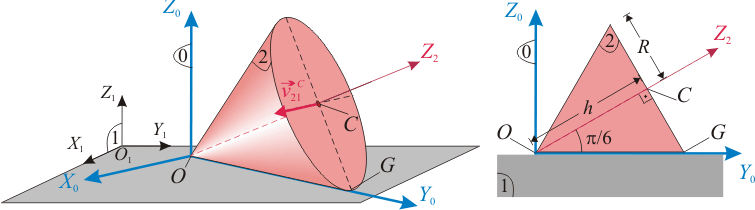
- Reducciones cinematicas de los movimientos relativos.
- Ejes de rotación y naturaleza de los movimientos.
- Campos de aceleraciones.
2 Solución
2.1 Reducciones cinemáticas
2.1.1 Análisis del movimiento {21}
Con los datos que nos proporciona el enunciado, la reducción cinematica instantánea más fácil de determinar corresponde al movimiento del cono (sólido “2”), respecto del plano fijo (sólido “1”). Como el primero rueda sin deslizar sobre el segundo, los puntos del cono que se encuentran en la generatriz 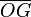 donde se produce el contacto instantáneo se encuentran en reposo:
donde se produce el contacto instantáneo se encuentran en reposo:
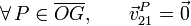
Nos indican que, en dicho movimiento {21}, el centro C de la base del cono se desplaza con velocidad constante de valor v0. Por tanto, en cada instante este movimiento es una rotación pura en la que los puntos de la generatriz de contacto con el plano fijo, 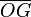 , deben ser puntos del eje de rotación. Obsérvese que dicha generatriz irá cambiando durante el movimiento, por lo que los puntos del cono con velocidad nula no van a ser siempre los mismos. O lo que es lo mismo, si P es un punto del cono en contacto con el plano fijo en un cierto instante, su velocidad es nula en ese instante, pero no en el inmediatamente posterior; es decir, su aceleración va a ser no nula y, en consecuencia, el eje de la rotación {21} tendrá carácter instantáneo:
, deben ser puntos del eje de rotación. Obsérvese que dicha generatriz irá cambiando durante el movimiento, por lo que los puntos del cono con velocidad nula no van a ser siempre los mismos. O lo que es lo mismo, si P es un punto del cono en contacto con el plano fijo en un cierto instante, su velocidad es nula en ese instante, pero no en el inmediatamente posterior; es decir, su aceleración va a ser no nula y, en consecuencia, el eje de la rotación {21} tendrá carácter instantáneo:
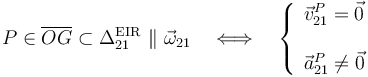
Sin embargo ha de hacerse una excepción con el vértice O del cono: como este punto es la intersección de todas sus generatrices, en todo momento se encuentra en contacto con el plano fijo, sin deslizar sobre él; es decir, el vértice O del cono está en reposo permanente respecto del sólido “1”:
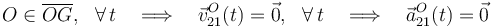
Determinemos ahora el valor instantáneo del vector rotación  que caracteriza a este movimiento. Por simplicidad, lo expresaremos en el sistema de referencia OX0Y0Z0 (sólido “0”) propuesto en el enunciado que, en cada instante, tiene el eje OY0 alineado con la generatriz de contacto y, por tanto, con
que caracteriza a este movimiento. Por simplicidad, lo expresaremos en el sistema de referencia OX0Y0Z0 (sólido “0”) propuesto en el enunciado que, en cada instante, tiene el eje OY0 alineado con la generatriz de contacto y, por tanto, con  . El valor instantáneo de la componente estará directametne relacionado con el módulo de la velocidad del punto C, de valor constante conocido, v0:
. El valor instantáneo de la componente estará directametne relacionado con el módulo de la velocidad del punto C, de valor constante conocido, v0:
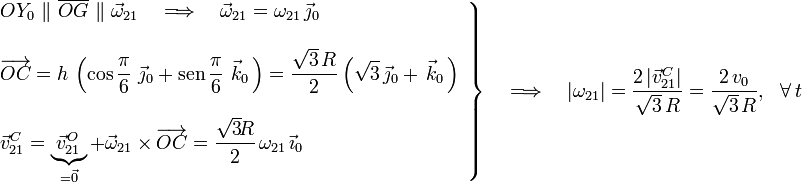
El signo de ω21 y, por tanto, el sentido de la rotación instantánea  , no están determinados a priori por ninguno de los datos proporcionados en el enunciado, por lo que podremos tomar cualquiera de los dos posibles. En la figura se indica, a modo de ilustración, un sentido concreto para la velocidad del centro C de la base del cono. Dicho sentido de movimiento se correspondería con una rotación isntantánea antihoraria del cono alrededor del eje
, no están determinados a priori por ninguno de los datos proporcionados en el enunciado, por lo que podremos tomar cualquiera de los dos posibles. En la figura se indica, a modo de ilustración, un sentido concreto para la velocidad del centro C de la base del cono. Dicho sentido de movimiento se correspondería con una rotación isntantánea antihoraria del cono alrededor del eje 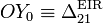 . Para esta situación, la reducción cinemática canónica que caracteriza el movimiento instantáneo del cono respecto del plano fijo, es:
. Para esta situación, la reducción cinemática canónica que caracteriza el movimiento instantáneo del cono respecto del plano fijo, es:
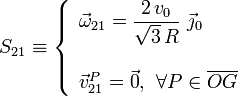
Con esta reducción podemos determinar el campo de velocidades correspondiente al movimiento del sólido “2” respecto del “1” en un determinado instante, y que también podría ser obtenido con una reducción no canónica, por ejemplo...
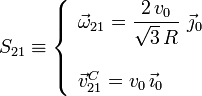
Sin embargo, con los datos del enunciado podemos obtener la expresión de una reducción -canónica, además- como una función del tiempo que nos permitiría calcular el campo de velocidades en cualquier instante. Anterioremente determinamos que el vértice del cono está en reposo permanente respecto del plano fijo y, por tanto, ocupa un punto fijo O de dicho plano. Además, como el cono rueda siempre sin deslizar, la dirección del vector rotación es paralela en cada instante a la de la generatriz de contacto, o lo que es lo mismo, a la dirección dada por el unitario 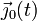 del sólido “0”. Y como el módulo de la velocidad del centro C es constante, también lo será la componente del vector
del sólido “0”. Y como el módulo de la velocidad del centro C es constante, también lo será la componente del vector 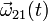 :
:
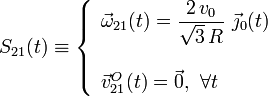
Realmente, para tener completamente descrita el movimiento {21} en todo instante, debemos indicar cómo cambia en el tiempo el vector unitario 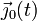 . Esto lo haremos mediante la reducción cinemática del movimiento {01}, que calcularemos en el siguiente apartado junto con la del {20}.
. Esto lo haremos mediante la reducción cinemática del movimiento {01}, que calcularemos en el siguiente apartado junto con la del {20}.
2.1.2 Descripción de los movimientos {20} y {01}
El sistema de referencia “0” ha sido definido de manera que, en todo instante, su origen O coincide con el vértice del cono. Por tanto, éste es un punto en reposo permanente respecto en el movimiento {20}:
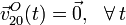
Por otra parte, en el apartado anterior vimos que el segmento orientado  se puede expresar como una combinación lineal de los vectores unitarios
se puede expresar como una combinación lineal de los vectores unitarios 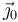 y
y  , que no va a cambiar en el tiempo, pues
, que no va a cambiar en el tiempo, pues  formará en todo instante un ángulo de π / 6 con el eje OY0. En consecuencia, el centro C de la base del cono se encuentra en reposo permanente en el plano OY0Z0:
formará en todo instante un ángulo de π / 6 con el eje OY0. En consecuencia, el centro C de la base del cono se encuentra en reposo permanente en el plano OY0Z0:
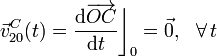
Este mismo resultado puede extenderse a cualquiera de los puntos del eje 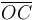 de manera que, en el movimiento relativo del cono (sólido “2”) respecto del sistema de referencia OX0Y0Z0 (sólido “0”), todos ellos se encuentran en reposo permanente. Sin embargo, hay puntos del cono que tienen velocidadades
no nulas en el movimiento {20}. Por ejemplo, los que constituyen la generatriz de contacto
de manera que, en el movimiento relativo del cono (sólido “2”) respecto del sistema de referencia OX0Y0Z0 (sólido “0”), todos ellos se encuentran en reposo permanente. Sin embargo, hay puntos del cono que tienen velocidadades
no nulas en el movimiento {20}. Por ejemplo, los que constituyen la generatriz de contacto 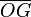 y se encuentran en el eje OY0, que van a ir cambiando en el transcurso del tiempo. En consecuencia, dicho movimiento es una rotación pura permanente cuyo eje coincide con el eje de simetría del cono, quedando así determinada la dirección del vector rotación insantánea
y se encuentran en el eje OY0, que van a ir cambiando en el transcurso del tiempo. En consecuencia, dicho movimiento es una rotación pura permanente cuyo eje coincide con el eje de simetría del cono, quedando así determinada la dirección del vector rotación insantánea  :
:
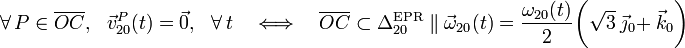
En cuanto al movimiento {01}, sabemos que el vértice del cono y origen del sistema de referencia “0” (punto O), se encuentra en reposo permanente en el plano O1X1Y1, de manera que,
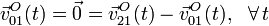
Como las rotaciones instantáneas  y
y  son distintas al tener direcciones diferentes, el vector rotación
son distintas al tener direcciones diferentes, el vector rotación  ha de ser forzosamente no nulo. En consecuencia, el movimiento {01} será también, en todo instante de tiempo, una rotación pura. La dirección del vector
ha de ser forzosamente no nulo. En consecuencia, el movimiento {01} será también, en todo instante de tiempo, una rotación pura. La dirección del vector  y, por tanto, del eje de rotación, están determinadas por la elección del eje OZ0 siempre perpendicular al plano fijo O1X1Z1: en virtud de las fórmulas de Poisson, se tendrá que,
y, por tanto, del eje de rotación, están determinadas por la elección del eje OZ0 siempre perpendicular al plano fijo O1X1Z1: en virtud de las fórmulas de Poisson, se tendrá que,
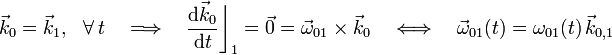
Aplicando ahora la ley de composición de los vectores rotación instantánea para movimientos relativos, se obtiene sendas ecuaciones,
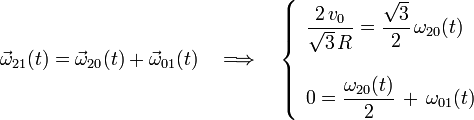
que permiten determinar los valores de las componentes ω20 y ω01, en cualquier instante de tiempo. Y con éstas quedan completamente determinadas las reducciones cinemáticas de los movimientos {20} y {01}:
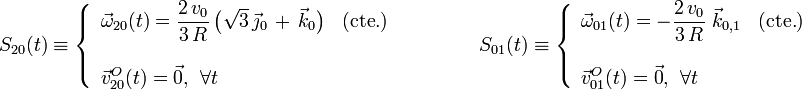
2.2 Ejes de rotación y tipos de movimientos
Las discusiones realizadas en el apartado anterior para obtener las reducciones cinemáticas Sij(t), nos permitieron identificar los tipos de movimiento relativo que realizan cada par de sólidos del sistema. Allí encontramos que, en todo instante, cada sólido efectúa una rotación pura respecto de cualquiera de los otros.
Tal como se discutió anteriormente (y acabamos de describir en S20(t)) los puntos del eje 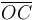 están en reposo permanente respecto del sólido “0”, mientras que el resto del cono efectúa una rotación alrededor de dicho eje, cuya dirección es constante en aquél sistema de referencia. Así, el movimiento {20} es una rotación permanente cuyo eje permanente de rotación es:
están en reposo permanente respecto del sólido “0”, mientras que el resto del cono efectúa una rotación alrededor de dicho eje, cuya dirección es constante en aquél sistema de referencia. Así, el movimiento {20} es una rotación permanente cuyo eje permanente de rotación es:
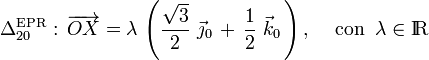
Obsérvese que el movimiento {01} es complemente análogo: hemos justificado que el vertice del cono y, por tanto, el origen O del sólido “0” está en reposo permanente en el plano O1X1Y1 del sólido “1”; además,  y el correspondiente eje de rotación tiene dirección constante: la indicada por los unitarios
y el correspondiente eje de rotación tiene dirección constante: la indicada por los unitarios 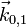 . En consecuencia, este movimiento es una rotación permanente alrededor del eje,
. En consecuencia, este movimiento es una rotación permanente alrededor del eje,
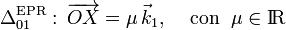
En cuanto al movimiento {21}, al principio del apartado 2.1.1 determinamos que se trataba de una rotación pura con carácter instantáneo, lo cuál es corroborado por la reducción S21(t): existe un punto del cono (su vértice O), que se encuentra en reposo permanente. Sin embargo, la dirección del vector rotación  y, por tanto, del eje de rotación, cambian en el tiempo, coincidiendo en cada instante con la del eje OY0. La ecuación vectorial del correspondiente eje de rotación es:
y, por tanto, del eje de rotación, cambian en el tiempo, coincidiendo en cada instante con la del eje OY0. La ecuación vectorial del correspondiente eje de rotación es:
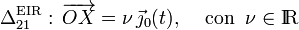
2.3 Campos de aceleraciones
El campo de aceleraciones instantáneas del sólido rígido “i” en movimiento relativo respecto del “j” verifica la ley general
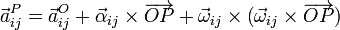
donde P y O son dos puntos cualesquiera del sólido “i”. Si este último es el centro de reducción, tenemos que el campo de aceleraciones quedará completamente determinado por el vector rotación instantánea y (los valores de) las derivadas temporales de la reducción cinemática Sij(t).
En el apartado anterior hemos obtenido las expresiones temporales de las reducciones cinematicas correspondientes a los tres movimientos relativos del sistema. Además, para los tres hemos utilizado el mismo centro de reducción: el vértice O del cono, que se halla en reposo permanente en cualquiera de los movimiento y que, por tanto, también tendrá aceleración nula.
Así, para el movimiento {20} tendremos:
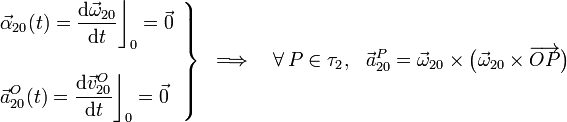
Estas expresiones nos indican que la aceleración instantánea de cada punto en el movimiento {20} es la correspondiente a un movimiento circular uniforme alrededor del eje permanente 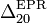 .
.
Para el movimiento {01} obtenemos un resultado similar, por tratarse también de un movimiento de rotación permanente con vector rotación de módulo constante:
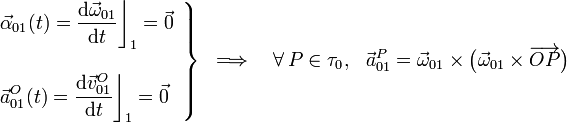
Y para el movimiento {21}, por tratarse de una rotación instantánea, se tendrá:
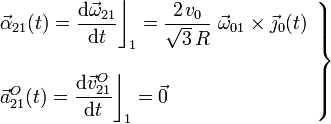



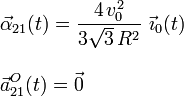



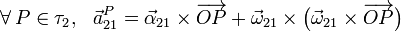
2.3.1 Aceleración de Coriolis del punto G
La ley de composición de aceleraciones instantáneas establece que,
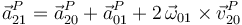
para todo punto P del espacio, y donde el tercer término del segundo miembro es la aceleración de Coriolis para dicho punto. Por tanto, si queremos calcular el término de Coriolis para la aceleración absoluta del punto G del cono podemos, bien realizar el cálculo directo, bien obtenerla como la diferencia entre la aceleración absoluta de dicho punto, y las aceleraciones relativa y de arrastre:
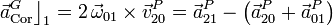
Con cualquiera de ambos procedimientos se obtiene idéntico resultado: