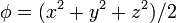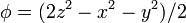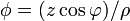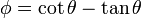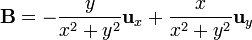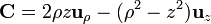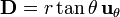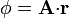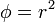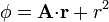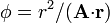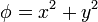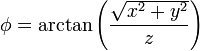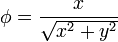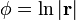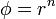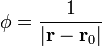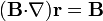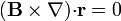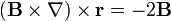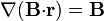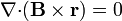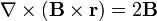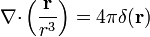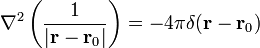Entrar Página Discusión Historial Go to the site toolbox

Problemas de fundamentos matemáticos

De Laplace

(Diferencias entre revisiones)
Línea 113: Línea 113:
Se define la ''función'' delta de Dirac en tres dimensiones como aquella distribución que verifica
Se define la ''función'' delta de Dirac en tres dimensiones como aquella distribución que verifica
-
<center><math>\delta(\mathbf{r})=0</math>{{qquad}}<math>(\mathbf{r}\neq 0)</math></center>
+
<center><math>\delta(\mathbf{r})=0</math>{{qquad}}<math>(\mathbf{r}\neq 0)</math>{{qquad}}{{qquad}}<math>\int \delta(\mathbf{r})\,\mathrm{d}\tau=1</math></center>
-
 
+
-
<center><math>\int \delta(\mathbf{r})\,\mathrm{d}\tau=1</math></center>
+
con la última integral extendida a todo el espacio.
con la última integral extendida a todo el espacio.
Línea 123: Línea 121:
# <math>\nabla{\cdot}\left(\displaystyle\frac{\mathbf{r}}{r^3}\right)=4\pi\delta(\mathbf{r})</math>
# <math>\nabla{\cdot}\left(\displaystyle\frac{\mathbf{r}}{r^3}\right)=4\pi\delta(\mathbf{r})</math>
# <math>\nabla^2\left(\displaystyle\frac{1}{|\mathbf{r}-\mathbf{r}_0|}\right)= -4\pi\delta(\mathbf{r}-\mathbf{r}_0)</math>
# <math>\nabla^2\left(\displaystyle\frac{1}{|\mathbf{r}-\mathbf{r}_0|}\right)= -4\pi\delta(\mathbf{r}-\mathbf{r}_0)</math>
 +
 +
==[[Cálculo de laplacianos]]==
 +
Calcule el laplaciano de los campos escalares
 +
 +
# <math>\phi = (x^2+y^2+z^2)/2</math>
 +
# <math>\phi = (2z^2-x^2-y^2)/2</math>
 +
# <math>\phi = \rho^3\cos\varphi</math>
 +
# <math>\phi = r^3\,\mathop{sen}\theta</math>
 +
 +
empleando coordenadas cartesianas, cilíndricas y esféricas.
[[Categoría:Problemas de fundamentos matemáticos]]
[[Categoría:Problemas de fundamentos matemáticos]]

Revisión de 09:07 23 sep 2008

Contenido

1 Campos escalares en diferentes sistemas

Exprese los siguientes campos escalares en coordenadas cartesianas, cilíndricas y esféricas

  1. \phi = (x^2+y^2+z^2)/2\,
  2. \phi = (2z^2-x^2-y^2)/2\,
  3. \phi = (z\cos\varphi)/\rho
  4. \phi = \cot\theta - \tan\theta\,

2 Campos vectoriales en diferentes sistemas

Exprese los siguientes campos vectoriales en coordenadas cartesianas, cilíndricas y esféricas:

  1. \mathbf{A} = \mathbf{r}\,
  2. \mathbf{B} = -\dfrac{y}{x^2+y^2}\mathbf{u}_{x}+\dfrac{x}{x^2+y^2}\mathbf{u}_{y}
  3. \mathbf{C} = 2\rho z\mathbf{u}_{\rho}-(\rho^2-z^2)\mathbf{u}_{z}
  4. \mathbf{D}=r\tan\theta\,\mathbf{u}_{\theta}

3 Trazado de superficies equiescalares

Describa las superficies equipotenciales de los siguientes campos escalares

  1. \phi=\mathbf{A}{\cdot}\mathbf{r}\,
  2. \phi=r^2\,
  3. \phi=\mathbf{A}{\cdot}\mathbf{r}+r^2\,
  4. \phi= r^2/(\mathbf{A}{\cdot}\mathbf{r})
  5. \phi = x^2 + y^2\,
  6. \phi = \arctan\left(\displaystyle\frac{\sqrt{x^2+y^2}}{z}\right)
  7. \phi= \frac{x}{\sqrt{x^2+y^2}}

donde \mathbf{A} es un vector constante y \mathbf{r} es el vector de posición.

4 Cálculo de gradientes

Para los campos escalares

  1. \phi = (x^2+y^2+z^2)/2\,
  2. \phi = (2z^2-x^2-y^2)/2\,

calcule su gradiente en coordenadas cartesianas, cilíndricas y esféricas.

5 Regla de la cadena para gradientes

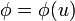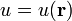Si \phi = \phi(u)\,, con u = u(\mathbf{r}), demuestre que

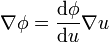
\nabla \phi = \frac{\mathrm{d}\phi}{\mathrm{d}u} \nabla u

Encuentre 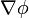\nabla \phi si

  1. \phi=\ln|\mathbf{r}|\,
  2. \phi =r^n\,
  3. \phi=\frac{1}{|\mathbf{r} -\mathbf{r}_0|}

6 Integral sobre una superficie esférica

Halle el valor de la integral

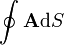
\oint \mathbf{A} \mathrm{d}S

con

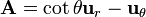
\mathbf{A}=\cot\theta\mathbf{u}_{r}-\mathbf{u}_{\theta}

y la superficie de integración una esfera de radio R centrada en el origen.

7 Cálculo de divergencias y rotacionales

Para los campos vectoriales

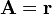
  1. \mathbf{A} = \mathbf{r}\,
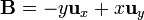
  2. \mathbf{B}=-y\mathbf{u}_{x}+x\mathbf{u}_{y}\,
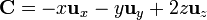
  3. \mathbf{C} = -x\mathbf{u}_{x}-y\mathbf{u}_{y}+2z\mathbf{u}_{z}\,
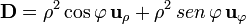  4. \mathbf{D} = \rho^2\cos\varphi\,\mathbf{u}_{\rho}+\rho^2\,\mathop{sen}\,\varphi\,\mathbf{u}_{\varphi}$

calcule su divergencia y su rotacional, empleando en cada caso, coordenadas cartesianas, cilíndricas y esféricas. ¿Cuáles son irrotacionales y cuáles solenoidales?

8 Cálculo de flujo

Para el campo vectorial

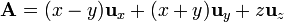
\mathbf{A} = (x-y)\mathbf{u}_{x}+(x+y)\mathbf{u}_{y}+z\mathbf{u}_{z}\,

calcule su flujo a través de las siguientes superficies cerradas:

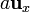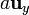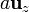  1. Un cubo de arista a, con un vértice en el origen y aristas a\mathbf{u}_{x}, a\mathbf{u}_{y} y a\mathbf{u}_{z}.
  2. Un cilindro circular de altura h y radio R, con el eje Z como eje y sus bases situadas en z = 0 y z = h.
  3. Una esfera de radio R en torno al origen de coordenadas.

En cada caso, halle el flujo por integración directa y por aplicación del teorema de Gauss.

9 Cálculo de circulación

Para el campo vectorial

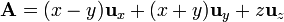
\mathbf{A} = (x-y)\mathbf{u}_{x}+(x+y)\mathbf{u}_{y}+z\mathbf{u}_{z}

calcule su circulación a lo largo de las siguientes curvas cerradas:

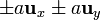  1. Un cuadrado de lado 2a, con vértices \pm a\mathbf{u}_{x}\pm a\mathbf{u}_{y}.
  2. Una circunferencia de radio R situada en el plano z = 0 y con centro el origen de coordenadas.
  3. Una circunferencia vertical, situada en el plano x = y y con centro el origen de coordenadas.

En cada caso, halle la circulación por integración directa y por aplicación del teorema de Stokes.

10 Demostración de identidades vectoriales

Demuestre que si \mathbf{r} es el vector de posición y \mathbf{B} un campo vectorial arbitrario

  1. (\mathbf{B}{\cdot}\nabla)\mathbf{r}=\mathbf{B}
  2. (\mathbf{B}\times\nabla){\cdot}\mathbf{r}=0
  3. (\mathbf{B}\times\nabla)\times\mathbf{r}=-2\mathbf{B}

Igualmente, para el caso particular en que $\mathbf{B}$ represente un vector constante, demuestre que

  1. \nabla(\mathbf{B}{\cdot}\mathbf{r})=\mathbf{B}
  2. \nabla{\cdot}(\mathbf{B}\times\mathbf{r})=0
  3. \nabla\times(\mathbf{B}\times\mathbf{r})=2\mathbf{B}

11 Propiedades de la Delta de Dirac

Se define la función delta de Dirac en tres dimensiones como aquella distribución que verifica

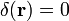
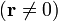
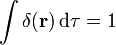
\delta(\mathbf{r})=0    (\mathbf{r}\neq 0)        \int \delta(\mathbf{r})\,\mathrm{d}\tau=1

con la última integral extendida a todo el espacio.

Pruebe que:

  1. \nabla{\cdot}\left(\displaystyle\frac{\mathbf{r}}{r^3}\right)=4\pi\delta(\mathbf{r})
  2. \nabla^2\left(\displaystyle\frac{1}{|\mathbf{r}-\mathbf{r}_0|}\right)= -4\pi\delta(\mathbf{r}-\mathbf{r}_0)

12 Cálculo de laplacianos

Calcule el laplaciano de los campos escalares

  1. φ = (x2 + y2 + z2) / 2
  2. φ = (2z2 − x2 − y2) / 2
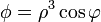
  3. \phi = \rho^3\cos\varphi
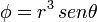
  4. \phi = r^3\,\mathop{sen}\theta

empleando coordenadas cartesianas, cilíndricas y esféricas.

Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_fundamentos_matem%C3%A1ticos"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace