Movimiento ondulatorio
De Laplace
(→Ondas longitudinales) |
(→Problemas) |
||
| (30 ediciones intermedias no se muestran.) | |||
| Línea 2: | Línea 2: | ||
==Ondas transversales y longitudinales== | ==Ondas transversales y longitudinales== | ||
===Ondas longitudinales=== | ===Ondas longitudinales=== | ||
| - | + | En una onda longitudinal la vibración de las partículas se produce en la misma dirección en que se propaga la onda. | |
| - | + | ||
| + | El caso más común de onda longitudinal es el de las ondas de compresión, en el que las partículas vibran en un sentido, tradmitiendo su vibración a las partículas adyacentes. A este tipo de ondas de compresión pertenece el '''sonido''' (en particular, para el caso de que el medio material sea el aire), y las ondas sísmicas P. | ||
| + | |||
====Onda sinusoidal==== | ====Onda sinusoidal==== | ||
| + | Cuando tenemos una oscilación periódica, cada partícula oscila en torno a su posición de equilibrio con una variación de la forma | ||
| + | |||
| + | <center><math>x_i(t) = x_{i\mathrm{eq}} + s_0 \cos(\omega t - k x + \phi)\,</math></center> | ||
| + | |||
| + | Aunque la onda avanza, observando cada una de las partículas individualmente, puede verse que en promedio cada una permanece inmóvil. | ||
| + | |||
<center>[[Imagen:Ondalongitudinal.gif]]</center> | <center>[[Imagen:Ondalongitudinal.gif]]</center> | ||
| - | |||
====Pulso==== | ====Pulso==== | ||
| - | <center>[[Imagen: | + | Una onda (longitudinal o transversal) no tiene por qué ser necesariamente una sinusoide. Un golpe seco en un extremo de un material produce un ''pulso'', que se mueve a lo largo de él. Este pulso es también una onda. |
| + | |||
| + | <center>[[Imagen:Pulsolongitudinal.gif]]</center> | ||
| + | |||
| + | ===Ondas transversales=== | ||
| + | En una onda transversal cada partícula se mueve perpendicularmente a la dirección en que avanza la onda, de forma que para una onda sinusoidal sería | ||
| + | |||
| + | <center><math>y = A \cos(\omega t - k x)\,</math></center> | ||
| + | |||
| + | Más en general, una onda transversal es una combinación de una señal que se propaga en un sentido más una que se propaga en el sentido opuesto, lo cual se puede escribir en la forma general | ||
| + | |||
| + | <center><math>y = f\left(x-vt\right)+g(x+vt)\,</math></center> | ||
| + | |||
| + | siendo <math>f</math> y <math>g</math> funciones arbitrarias de una variable (aunque si representan ondas físicas reales, además son acotadas). | ||
====Onda sinusoidal==== | ====Onda sinusoidal==== | ||
<center>[[Imagen:Ondatransversal.gif]]</center> | <center>[[Imagen:Ondatransversal.gif]]</center> | ||
| + | |||
| + | ====Pulso==== | ||
| + | <center>[[Imagen:Pulsotransversal.gif]]</center> | ||
===Combinaciones de ondas=== | ===Combinaciones de ondas=== | ||
| + | Una onda puede ser una combinación de una onda longitudinal y una transversal, de forma que cada partícula describe un movimiento elíptico. | ||
| + | |||
| + | En particular, la trayectoria individual puede ser una circunferencia, esto es lo que ocurre para las ondas superficiales en agua (qque no son transversales, como suele suponerse), el movimiento de cada partícula es | ||
| + | |||
| + | <center><math>x = x_\mathrm{eq} + A\cos(\omega t - k x_\mathrm{eq})\,</math>{{qquad}}{{qquad}} <math>y = A\,\mathrm{sen}\,(\omega t - kx_\mathrm{eq})\,</math></center> | ||
| + | |||
| + | |||
<center>[[Imagen:Ondacircular.gif]]</center> | <center>[[Imagen:Ondacircular.gif]]</center> | ||
| - | == | + | ==Ecuación de onda== |
| - | === | + | Una onda puede definirse, de forma matemática, como una solución de la ''ecuación de onda'', que es una ecuación diferencial concreta. |
| - | ===Deducción de la ecuación de onda en una dimensión=== | + | |
| + | Si el análisis de una magnitud de un sistema físico conduce a una ecuación diferencial de la misma forma que la ecuación de onda, se puede concluir que la solución para dicha magnitud es un comportamiento ondulatorio, aunque no se trate de un sistema mecánico y no haya verdadero movimiento de partículas (esto es lo que ocurre, por ejemplo, con las ondas electromagnéticas). | ||
| + | |||
| + | ===En una dimensión=== | ||
| + | Si tenemos una magnitud <math>u</math> que depende de una coordenada <math>x</math> y del tiempo, esta magnitud presenta comportamiento ondulatorio si se satisface la ecuación diferencial en derivadas parciales | ||
| + | |||
| + | <center><math>\frac{\partial^2u}{\partial x^2}-\frac{1}{v^2}\frac{\partial^2 u}{\partial t^2}=0</math></center> | ||
| + | |||
| + | siendo <math>v</math> la velocidad de la onda. | ||
| + | |||
| + | ;Ondas en una cuerda tensa | ||
| + | :Por ejemplo, en el caso de una cuerda tensa puede demostrarse que los movimientos transversales verifican la ecuación | ||
| + | |||
| + | <center><math>\mu\frac{\partial^2y}{\partial t^2} = F_T\frac{\partial^2y}{\partial x^2}</math></center> | ||
| + | |||
| + | :siendo <math>\mu</math> la densidad lineal de masa y <math>F_T</math> la tensión de la cuerda. Reescribiendo esta ecuación como | ||
| + | |||
| + | <center><math>\frac{\partial^2y}{\partial x^2}-\frac{1}{F_T/\mu}\frac{\partial^2y}{\partial t^2} = 0</math></center> | ||
| + | |||
| + | :vemos que el movimiento de la cuerda tensa es ondulatorio, siendo su velocidad | ||
| + | |||
| + | <center><math>v = \sqrt{\frac{F_T}{\mu}}</math></center> | ||
| + | |||
| + | ;Ondas electromagnéticas:Al analizar el comportamiento de los campos eléctricos y magnéticos dependientes del tiempo, Maxwell llegó a la conclusión de que en el espacio vacío un campo eléctrico dependiente de una sola coordenada verifica la ecuación | ||
| + | |||
| + | <center><math>\frac{\partial^2\mathbf{E}}{\partial x^2}-\mu_0\varepsilon_0\frac{\partial^2\mathbf{E}}{\partial t^2}=\mathbf{0}</math></center> | ||
| + | |||
| + | :siendo <math>\varepsilon_0</math> y <math>\mu_0</math> dos constantes físicas denominadas permitividad y permeabilidad del vacío: | ||
| + | |||
| + | <center><math>\varepsilon_0\simeq \frac{1}{36\pi\times 10^{9}}\,\frac{\mathrm{F}}{\mathrm{m}}</math>{{qquad}}{{qquad}}<math>\mu_0= 4\pi\times 10^{-7}\,\frac{\mathrm{H}}{\mathrm{m}}</math></center> | ||
| + | |||
| + | :De esta ecuación resulta que el campo eléctrico (y el magnético) tiene un comportamiento ondulatorio, siendo su velocidad | ||
| + | |||
| + | <center><math>c = \frac{1}{\sqrt{\varepsilon_0\mu_0}}\simeq 3\times 10^8\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | :que es exactamente la velocidad de la luz. De esto Maxwell concluyó que la luz es una onda electromagnético. | ||
| + | ====Principio de superposición==== | ||
| + | Una propiedad importante de la ecuación de onda es que es ''lineal'', esto es, que verifica el ''principio de superposición'': si <math>u_1</math> y <math>u_2</math> son dos soluciones, cualquier superposición | ||
| + | |||
| + | <center><math>u=a u_1 + bu_2\,</math></center> | ||
| + | |||
| + | con <math>a</math> y <math>b</math> constantes es también una solución. | ||
| + | |||
| + | ====Solución general de la ecuación de onda==== | ||
| + | Puede demostrarse que la solución general de la ecuación de onda | ||
| + | |||
| + | <center><math>\frac{\partial^2u}{\partial x^2}-\frac{1}{v^2}\frac{\partial^2 u}{\partial t^2}=0</math></center> | ||
| + | |||
| + | es una función de la forma | ||
| + | |||
| + | <center><math> u = f(x-vt) + g(x+vt)\,</math></center> | ||
| + | |||
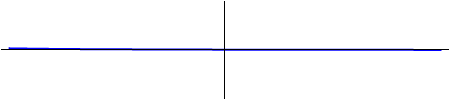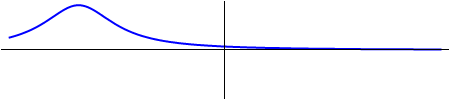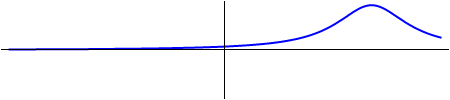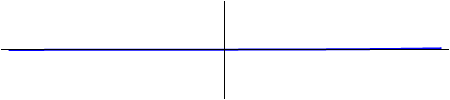
| + | siendo <math>f</math> y <math>g</math> dos funciones cualesquiera de una variable. No obstante, para una onda real de un sistema físico no pueden ser cualesquiera, sino que deben ser continua, derivable y acotada (no irse a infinito). Aun así, esto dejea mucha libertad a las soluciones: pulsos, ondas viajeras y estacionarias son soluciones de la ecuación de onda. | ||
| + | |||
| + | [[Imagen:onda_viajera_derecha.gif|right]] | ||
| + | |||
| + | En particular, si <math>g=0</math> nos queda la solución | ||
| + | |||
| + | <center><math>u = f(x-vt)\,</math></center> | ||
| + | |||
| + | que es una ''onda viajera'' que se propaga hacia <math>x</math> creciente. Esta onda conserva su forma (ya que <math>f(s)</math> es siempre la misma, solo va cambiando su posición) | ||
| + | |||
| + | [[Imagen:onda_viajera_izquierda.gif|right]] | ||
| + | |||
| + | Si <math>f=0</math>, la solución es de la forma | ||
| + | |||
| + | <center><math>u = g(x+vt)\,</math></center> | ||
| + | |||
| + | que es una ''onda viajera'' propagándose hacia los valores de <math>x</math> decrecientes | ||
| + | |||
| + | [[Imagen:onda_viajera_suma.gif|right]] | ||
| + | |||
| + | En el caso general, la solución es una superposición de una señal que se propaga hacia la derecha con una que se propaga hacia la izquierda. Así, por ejemplo, una [[onda estacionaria]] puede verse como la suma de dos sinusoides de igual amplitud moviéndose en sentidos opuestos. | ||
| + | |||
| + | El principio de superposición im plica que, aunque cuando las dos señales coinciden en el espacio y el tiempo la solución resultante puede tener una aspecto muy complicado, una vez que separan cada una de las señales continúa sin cambios, como si no se hubiera encontrado con la otra. | ||
| + | |||
| + | ====Deducción de la ecuación de onda en una dimensión==== | ||
{{ac|Deducción de la ecuación de onda en una dimensión}} | {{ac|Deducción de la ecuación de onda en una dimensión}} | ||
| + | |||
| + | La expresión matemática de la ecuación de onda puede inducirse a partir de la solución. Partiendo del principio físico de que una onda es una propagación de una señal sin transmisión de materia, y de que las ondas pueden superponerse, se busca una ecuación diferencial tal que | ||
| + | |||
| + | * <math>f(x-vt)</math> es solución para todo <math>f</math> | ||
| + | * <math>g(x-vt)</math> es solución para todo <math>g</math> | ||
| + | * Una superposición <math>f(x-vt)+g(x+vt)</math> es solución para todo <math>f</math> y todo <math>g</math> | ||
| + | |||
| + | Imponiendo estas tres condiciones se llega a que la ecuación diferencial más sencilla que las verifica es la ecuación de onda. | ||
| + | |||
| + | ===En tres dimensiones=== | ||
| + | La ecuación de onda puede generalizarse al caso de una magnitud que depende de las tres coordenadas espaciales. En este caso la ecuación diferencial es | ||
| + | |||
| + | <center><math>\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2u}{\partial z^2}-\frac{1}{v^2}\frac{\partial^2 u}{\partial t^2}=0</math></center> | ||
| + | |||
| + | En el caso tridimensional, aunque <math>v</math> sigue siendo la velocidad de la onda, ya las soluciones no poseen la forma snecilla de funciones que se mueven sin deformarse. Por ejemplo, un sonido que se extiende desde una fuente puntual en todas las direcciones se va atenuando, a medida que la energía de la onda sonora se va expandiendo y alejándose de la fuente. | ||
==Ondas sinusoidales: ecuación de onda lineal== | ==Ondas sinusoidales: ecuación de onda lineal== | ||
| Línea 26: | Línea 147: | ||
===Ecuación para las ondas en una cuerda tensa=== | ===Ecuación para las ondas en una cuerda tensa=== | ||
{{ac|Ecuación para las ondas en una cuerda tensa}} | {{ac|Ecuación para las ondas en una cuerda tensa}} | ||
| + | ===Potencia y energía en una onda=== | ||
| + | {{ac|Potencia y energía en una onda}} | ||
==Superposición de ondas: principio de superposición== | ==Superposición de ondas: principio de superposición== | ||
{{ac|Superposición de ondas}} | {{ac|Superposición de ondas}} | ||
| + | |||
| + | ===Ondas estacionarias=== | ||
| + | {{ac|Ondas estacionarias}} | ||
| + | <center>[[Imagen:OEL.gif]]</center> | ||
| + | |||
| + | <center>[[Imagen:OET.gif]]</center> | ||
==Problemas== | ==Problemas== | ||
| Línea 36: | Línea 165: | ||
[[Categoría:Oscilaciones y ondas|20]] | [[Categoría:Oscilaciones y ondas|20]] | ||
[[Categoría:Física Aeronáuticos|110]] | [[Categoría:Física Aeronáuticos|110]] | ||
| + | [[Categoría:Física I (G.I.T.I.)]] | ||
última version al 15:43 7 sep 2010
Contenido |
1 Ondas mecánicas
2 Ondas transversales y longitudinales
2.1 Ondas longitudinales
En una onda longitudinal la vibración de las partículas se produce en la misma dirección en que se propaga la onda.
El caso más común de onda longitudinal es el de las ondas de compresión, en el que las partículas vibran en un sentido, tradmitiendo su vibración a las partículas adyacentes. A este tipo de ondas de compresión pertenece el sonido (en particular, para el caso de que el medio material sea el aire), y las ondas sísmicas P.
2.1.1 Onda sinusoidal
Cuando tenemos una oscilación periódica, cada partícula oscila en torno a su posición de equilibrio con una variación de la forma
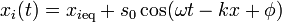
Aunque la onda avanza, observando cada una de las partículas individualmente, puede verse que en promedio cada una permanece inmóvil.

2.1.2 Pulso
Una onda (longitudinal o transversal) no tiene por qué ser necesariamente una sinusoide. Un golpe seco en un extremo de un material produce un pulso, que se mueve a lo largo de él. Este pulso es también una onda.

2.2 Ondas transversales
En una onda transversal cada partícula se mueve perpendicularmente a la dirección en que avanza la onda, de forma que para una onda sinusoidal sería
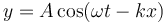
Más en general, una onda transversal es una combinación de una señal que se propaga en un sentido más una que se propaga en el sentido opuesto, lo cual se puede escribir en la forma general
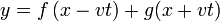
siendo f y g funciones arbitrarias de una variable (aunque si representan ondas físicas reales, además son acotadas).
2.2.1 Onda sinusoidal

2.2.2 Pulso

2.3 Combinaciones de ondas
Una onda puede ser una combinación de una onda longitudinal y una transversal, de forma que cada partícula describe un movimiento elíptico.
En particular, la trayectoria individual puede ser una circunferencia, esto es lo que ocurre para las ondas superficiales en agua (qque no son transversales, como suele suponerse), el movimiento de cada partícula es
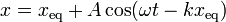
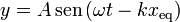

3 Ecuación de onda
Una onda puede definirse, de forma matemática, como una solución de la ecuación de onda, que es una ecuación diferencial concreta.
Si el análisis de una magnitud de un sistema físico conduce a una ecuación diferencial de la misma forma que la ecuación de onda, se puede concluir que la solución para dicha magnitud es un comportamiento ondulatorio, aunque no se trate de un sistema mecánico y no haya verdadero movimiento de partículas (esto es lo que ocurre, por ejemplo, con las ondas electromagnéticas).
3.1 En una dimensión
Si tenemos una magnitud u que depende de una coordenada x y del tiempo, esta magnitud presenta comportamiento ondulatorio si se satisface la ecuación diferencial en derivadas parciales
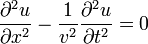
siendo v la velocidad de la onda.
- Ondas en una cuerda tensa
- Por ejemplo, en el caso de una cuerda tensa puede demostrarse que los movimientos transversales verifican la ecuación
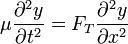
- siendo μ la densidad lineal de masa y FT la tensión de la cuerda. Reescribiendo esta ecuación como
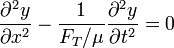
- vemos que el movimiento de la cuerda tensa es ondulatorio, siendo su velocidad
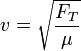
- Ondas electromagnéticas
- Al analizar el comportamiento de los campos eléctricos y magnéticos dependientes del tiempo, Maxwell llegó a la conclusión de que en el espacio vacío un campo eléctrico dependiente de una sola coordenada verifica la ecuación
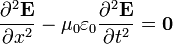
- siendo
 y μ0 dos constantes físicas denominadas permitividad y permeabilidad del vacío:
y μ0 dos constantes físicas denominadas permitividad y permeabilidad del vacío:
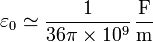
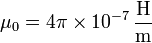
- De esta ecuación resulta que el campo eléctrico (y el magnético) tiene un comportamiento ondulatorio, siendo su velocidad
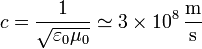
- que es exactamente la velocidad de la luz. De esto Maxwell concluyó que la luz es una onda electromagnético.
3.1.1 Principio de superposición
Una propiedad importante de la ecuación de onda es que es lineal, esto es, que verifica el principio de superposición: si u1 y u2 son dos soluciones, cualquier superposición
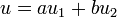
con a y b constantes es también una solución.
3.1.2 Solución general de la ecuación de onda
Puede demostrarse que la solución general de la ecuación de onda
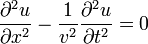
es una función de la forma
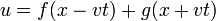
siendo f y g dos funciones cualesquiera de una variable. No obstante, para una onda real de un sistema físico no pueden ser cualesquiera, sino que deben ser continua, derivable y acotada (no irse a infinito). Aun así, esto dejea mucha libertad a las soluciones: pulsos, ondas viajeras y estacionarias son soluciones de la ecuación de onda.
En particular, si g = 0 nos queda la solución
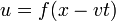
que es una onda viajera que se propaga hacia x creciente. Esta onda conserva su forma (ya que f(s) es siempre la misma, solo va cambiando su posición)
Si f = 0, la solución es de la forma
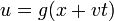
que es una onda viajera propagándose hacia los valores de x decrecientes
En el caso general, la solución es una superposición de una señal que se propaga hacia la derecha con una que se propaga hacia la izquierda. Así, por ejemplo, una onda estacionaria puede verse como la suma de dos sinusoides de igual amplitud moviéndose en sentidos opuestos.
El principio de superposición im plica que, aunque cuando las dos señales coinciden en el espacio y el tiempo la solución resultante puede tener una aspecto muy complicado, una vez que separan cada una de las señales continúa sin cambios, como si no se hubiera encontrado con la otra.
3.1.3 Deducción de la ecuación de onda en una dimensión
La expresión matemática de la ecuación de onda puede inducirse a partir de la solución. Partiendo del principio físico de que una onda es una propagación de una señal sin transmisión de materia, y de que las ondas pueden superponerse, se busca una ecuación diferencial tal que
- f(x − vt) es solución para todo f
- g(x − vt) es solución para todo g
- Una superposición f(x − vt) + g(x + vt) es solución para todo f y todo g
Imponiendo estas tres condiciones se llega a que la ecuación diferencial más sencilla que las verifica es la ecuación de onda.
3.2 En tres dimensiones
La ecuación de onda puede generalizarse al caso de una magnitud que depende de las tres coordenadas espaciales. En este caso la ecuación diferencial es
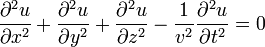
En el caso tridimensional, aunque v sigue siendo la velocidad de la onda, ya las soluciones no poseen la forma snecilla de funciones que se mueven sin deformarse. Por ejemplo, un sonido que se extiende desde una fuente puntual en todas las direcciones se va atenuando, a medida que la energía de la onda sonora se va expandiendo y alejándose de la fuente.
4 Ondas sinusoidales: ecuación de onda lineal
5 Ondas sinusoidales en una cuerda: velocidad y energía transmitida
5.1 Ecuación para las ondas en una cuerda tensa
5.2 Potencia y energía en una onda
6 Superposición de ondas: principio de superposición
6.1 Ondas estacionarias