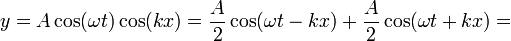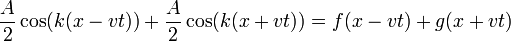Deducción de la ecuación de onda en una dimensión

De Laplace

Contenido

1 Objetivo
2 Ondas hacia la derecha
3 Ondas hacia la izquierda
4 Superposición
5 Derivando una vez
6 Derivando dos veces
7 Redefinición de onda

1 Objetivo

Nuestro objetivo es hallar la ecuación diferencial que deben verificar las soluciones para las ondas en una dimensión. Debe cumplir los siguientes requisitos:

2 Ondas hacia la derecha

Debe admitir como soluciones las de la forma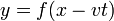 $y = f(x-vt)\,$

que representan señales que se propagan hacia la derecha sin deformarse.

3 Ondas hacia la izquierda

Una cuerda, u otro sistema vibrante, normalmente es simétrica respecto al sentido de propagación de las ondas. No hay diferencia entre agitar el extremo de la izquierda y producir una onda que se mueve hacia la derecha, que agitar el de la derecha y que la onda resultante se mueva hacia la izquierda.

Por tanto, la ecuación diferencial buscada debe admitir también soluciones de la forma

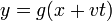
$y = g(x+vt)\,$

con $g$ una función arbitraria.

4 Superposición

La ecuación resultante debe admitir además que sobre la misma cuerda vibrante se propaguen simultáneamente dos o más señales, sin afectarse mutuamente. Por ello la solución general debe ser de la forma

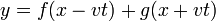
$y = f(x-vt) + g(x+vt)\,$

5 Derivando una vez

La solución general es una función de dos variables, x y t, siendo la velocidad de las ondas una constante. Necesitamos una ecuación que ligue las derivadas parciales respecto a la posición y respecto al tiempo.

5.1 Derivando respecto al espacio y al tiempo

Comenzamos con las soluciones de la forma $y = f (x - v t)$ , donde $f$ es una función arbitraria de una sola variable, esto es que podemos escribir estas soluciones en la forma

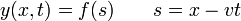
$y(x,t) = f(s)\qquad s = x - vt$

esto es, y depende de x y t no de cualquier forma, sino a través de la combinación definida por s. Si ahora derivamos respecto a la posición x, aplicando la regla de la cadena

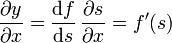
$\frac{\partial y}{\partial x} = \frac{\mathrm{d}f}{\mathrm{d}s}\,\frac{\partial s}{\partial x} = f'(s)$

ya que

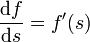
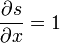
$\frac{\mathrm{d}f}{\mathrm{d}s}=f'(s)$ $\frac{\partial s}{\partial x} = 1$

Si derivamos respecto al tiempo, nos resulta

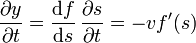
$\frac{\partial y}{\partial t} = \frac{\mathrm{d}f}{\mathrm{d}s}\,\frac{\partial s}{\partial t} = -v f'(s)$

donde la derivada de s respecto al tiempo vale

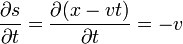
$\frac{\partial s}{\partial t} = \frac{\partial(x-vt)}{\partial t}= -v$

Eliminando $f'(s)$ entre las dos derivadas obtenemos la relación

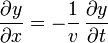
$\frac{\partial y}{\partial x}=-\frac{1}{v}\,\frac{\partial y}{\partial t}$

Esta ecuación en derivadas parciales la verifican todas las soluciones de la forma $y = f (x - v t)$ . Sin embargo, como veremos, eso no es suficiente para nuestros objetivos.

5.2 El problema del signo

La ecuación anterior nos vale para las ondas que viajan hacia la izquierda, pero no para las que van hacia la derecha. Si realizamos un análisis similar para las soluciones de la forma

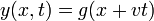
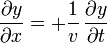
$y(x,t) = g(x+vt)\,$ $\Rightarrow$ $\frac{\partial y}{\partial x}=+\frac{1}{v}\,\frac{\partial y}{\partial t}$

que no es la misma ecuación que en el caso anterior. Por ello, no nos vale ni una ni la otra, pues deseamos una ecuación que valga para los dos a la vez.

5.3 ¿Elevar al cuadrado?

Una posibilidad de eliminar el problema del signo es elevar al cuadrado los dos miembros, de forma que obtenemos la ecuación diferencial

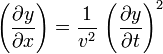
$\left(\frac{\partial y}{\partial x}\right)=\frac{1}{v^2}\,\left(\frac{\partial y}{\partial t}\right)^2$

Esta ecuación la verifican tanto las soluciones de la forma $f (x - v t)$ como las de la forma $g (x + v t)$ , pero no la combinación de ambas $f (x - v t) + g (x - v t)$ , por lo que tampoco nos vale.

Por ejemplo, consideremos las funciones sencillas

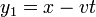
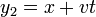
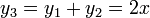
$y_1= x-vt\,$ $y_2=x+vt\,$ $y_3=y_1+y_2 = 2x\,$

Para la primera tenemos

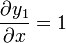
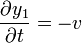
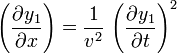
$\frac{\partial y_1}{\partial x} = 1$ $\frac{\partial y_1}{\partial t} = -v$ $\Rightarrow$ $\left(\frac{\partial y_1}{\partial x}\right)=\frac{1}{v^2}\,\left(\frac{\partial y_1}{\partial t}\right)^2$

Del mismo modo, para la segunda

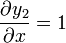
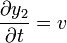
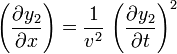
$\frac{\partial y_2}{\partial x} = 1$ $\frac{\partial y_2}{\partial t} = v$ $\Rightarrow$ $\left(\frac{\partial y_2}{\partial x}\right)=\frac{1}{v^2}\,\left(\frac{\partial y_2}{\partial t}\right)^2$

Pero, para la tercera

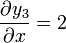
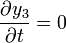
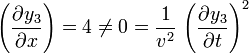
$\frac{\partial y_3}{\partial x} = 2$ $\frac{\partial y_3}{\partial t} = 0$ $\Rightarrow$ $\left(\frac{\partial y_3}{\partial x}\right)=4\neq 0 = \frac{1}{v^2}\,\left(\frac{\partial y_3}{\partial t}\right)^2$

Por tanto, debemos seguir buscando una ecuación más general.

6 Derivando dos veces

Volvamos a las soluciones de la forma $y = f (x - v t)$ , y calculemos su segunda derivada respecto a la posición

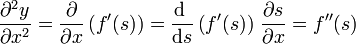
$\frac{\partial^2 y}{\partial x^2} = \frac{\partial }{\partial x}\left(f'(s)\right) = \frac{\mathrm{d}\ }{\mathrm{d}s}\left(f'(s)\right)\,\frac{\partial s}{\partial x} = f''(s)$

Si derivamos respecto al tiempo, nos resulta

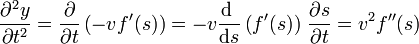
$\frac{\partial^2 y}{\partial t^2} = \frac{\partial }{\partial t}\left(-vf'(s)\right) = -v\frac{\mathrm{d}\ }{\mathrm{d}s}\left(f'(s)\right)\,\frac{\partial s}{\partial t} = v^2f''(s)$

Eliminando $f''(s)$ entre las dos derivadas obtenemos la relación

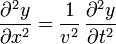
$\frac{\partial^2 y}{\partial x^2}=\frac{1}{v^2}\,\frac{\partial^2 y}{\partial t^2}$

Veamos si esta ecuación nos vale.

Según acabamos de ver, es satisfecha por las funciones de la forma

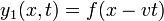
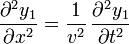
$y_1(x,t) = f(x-vt)\,$ $\Rightarrow$ $\frac{\partial^2 y_1}{\partial x^2}=\frac{1}{v^2}\,\frac{\partial^2 y_1}{\partial t^2}$

Puesto que la velocidad aparece al cuadrado, también es satisfecha por las ecuaciones que viajan hacia la izquierda

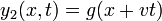
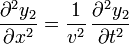
$y_2(x,t) = g(x+vt)\,$ $\Rightarrow$ $\frac{\partial^2 y_2}{\partial x^2}=\frac{1}{v^2}\,\frac{\partial^2 y_2}{\partial t^2}$

Al ser la derivada de la suma la suma de las derivadas, también es satisfecha por una combinación de las soluciones anteriores

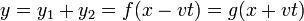
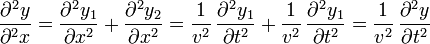
$y=y_1+y_2=f(x-vt) = g(x+vt)\,$ $\Rightarrow$ $\frac{\partial^2 y}{\partial^2 x}=\frac{\partial^2 y_1}{\partial x^2}+\frac{\partial^2 y_2}{\partial x^2}=\frac{1}{v^2}\,\frac{\partial^2 y_1}{\partial t^2}+\frac{1}{v^2}\,\frac{\partial^2 y_1}{\partial t^2}=\frac{1}{v^2}\,\frac{\partial^2 y}{\partial t^2}$

Puesto que cumple todas las condiciones, esta sí es la ecuación que estamos buscando.

7 Redefinición de onda

7.1 Ecuación de onda

Reescribiendo el resultado anterior, tenemos que la ecuación de onda en una dimensión es

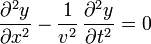
$\frac{\partial^2 y}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2y}{\partial t^2}=0$

El procedimiento, a partir de este punto, es darle la vuelta al razonamiento. Se define la ecuación de onda como esta ecuación diferencial.

7.2 Definición de onda

A partir de la ecuación anterior, una onda se define matemáticamente como una solución de la ecuación de onda.

Puede demostrarse que la solución general de esta ecuación es de la forma

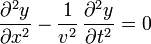
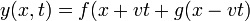
$\frac{\partial^2 y}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2y}{\partial t^2}=0$ $\Rightarrow$ $y(x,t)=f(x+vt+g(x-vt)\,$

esto es, que no hay más soluciones que las que ya conocemos.

Hay que señalar que, al ser $f$ y $g$ funciones arbitrarias, la forma de la solución $y (x, t)$ puede ser muy diversa. En particular no tiene por qué resultar una onda viajera.

7.3 Una onda que no viaja

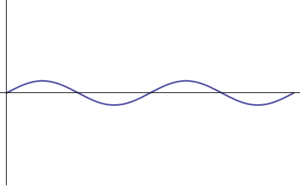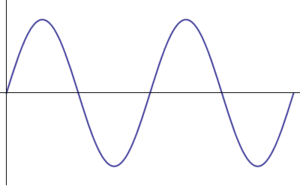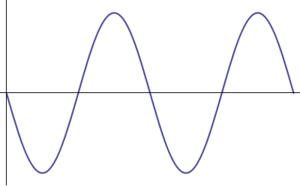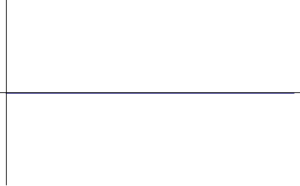
Por ejemplo, la onda estacionaria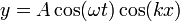 $y = A\cos(\omega t)\cos(k x)\,$

en la que las crestas no se desplazan, sino que simplemente suben y bajan, es una onda, ya que es solución de la ecuación diferencial.

Las segundas derivadas valen

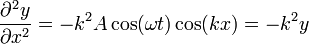
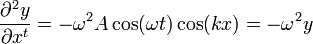
$\frac{\partial^2y}{\partial x^2} = -k^2A\cos(\omega t)\cos(k x)=-k^2y$ $\frac{\partial^2y}{\partial x^t} = -\omega^2A\cos(\omega t)\cos(k x)=-\omega^2y$

Sustituyendo en la ecuación de onda

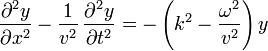
$\frac{\partial^2y}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2y}{\partial t^2} = -\left(k^2-\frac{\omega^2}{v^2}\right)y$

que se anula si hacemos

$v = \frac{\omega}{k}$

Podemos comprobar que esta solución estacionaria es una combinación de una onda que viaja a la derecha y otra que viaja hacia la izquierda. $y = A\cos(\omega t)\cos(k x) = \frac{A}{2}\cos(\omega t-kx)+\frac{A}{2}\cos(\omega t+ kx) =$ $\frac{A}{2}\cos(k(x-vt))+\frac{A}{2}\cos(k(x+vt)) = f(x-vt)+g(x+vt)$

Deducción de la ecuación de onda en una dimensión

De Laplace

Contenido

1 Objetivo

2 Ondas hacia la derecha

3 Ondas hacia la izquierda

4 Superposición

5 Derivando una vez

5.1 Derivando respecto al espacio y al tiempo

5.2 El problema del signo

5.3 ¿Elevar al cuadrado?

6 Derivando dos veces

7 Redefinición de onda

7.1 Ecuación de onda

7.2 Definición de onda

7.3 Una onda que no viaja

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES