Batidos en un piano
De Laplace
1 Enunciado
Para las notas agudas de los pianos se emplean cuerdas dobles o triples, formadas por hilos de acero paralelos. El La de la octava menor (110 Hz) está formado por dos hilos, tensados teóricamente a 600 N. Uno de los dos hilos se destensa ligeramente y al tocar la tecla se oyen batidos con una frecuencia de 4 Hz. ¿Cuál es la tensión de la cuerda destensada?
2 Solución
La tensión a la que se haya sometida una cuerda de longitud L, diámetro D y densidad volumétrica de masa ρ es
siendo f la frecuencia de vibración. De aquí que si tenemos dos cuerdas idénticas que vibran a distinta frecuencia, la relación entre sus tensiones es
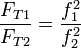
En nuestro caso, una de las cuerdas vibra a frecuencia 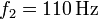 y se encuentra a
y se encuentra a 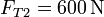 de tensión. La otra se ha destensado y vibra, por tanto, a una frecuencia menor. La diferencia entre las dos frecuencias la da la frecuencia de los batidos o pulsaciones
de tensión. La otra se ha destensado y vibra, por tanto, a una frecuencia menor. La diferencia entre las dos frecuencias la da la frecuencia de los batidos o pulsaciones
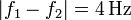

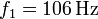
y por tanto la tensión de esta cuerda es