Coordenadas cilíndricas. Base vectorial

De Laplace

última version al 17:18 13 abr 2010

1 Base vectorial

Con ayuda de un poco de trigonometría construimos la base vectorial de cilíndricas.

• Antes de eso, recordamos que la coordenada es la misma en cilíndricas que en esféricas, por lo que comparte el vector unitario

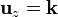
• Para 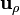y 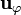consideramos un triángulo rectángulo en

el plano horizontal que pasa por . Al aumentar la coordenada 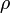nos movemos a lo largo de la hipotenusa, por lo que

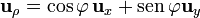
• El vector 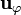es tangente a la circunferencia que pasa por , y por tanto perpendicular a la hipotenusa

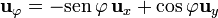
2 Base ortonormal dextrógira

Los vectores de la base cilíndrica forman una base ortonormal dextrógira si las coordenadas se ordenan en la forma . Los productos escalares y vectoriales vienen dados por las siguientes tablas de multiplicar

·
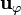
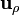
	1	0	0
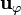
	0	1	0
	0	0	1

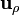
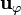
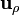
	0
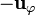
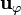
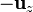
		0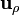
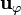
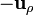
			0

3 Factores de escala

• El factor de escala de la coordenada es el mismo que en cartesianas

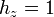
• La coordenada ρ es una distancia, por lo que variar una cantidad 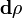equivale a recorrer una distancia 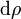y

• La coordenada 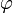es, en cambio, es un ángulo. Al variar la coordenada en sobre una circunferencia de radio 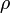, la

distancia recorrida es 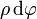y el factor de escala es

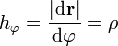
3.1 ¡Ojo a la dirección de los vectores!

Los vectores 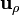y 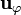son funciones de la coordenada 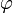. Eso quiere decir que, dependiendo del punto que estemos considerando, apuntan en un sentido u otro. En particular, si consideramos dos puntos diametralmente opuestos respecto al eje 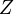, el vector 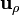en el primer punto es exactamente el opuesto que en el otro, esto es, que "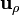" no significa siempre lo mismo, ya que

4 Enlaces

• Siguiente: Coordenadas esféricas. Base vectorial
• Anterior: Coordenadas cartesianas. Base vectorial
• Coordenadas cilíndricas. Definición
• Coordenadas cilíndricas. Líneas y superficies coordenadas