Movimiento ondulatorio
De Laplace
(→Ondas sinusoidales en una cuerda: velocidad y energía transmitida) |
(→Onda sinusoidal) |
||
| Línea 9: | Línea 9: | ||
Cuando tenemos una oscilación periódica, cada partícula oscila en torno a su posición de equilibrio con una variación de la forma | Cuando tenemos una oscilación periódica, cada partícula oscila en torno a su posición de equilibrio con una variación de la forma | ||
| - | <center><math>x_i(t) = x_{i\mathrm{eq}} + | + | <center><math>x_i(t) = x_{i\mathrm{eq}} + s_0 \cos(\omega t - k x + \phi)\,</math></center> |
| - | Aunque la onda avanza, | + | Aunque la onda avanza, observando cada una de las partículas individualmente, puede verse que en promedio cada una permanece inmóvil. |
<center>[[Imagen:Ondalongitudinal.gif]]</center> | <center>[[Imagen:Ondalongitudinal.gif]]</center> | ||
Revisión de 18:31 27 mar 2010
Contenido |
1 Ondas mecánicas
2 Ondas transversales y longitudinales
2.1 Ondas longitudinales
En una onda longitudinal la vibración de las partículas se produce en la misma dirección en que se propaga la onda.
El caso más común de onda longitudinal es el de las ondas de compresión, en el que las partículas vibran en un sentido, tradmitiendo su vibración a las partículas adyacentes. A este tipo de ondas de compresión pertenece el sonido (en particular, para el caso de que el medio material sea el aire), y las ondas sísmicas P.
2.1.1 Onda sinusoidal
Cuando tenemos una oscilación periódica, cada partícula oscila en torno a su posición de equilibrio con una variación de la forma
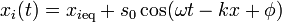
Aunque la onda avanza, observando cada una de las partículas individualmente, puede verse que en promedio cada una permanece inmóvil.

2.1.2 Pulso
Una onda (longitudinal o transversal) no tiene por qué ser necesariamente una sinusoide. Un golpe seco en un extremo de un material produce un pulso, que se mueve a lo largo de él. Este pulso es también una onda.

2.2 Ondas transversales
2.2.1 Onda sinusoidal

2.2.2 Pulso

2.3 Combinaciones de ondas

3 Función de onda
3.1 Expresión general de la ondas unidimensionales
3.2 Deducción de la ecuación de onda en una dimensión
4 Ondas sinusoidales: ecuación de onda lineal
5 Ondas sinusoidales en una cuerda: velocidad y energía transmitida
5.1 Ecuación para las ondas en una cuerda tensa
5.2 Potencia y energía en una onda
6 Superposición de ondas: principio de superposición
6.1 Ondas estacionarias







