De Laplace

Contenido

1 Problemas de boletín
2 Problemas adicionales
3 Preguntas de test

1 Problemas de boletín

1.1 Ejemplos de cálculo de dimensiones

A partir de las relaciones definitorias

Velocidad	Cantidad de movimiento	Aceleración	Fuerza
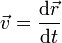
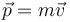
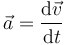
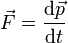
$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}$	$\vec{p}=m\vec{v}$	$\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}$	$\vec{F}=\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}$
Trabajo	Potencia	Momento cinético	Momento de una fuerza
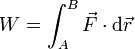
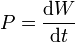
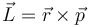
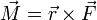
$W=\int_A^B\vec{F}\cdot\mathrm{d}\vec{r}$	$P=\frac{\mathrm{d}W}{\mathrm{d}t}$	$\vec{L}=\vec{r}\times\vec{p}$	$\vec{M}=\vec{r}\times\vec{F}$

determine las ecuaciones dimensionales de estas magnitudes, así como sus unidades en el Sistema Internacional (SI) en función de las unidades fundamentales de este sistema.

1.2 Fórmulas posiblemente con dimensiones incorrectas

Teniendo en cuenta las dimensiones calculadas en el problema anterior, indique cuáles de las siguientes expresiones son necesariamente incorrectas:

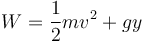
a) $\displaystyle W = \frac{1}{2}mv^2 + gy$

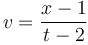
b) $\displaystyle v=\frac{x-1}{t-2}$

c) $\displaystyle P = m\frac{(v^2/R - a)}{(t-x/v)}(x-\pi R^2)$

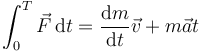
d) $\displaystyle \int_0^T \vec{F}\,\mathrm{d}t = \frac{\mathrm{d}m}{\mathrm{d}t}\vec{v}+ m\vec{a}t$

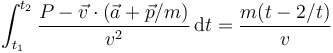
e) $\displaystyle \int_{t_1}^{t_2}\frac{P-\vec{v}\cdot(\vec{a}+\vec{p}/m)}{v^2}\,\mathrm{d}t = \frac{m(t-2/t)}{v}$

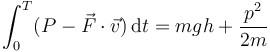
f) $\displaystyle \int_0^T (P-\vec{F}\cdot\vec{v})\,\mathrm{d}t = mgh + \frac{p^2}{2m}$

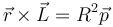
g) $\vec{r}\times\vec{L} = R^2\vec{p}$

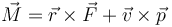
h) $\displaystyle \vec{M} = \vec{r}\times\vec{F}+\vec{v}\times\vec{p}$

1.3 Dimensiones de constantes en una ecuación

Una partícula se mueve según la ley

$x = A\left(\mathrm{e}^{Bt}-C\right)$

¿Cuáles son las dimensiones de $A$ , $B$ y $C$ ? ¿Cuáles son sus unidades en el SI?

1.4 Dimensiones y unidades en el oscilador amortiguado

Un oscilador amortiguado obedece la ley de movimiento

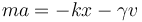
$ma = -kx -\gamma v\,$

¿Cuáles son las dimensiones de $k$ y $γ$ ? ¿Cuáles sus unidades en el SI?

1.5 Ejemplo de estimación de longitudes y volúmenes

Se tiene un bloque de aluminio de forma cúbica cuya masa es aproximadamente 2.5 kg. Estime el valor de la arista del cubo, así como su superficie lateral. Si se sabe que la incertidumbre de la medida de la masa es de 100 g, ¿entre qué valores se hallarán la arista y el área lateral?

¿Y si en vez de aluminio fuera oro?

2 Problemas adicionales

2.1 Conversión de unidades no del SI

Exprese las siguientes unidades en el sistema internacional. Consulte las definiciones en la red o la bibliografía

1 nudo
1 psi (pound-per-square-inch)
1 año-luz
1 acre

2.2 Ejemplos de estimaciones numéricas

Estime el orden de magnitud de las siguientes cantidades:

Número de litros de gasolina que se consumen en España en un año
La cantidad de agua que hay en la Tierra. Si toda ella se concentrara en una esfera, ¿cuál sería su radio?
Masa de una hormiga
Vueltas que da una rueda de un coche en un trayecto Sevilla-Madrid.
El número de latidos del corazón de una persona a lo largo de su vida.
Las bolas que hay en la máquina de la figura.
La velocidad de reproducción en bits/s de un CD de música.

2.3 Estimación del radio terrestre

De un lago se sabe que tiene 6 km de anchura. Desde un punto de una orilla no se ve la otra, pero se comprueba que subiendo al balcón del primer piso, sí se ve. Estime el radio de la Tierra.

2.4 Ejemplos de órdenes de magnitud

Indique valores para los ordenes de magnitud de las siguientes longitudes, masas o tiempos, en el SI.

Longitudes

1. Bacteria — 2. Ser humano — 3. Distancia Tierra-Sol — 4. Circunferencia terrestre — 5. Átomo — 6. España — 7. Espesor de un folio — 8. Distancia a α-Centauri — 9. Núcleo atómico — 10. Altura a la que se encuentra la ISS

Masas

1. Bacteria — 2. Ser humano — 3. Tierra — 4. Hormiga — 5. Sol — 6. Montaña más alta — 7. Folio — 8. Agua de una piscina olímpica — 9. Núcleo atómico — 10. Elefante adulto

Tiempos

1. Día — 2. Año — 3. Vida humana — 4. Latido de un corazón — 5. Tiempo que la luz tarda en recorrer 1 m — 6. Edad de la Tierra — 7. Parpadeo — 8. Aleteo de un colibrí — 9. Consulta a un disco duro — 10. Civilización

2.5 Ejemplos de valores numéricos

Las siguientes cantidades representan aproximadamente los valores de las magnitudes de la tabla, expresadas en las unidades fundamentales del SI o productos de ellas. Indique cuál le corresponde a cada una, indicando sus unidades.

1	Peso de una persona	2	Densidad de masa del agua	3	Aceleración de la Tierra alrededor del Sol
4	Masa de la Tierra	5	Diámetro de un glóbulo rojo	6	Distancia Tierra-Sol
7	Altura a la que se encuentra la Estación Espacial Internacional	8	Radio de un átomo	9	Densidad del oro
10	Diámetro de una pelota de golf	11	Espesor de un folio	12	Aceleración de la gravedad
13	Arista de un cubo que contuviera todo el oro del mundo	14	Velocidad de Usain Bolt en los 100m	15	Masa de un m³ de agua
16	Duración de un año	17	Velocidad de una bacteria	18	Periodo de la corriente alterna doméstica
19	Masa del electrón	20	Velocidad de la luz	21	Circunferencia terrestre

A	10⁻³⁰	B	10⁻¹⁰	C	6×10⁻⁶
D	5×10⁻⁵	E	6×10⁻⁵	F	6×10⁻³
G	2×10⁻²	H	5×10⁻²	I	10
J	10	K	20	L	8× 10²
M	10³	N	10³	P	2×10⁴
Q	4×10⁵	R	3×10⁷	S	4×10⁷
T	3×10⁸	U	1.5×10¹¹	V	6×10²⁴

2.6 Dependencias del periodo de un péndulo

Un péndulo simple es una masa $m$ suspendida de un hilo ideal (sin masa), que tiene una longitud $l$ . La masa está sometida a la aceleración de la gravedad, $g$ . El péndulo llega a separarse de la vertical un cierto ángulo $θ 0$ .

Si duplicamos la longitud del péndulo, ¿cómo cambiará su periodo de oscilación? ¿Y si nos llevamos el péndulo a la Luna, donde la gravedad es 1/6 de la terrestre?

2.7 Conversión de unidades del sistema imperial

Exprese las siguientes unidades del sistema imperial (británico) en el sistema internacional, sabiendo que 1 pulgada = 2.54 cm y que 1 libra = 0.4356 kg:

1 pie = 12 pulgadas
1 yarda = 3 pies
1 milla = 1760 yardas
1 acre = rectángulo de 220 yardas por 22 yardas
1 libra-fuerza = peso de una libra
1 psi = 1 libra/pulgada²
1 piedra = 14 libras

3 Preguntas de test

3.1 Longitud de un pársec

Un pársec vale, aproximadamente, 3.26 años-luz, siendo un año-luz la distancia recorrida por la luz en un año. ¿A qué equivale un pársec en el Sistema Internacional?

A 3.08×10¹³m
B 9.46×10¹⁵m
C 5.14×10¹⁴m
D 3.08×10¹⁶m

3.2 Dimensiones de constantes

Una partícula se mueve en línea recta, cumpliendo su velocidad instantánea

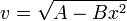
$v = \sqrt{A- B x^2}$

con $A$ y $B$ constantes positivas. ¿En que se medirá $B$ en el SI?

A m⁻²s⁻²
B m⁴/s²
C s⁻²
D m²/s⁴

3.3 Masa de una bacteria

Una bacteria es una partícula más o menos esférica con un diámetro del orden de 1μm ¿Cuál es el orden de magnitud de la masa de una bacteria?

A Picogramos.
B Nanogramos.
C Femtogramos.
D Microgramos.

3.4 Tamaño de una baldosa

Se mide el lado de una baldosa cuadrada y se obtiene que mide 33.3 cm. ¿Cuál es la expresión correcta de la longitud de su diagonal?

A: 47.1 cm
B 50 cm
C 47.09331 cm
D 47.0933116270 cm

3.5 Masa de una micra cúbica

Una micra (μm) es una milésima de milímetro. Si la densidad del agua es 1000 kg/m³, ¿cuál es la masa de 1μm³ de agua?

A un microgramo.
B un picogramo.
C un nanogramo.
D una milésima de picogramo.

3.6 Incertidumbre de un volumen

Se tiene un cubo cuya arista mide 1 m, con una incertidumbre de 1 cm. ¿Cuánto es aproximadamente la incertidumbre de su volumen?

A 3 cm³
B 100 cm³
C 1 cm³
D 30000 cm³

3.7 Altura de una persona

Los americanos suelen medir la altura de las personas en pies (') y pulgadas("), siendo un pie igual a 12 pulgadas y una pulgada igual a 2.54 cm. Si un hombre dice: Mido 5'1". podríamos decir que ese hombre…

A mide lo mismo que un pivot típico de la NBA.
B tiene una estatura inferior a la media.
C es relativamente alto.
D tiene una estatura media

3.8 Cantidad de agua ingerida

¿Cual de las siguientes es una estimación más aproximada de la cantidad de agua (sola o combinada) que ingiere una persona a lo largo de su vida?

A 0.5 Hm³
B 5000 dm³
C 50 m³
D 50000 m³

3.9 Velocidad de la luz

Se construye un sistema de unidades basado en el palmo (1 palmo = 20cm), el rato (1 rato = 15 minutos) y el puñado (1 puñado = 100 gramos). En este sistema, ¿cuánto vale la velocidad de la luz?

A 1.35 terapalmos/rato
B 81 terapalmos/rato
C 81 gigapalmos/rato
D 1.35 gigapalmos/rato

3.10 Masa de la Giralda

¿Cuál es el orden de magnitud de la masa de la Giralda?

A 10⁹kg
B 10⁷kg
C 10⁵kg
D 10⁴kg

3.11 Comparación de densidades de población

Una milla (mi) son 1609.344 m. La densidad de población en los Estados Unidos es de 84.09 hab/mi², mientras que la de España es de 93 hab/km². Por tanto, la densidad de población en España es…

A 1.10 veces la de Estados Unidos
B 0.42 veces la de Estados Unidos
C 2.86 veces la de Estados Unidos
D 1.78 veces la de Estados Unidos

3.12 Incertidumbre relativa

De un bloque de un material homogéneo se conoce su masa con una gran precisión, pero su volumen se conoce con una incertidumbre relativa del 1%. Si calculamos la densidad del material como $M / V$ la incertidumbre relativa de ésta es aproximadamente…

A -1%
B No tenemos información suficiente para saberla
C 2%
D 1%

Problemas de introducción a la física (GIE)