Estimación del radio terrestre

De Laplace

1 Enunciado

De un lago se sabe que tiene 6 km de anchura. Desde un punto de una orilla no se ve la otra, pero se comprueba que subiendo al balcón del primer piso, sí se ve. Estime el radio de la Tierra.

2 Solución

Lo que nos dice el enunciado es que la distancia a la que se encuentra el horizonte es de unos 6 km cuando nos encontramos a una altura de un primer piso (que vienen a ser unos 3 m).

Ahora bien, ¿cuál es la fórmula que relaciona la distancia a la que se halla el horizonte con la altura del punto de observación? ¿Cómo depende esta fórmula del radio terrestre?

El horizonte se encuentra sobre la tangente a la superficie terrestre desde el punto de observación. Los puntos más alejados quedan ocultos por la curvatura terrestre.

Suponiendo una Tierra esférica, construimos un triángulo rectángulo formado por un radio terrestre, la distancia al punto de observación y un radio prolongado en la altura h. Por el teorema de Pitágoras

Desarrollando y despejando

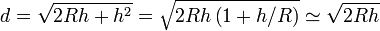
El último término es despreciable, ya que la altura del punto de observación (3m) es mucho menor que el radio terrestre (miles de kilómetros). Despejando de aquí

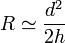
Sustituyendo las estimaciones del enunciado queda

El valor del radio terrestre medio es de 6370 km, por lo que vemos que una sola medida nos da ya una buena estimación de su orden de magnitud.