Máquinas térmicas (GIE)
De Laplace
Contenido |
1 El primer principio en procesos cíclicos
El primer principio de la termodinámica establece que en todo sistema físico y para todo proceso
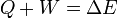
siendo Q y W respectivamente el calor y el trabajo que entran en el sistema por su frontera y E la energía total del sistema, que incluye potencial, cinética y todo el resto que englobamos en el concepto de energía interna.
Un proceso cíclico es uno en el que el estado final es el mismo que el inicial, o que se repite periódicamente. Los procesos cíclicos son la base de todas las máquinas y motores, que operan de forma periódica. En un proceso cíclico la energía total al final del proceso es la misma que al principio, por tratarse de una función de estado. Por tanto
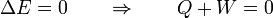
Si desglosamos el calor y el trabajo entre lo que entra y lo que sale

nos queda
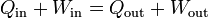
lo que nos dice que en un proceso cíclico lo que entra es igual a lo que sale.
No todos los términos son no nulos en todas las ocasiones.
En un motor eléctrico ideal, por ejemplo, en el sistema (el motor) entra trabajo eléctrico y sale trabajo mecánico, sin que haya calor implicado.
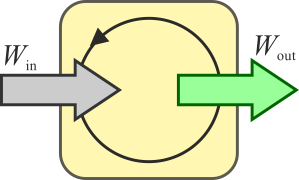
En un motor real, la situación anterior no es posible. Siempre hay factores que disipan energía en forma de calor como las resistencias eléctricas y el rozamiento. Esto provoca que no salga tanto trabajo como el que entra, y una parte se escapa en forma de calor disipado al ambiente. Para que fluya calor desde el sistema al ambiente, éste debe estar a una temperatura más baja que el sistema (lo que es lo habitual, ya que en los motores se alcanzan altas temperaturas). Por ello, el calor desechado va al “foco frío”.


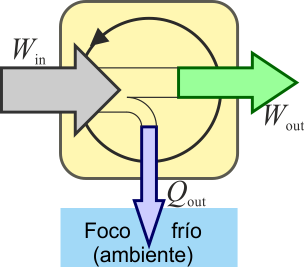
Definimos entonces el rendimiento o eficiencia de una máquina, de manera general, como
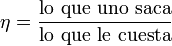
que, en el caso de un motor eléctrico real sería
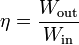
En una estufa de resistencia, en cambio, todo el trabajo que entra sale en forma de calor.

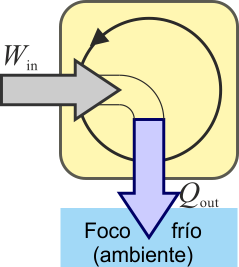
El rendimiento de esta estufa sería
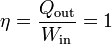
2 Máquina térmica
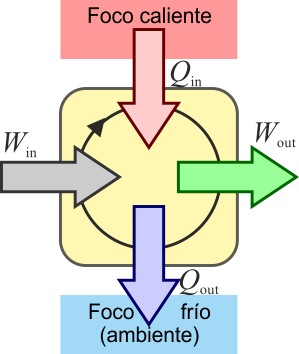
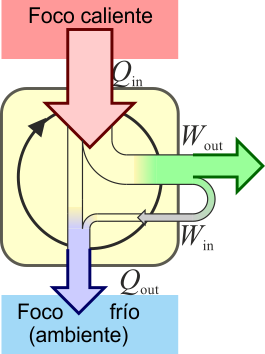
El mismo principio anterior se puede aplicar a un dispositivo que transforma calor en trabajo. Una máquina térmica es un dispositivo que, operando de forma cíclica, toma de calor de un foco caliente, realiza un cierto trabajo (parte del cual se emplea en hacer funcionar la propia máquina) y entrega calor de desecho a un foco frío, normalmente el ambiente.
2.1 Máquina de vapor
El ejemplo característico de máquina térmica es la máquina de vapor, que se emplea en la mayoría de las centrales eléctricas (sean estas térmicas, termo-solares o nucleares).
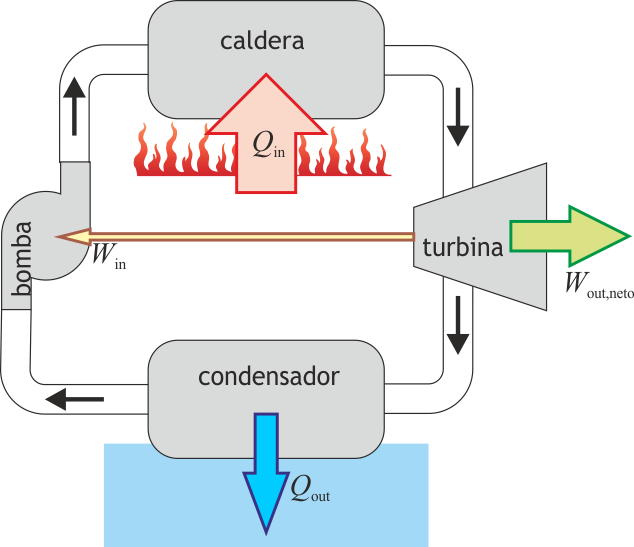
En su esquema más simple, una máquina de vapor está formada por cuatro elementos:
- Una bomba que mueve el líquido y mantiene el sistema en funcionamiento. Cuando el fluido es un gas, en lugar de una bomba hay un compresor. Para poder funcionar, la bomba o el compresor requieren la entrada de una cierta cantidad de trabajo, Win. Este trabajo puede ser generado por la propia máquina o proceder de una fuente externa, como la red eléctrica.
- Una caldera, en la cual el agua pasa al estado de vapor, mediante la entrada de una cierta cantidad de calor, Qin. Cuando la fuente de calor es exterior a la propia caldera (como ocurre en una máquina de vapor típica, cuyo calor es proporcionado por una reacción nuclear -en las centrales nucleares- la luz solar -en las termosolares- o la combustión de carbón o gas -en las centrales térmicas-) se dice que tenemos una máquina de combustión externa. Cuando el calor es generado dentro de la propia cámara, como ocurre en los motores de los vehículos, se dice que la máquina es de combustión interna.
- La turbina es atravesada por el vapor que sale de la caldera y que es movido por la diferencia de presiones entre la entrada y la salida de la turbina. En su paso por la turbina, el vapor mueve los álabes de ésta, realizando un trabajo Wout que se puede aprovechar para generar electricidad. Una parte de este trabajo se emplea en hacer funcionar la bomba. Al realizar este trabajo, el vapor se enfría, de acuerdo con el primer principio de la termodinámica.
- Un condensador es una cámara en la que el vapor se pone en contacto con el ambiente, de forma que el vapor se condensa y vuelve a la forma de agua líquida. En este proceso se expulsa una cierta cantidad de desecho al ambiente, Qout. El agua vuelve a entrar en la bomba y se reanuda el ciclo.
En la figura tenemos el esquema de una central nuclear de agua a presión (PWR), en el que la máquina de vapor corresponde al ciclo secundario (en en el centro del esquema). En el ciclo, una bomba lleva el agua a un intercambiador de calor, que funciona como caldera, donde es evaporada mediante un aporte externo de calor. En el caso de la central nuclear, este calor proviene de una conducción de agua u otro fluido a muy altas temperaturas después de haber pasado por el reactor . El vapor que sale de la caldera se hace pasar por una turbina que mueve al generador eléctrico, el cual transmite la energía eléctrica la red. El vapor enfriado tras pasar por la turbina es enviado a un condensador, donde, en contacto con agua fría del exterior vuelve al estado líquido (por esto las centrales nucleares deben estar junto a ríos o junto al mar, como en el caso de Fukushima). Una vez licuado, el agua vuelve a entrar en la bomba, reiniciándose el proceso. La bomba es alimentada desde la red eléctrica, con lo cual a la producción de energía de la central hay que descontar lo que ella misma consume.
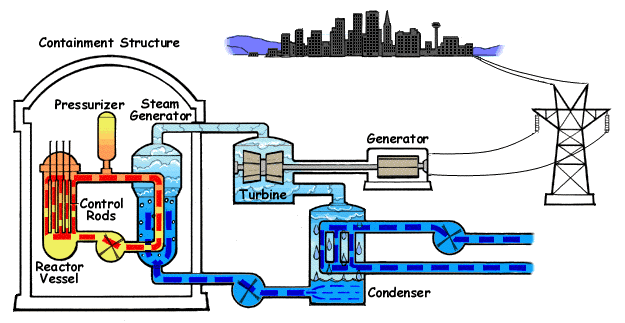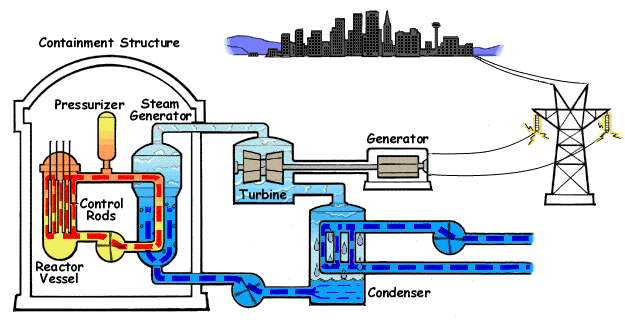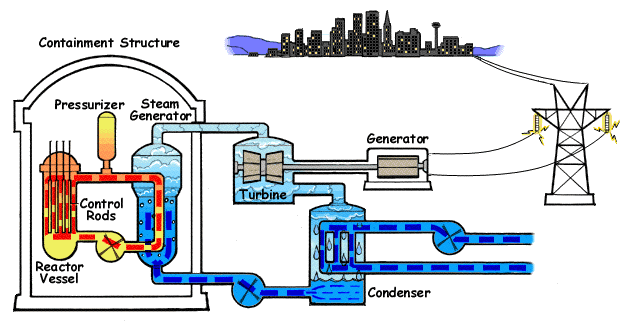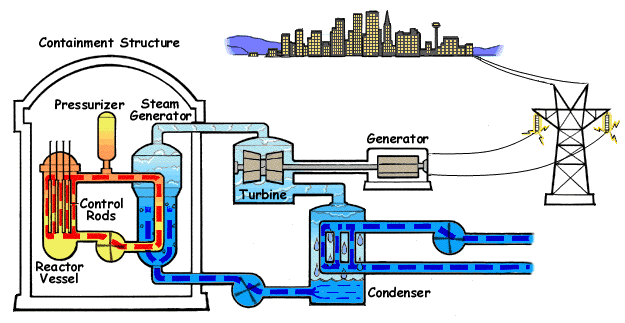
De acuerdo con el primer principio de la termodinámica, por tratarse de un proceso cíclico la energía interna del sistema no cambia en un ciclo, y el trabajo neto equivale a la diferencia entre el el calor que entra y el calor que sale
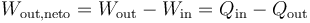
3 Rendimiento de una máquina térmica
Se define el rendimiento de una máquina térmica según el principio general de “lo que obtenemos dividido por lo que nos cuesta”. En este caso, “lo que obtenemos” es el trabajo neto que sale de la máquina. “Lo que nos cuesta” es el calor que entra procedente del reactor. Por tanto
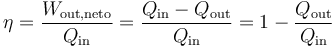
El funcionamiento de una máquina térmica real implica una serie de procesos que no son de equilibrio y que obligan a calcular el rendimiento principalmente de forma empírica.
4 Ciclos termodinámicos ideales
Para elaborar una teoría de una determinada máquina térmica, es necesario realizar una serie de simplificaciones y aproximaciones, de forma que el ciclo real se reduzca a procesos sencillos.
La principal de estas simplificaciones consiste en suponer que los procesos son cuasiestáticos de forma que el sistema se encuentra siempre muy próximo al equilibrio. De esta forma, el ciclo puede representarse en un diagrama de estado. El ciclo termodinámico de la máquina vendrá en ese caso representado por una curva cerrada. En el caso de un diagrama pV se tratará de una curva recorrida en sentido horario. El área delimitada por esta curva es el trabajo neto realizado en el ciclo, que será coincidente (en valor absoluto) con el calor neto que entra en el sistema.
El sustituir el proceso real por uno ideal es una aproximación que a menudo es muy mala, pero que posee la utilidad de funcionar como un referente, ya que en un proceso real el rendimiento es siempre inferior al de un ciclo ideal (por la presencia de rozamiento y otros factores disipativos). Por tanto, el ciclo ideal funciona como un límite al que aspirar. Si la teoría del ciclo ideal establece que el rendimiento máximo es de, por ejemplo, un 40%, sabemos que con un motor real nunca vamos a obtener más de esa cifra.
Dado que en la expresión del rendimiento aparece no el calor neto sino el que entra y el que sale, para el cálculo del rendimiento se hace preciso analizar cada uno de los tramos que componen el ciclo y no basta con el cálculo del área.
Consideremos un ciclo muy idealizado formado por cuatro procesos rectilíneos en un diagrama pV. Como punto de partida A tenemos 3 L a 100 kPa. Entonces se comprime a presión constante hasta un estado B de volumen 1 L. Fijando ahora el volumen se calienta hasta un estado C en el que su presión es de 400 kPa. Se expande ahora a presión constante hasta el estado D, en el que el volumen vuelve a ser de 3 L. por último se enfría a volumen constante hasta volver al estado A.
Este ciclo es una combinación de los dos procesos descritos en el ejemplo considerado en el Primer principio de la termodinámica, estando uno de ellos recorrido en sentido contrario.
Podemos aprovechar lo que allí se ve para tabular los calores y trabajos en cada proceso. Hay que cambiar el signo a los recorridos en sentido inverso a los de aquel ejemplo.
| W (J) | Q (J) | Q+W (J) | |
|---|---|---|---|
| A→B | +200 | −700 | −500 |
| B→C | 0 | +750 | +750 |
| C→D | −800 | +2800 | +2000 |
| D→A | 0 | −2250 | −2250 |
| A→B→C→D→A | −600 | +600 | 0 |
Esto nos da los calores de entrada y salida
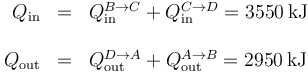
siendo el calor neto
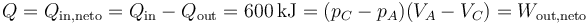
y el rendimiento

es decir que solo 1/6 del calor que entra se va en trabajo, y los restantes 5/6 se van en calor disipado al ambiente.
Este rendimiento está muy por debajo del que tendría una máquina de Carnot que operara entre las temperaturas extremas del ciclo. Este rendimiento máximo sería
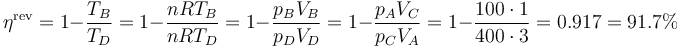
5 Ciclos más importantes
Entre los ciclos más importantes tenemos
- Ciclo Rankine, para máquinas de vapor.
- Ciclo Otto, que aproxima el comportamiento de los motores de explosión.
- Ciclo Diesel, para motores diésel.
- Ciclo Brayton (o Joule), que modela la conducta de una turbina de gas como las presentes en los motores de aviones o en las centrales de ciclo combinado.
Un ciclo ideal que sirve como referencia para el resto es el:
5.1 Ciclo de Carnot
Para conseguir la máxima eficiencia la máquina térmica reversible que necesitamos debe tomar calor de un foco caliente, cuya temperatura es como máximo Tc y verter el calor de desecho en el foco frío, situado como mínimo a una temperatura Tf.
Para que el ciclo sea óptimo, todo el calor absorbido debería tomarse a la temperatura máxima, y todo el calor de desecho, cederse a la temperatura mínima. Por ello, el ciclo que estamos buscando debe incluir dos procesos isotermos, uno de absorción de calor a Tc y uno de cesión a Tf.
Para conectar esas dos isotermas (esto es, para calentar el sistema antes de la absorción y enfriarlo antes de la cesión), debemos incluir procesos que no supongan un intercambio de calor con el exterior (ya que todo el intercambio se produce en los procesos isotermos). La forma más sencilla de conseguir esto es mediante dos procesos adiabáticos reversibles (no es la única forma, el motor de Stirling utiliza otro método, la recirculación). Por tanto, nuestra máquina térmica debe constar de cuatro pasos:
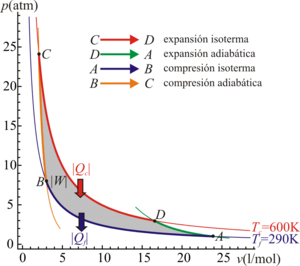
- C→D Absorción de calor Qin en un proceso isotermo a temperatura Tc.
- D→A Enfriamiento adiabático hasta la temperatura del foco frío, Tf.
- A→B Cesión de calor Qout al foco frío a temperatura Tf.
- B→C Calentamiento adiabático desde la temperatura del foco frío, Tf a la temperatura del foco caliente, Tc.
Aplicando este resultado al caso de un gas ideal, se llega a que el rendimiento de una máquina que operara según el ciclo de Carnot es
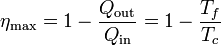
Para una máquina que trabaje entre 0°C y 100°C este rendimiento es del 26.8%. ¡Muy lejos del 100% ideal!
5.2 Ciclo Otto
En un motor de este tipo, en un cilindro se produce una compresión muy rápida de una mezcla de aire en el que se ha inyectado gasolina. Cuando el émbolo llega a su punto más alto, salta una chispa de una bujía que hace explotar la gasolina y empuja al pistón hacia abajo.
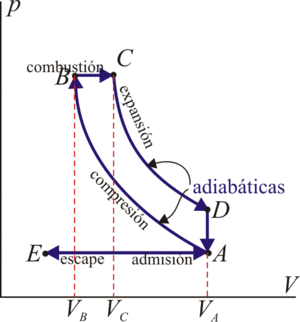
En el modelo matemático de este ciclo se supone que la compresión y la expansión son tan rápidas que a la mezcla no le da tiempo a intercambiar calor con el ambiente y por tanto son procesos adiabáticos. La explosión se modela como un calentamiento a volumen constante, ya que al estar el pistón en su punto más alto, su velocidad se anula justo en ese instante y el volumen cambia poco durante la explosión.
En el escape, los cases son expulsados de la cámara y sustituidos por mezcla nueva. realmente, se trata de un sistema abierto, pero se modela como si fuera el mismo aire que se ha enfriado cuando el émbolo estaba en su punto más bajo, lo que corresponde a otro procesos a volumen constante.
El ciclo Otto ideal, por tanto, está formado por dos adiabáticas y dos isócoras.
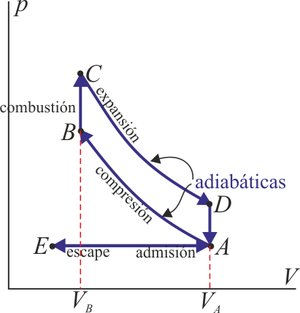
El rendimiento de este ciclo es igual a
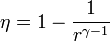
con γ = cp / cv = 1.4 y r = Vmax / Vmin la relación de compresión. Para un motor de automóvil típico, esta relación de compresión puede valer 8, lo que da un rendimiento del 56.5%.
5.3 Ciclo Diesel
Un ciclo Diésel ideal es un modelo simplificado de lo que ocurre en un motor diésel. En un motor de esta clase, a diferencia de lo que ocurre en un motor de gasolina la combustión no se produce por la ignición de una chispa en el interior de la cámara. En su lugar, aprovechando las propiedades químicas del gasóleo, el aire es comprimido hasta una temperatura superior a la de autoignición del gasóleo y el combustible es inyectado a presión en este aire caliente, produciéndose la combustión de la mezcla.
Puesto que sólo se comprime aire, la relación de compresión (cociente entre el volumen en el punto más bajo y el más alto del pistón) puede ser mucho más alta que la de un motor de gasolina (que tiene un límite, por ser indeseable la autoignición de la mezcla). La relación de compresión de un motor diésel puede oscilar entre 12 y 24, mientras que el de gasolina puede rondar un valor de 8.
En el modelo de un ciclo Diesel ideal, la única diferencia con el ciclo Otto ideal es que el calentamiento por la combustión no se produce a volumen constante, sino a presión constante. La razón es que en ese momento la cámara está abierta, puesto que se está inyectando el combustible, aunque su presión es por supuesto muy superior a la atmosférica.
El rendimiento de un ciclo Diesel ideal es
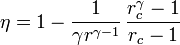
siendo r = VA / VB la razón de compresión y rc = VC / VB la relación de combustión.
Al tener una relación de compresión mayor, los motores diésel deben soportar presiones mucho mayores que los de gasolina (basados en el ciclo Otto). Por ello, son más pesados y robustos, lo que los encarece y limita su aplicabilidad a su uso en automóviles (aunque hoy día ya son de uso común). Por ello, tradicionalmente los motores diésel se han usado en sistemas donde su mayor peso no es determinante. En el sector del transporte se usan en barcos y trenes, y en la generación de energía se emplean en centrales de turbina de gas. Un motor diésel de un barco o central, puede ser gigantesco.


El más grande en la actualidad es el RT-flex96C, un motor diésel de dos tiempos montado en un buque.
5.4 Ciclo Brayton
El ciclo Brayton describe el comportamiento ideal de un motor de turbina de gas, como los utilizados en las aeronaves.

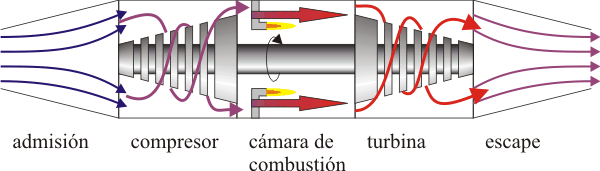
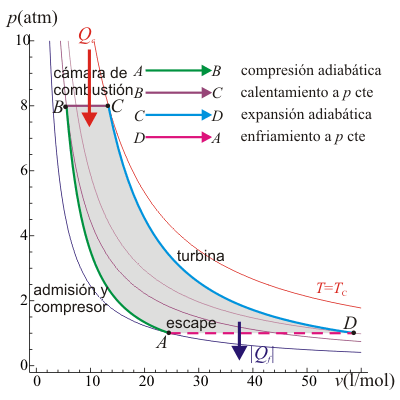
En este proceso se produce una admisión de aire frío desde el exterior Este aire es conducido hacia la cámara de combustión, donde se inyecta combustible, que calienta el aire de la cámara. Al expandirse, mueve la turbina y finalmente es expulsado al exterior. Dado que la compresión y la expansión son procesos muy rápidos, se modelan como adiabáticas, ya que el aire no tiene tiempo de intercambiar calor. La combustión, como en el caso del ciclo Diesel, se produce por inyección desde el exterior, lo que se modela como un proceso a presión constante.
En el escape, el aire enfriado (pero a una temperatura mayor que la inicial) sale al exterior, situado a la presión atmosférica, como el de la entrada. Técnicamente, este es un ciclo abierto ya que el aire que escapa no es el mismo que entra por la boca de la turbina, pero dado que sí entra en la misma cantidad y a la misma presión, se hace la aproximación de suponer una recirculación. En este modelo el aire de salida simplemente cede calor al ambiente y vuelve a entrar por la boca ya frío. En el diagrama pV esto corresponde a un enfriamiento a presión constante.
Existen de hecho motores de turbina de gas en los que el fluido efectivamente recircula y solo el calor es cedido al ambiente. Para estos motores, el modelo del ciclo de Brayton ideal es más aproximado que para los de ciclo abierto.
El rendimiento de un ciclo Brayton ideal es
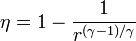
siendo r = pB / pA la relación de presión igual al cociente entre la presión al final del proceso de compresión y al inicio de él.
5.5 Ciclos de Stirling y Ericsson
5.5.1 Ciclo de Stirling
Un ciclo de Stirling es una versión idealizada de lo que ocurre en un motor de Stirling
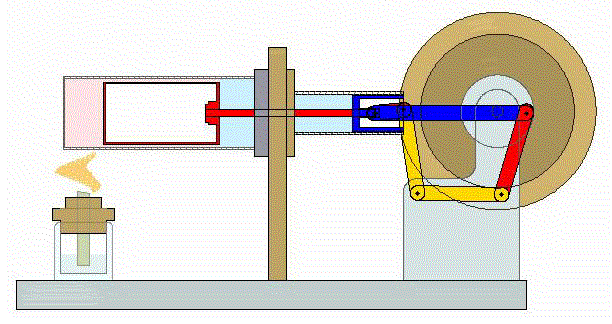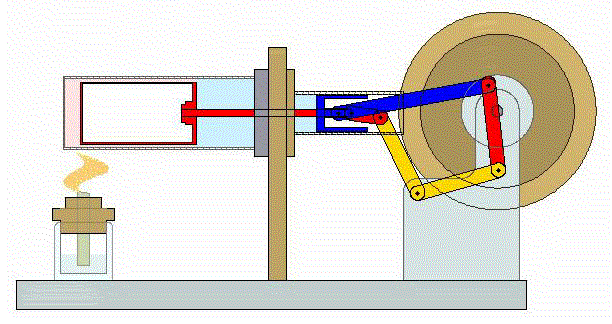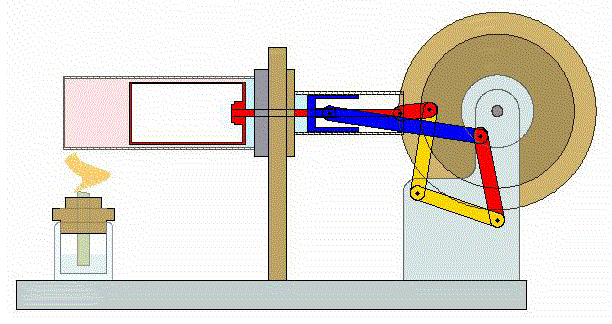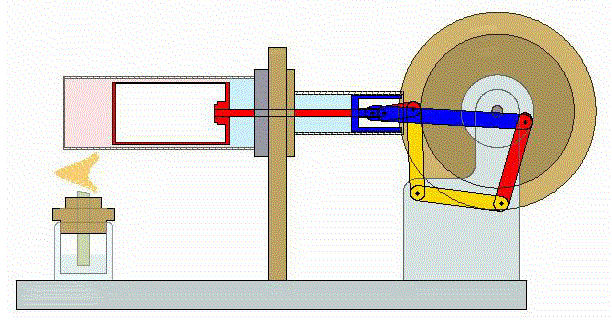
En su versión más simple, este ciclo está formado por cuatro pasos:
- A→B Se comprime el gas de forma isoterma. Esto corresponde a un tramo de hipérbola correspondiente a la temperatura indicada.
- B→C Se calienta el gas manteniendo fijado su volumen. Gráficamente, es una línea vertical entre las dos isotermas.
- C→D Se expande el gas a temperatura constante hasta que vuelve a su volumen inicial. Otro arco de hipérbola ahora recorrido hacia volúmenes crecientes.
- D→A Se enfría el gas manteniendo constante su volumen hasta que su temperatura vuelve a ser la inicial. Es un tramo vertical hacia abajo, cerrando el ciclo.
En este proceso se absorbe calor en el calentamiento a volumen constante y en la expansión isoterma, y se absorbe en los otros dos.
Un refinamiento del ciclo de Stirling es el siguiente. El calor que es liberado en el foco frío no puede reutilizarse para calentar el gas en el foco caliente, ya que ello supondría un flujo de calor del foco frío al caliente, lo que va en contra del segundo principio de la termodinámica. Sin embargo, no ocurre lo mismo con el gas liberado en el enfriamiento isócoro. En este caso, el gas pasa por todas las temperaturas entre digamos 1200 K y 300 K, cediendo calor gradualmente. En el calentamiento isócoro ocurre el proceso inverso: el gas pasa gradualmente desde los 300 K a los 1200 K, absorbiendo calor. En principio, el calor liberado en el enfriamiento puede reutilizarse en el calentamiento. El calor liberado cuando el gas pasa por 500 K en la bajada se entrega a otra cámara en la cual hay gas a 500 K en la subida. Puesto que las dos temperaturas son iguales, no se viola el segundo principio de la termodinámica. Este proceso se denomina regeneración y se consigue mediante un intercambiador de calor.
En un ciclo de Stirling con regeneración, todo el calor se absorbe a la temperatura del foco caliente, TC, y todo el calor se cede a la temperatura del foco frío, TF. Por ello, su rendimiento es el mismo que el de una máquina de Carnot que opere entre las temperaturas extremas
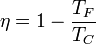
Un ciclo de Stirling real dista mucho de este modelo. Una medida de la evolución de la presión y la temperatura en un motor de Stirling produce figuras mucho más suavizadas en las que la forma del ciclo es aproximadamente elíptica.
En este problema se analiza un caso de ciclo de Stirling ideal.
5.5.2 Ciclo Ericsson
Un ciclo Ericsson es similar a uno de Stirling, con la diferencia de en lugar de dos isócoras, incluye un calentamiento y un enfriamiento a presión constantes, que en un diagrama pV son segmentos horizontales.
Como en el ciclo de Stirling, el ciclo Ericsson admite regeneración, de forma que el calor liberado en el enfriamiento se reutiliza en el calentamiento, de manera que el único calor absorbido se produce a la temperatura del foco caliente y el único calor cedido a la del foco frío. Si tiene regeneración, el rendimiento de un ciclo Ericsson ideal es también el mismo que el de una máquina de Carnot
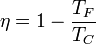

6 Máquinas reversibles
Una máquina reversible es una que puede operar en ambos sentidos, esto es, tanto como motor como como refrigerador. Esta máquina debe funcionar describiendo una serie de procesos cada uno de los cuales debe ser reversible (esto es, son procesos cuyo sentido de evolución se puede invertir mediante un cambio infinitesimal de las condiciones del entorno).
El concepto de máquina reversible, como el de proceso reversible, es una idealización. No existen máquinas reversibles en el mundo real, sino que deben considerarse como el límite al que tienden máquinas irreversibles cada vez más perfeccionadas.
El ejemplo más sencillo de máquina reversible es el de la máquina de Carnot, la cual opera según un ciclo de Carnot reversible. Cuando esta máquina se invierte se convierte en un refrigerador (o bomba de calor) de Carnot.
El rendimiento de una máquina reversible es
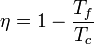
Cuando esta máquina funciona como refrigerador, su coeficiente de desempeño es
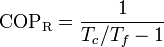
mientras que si actúa como bomba de calor será
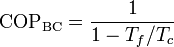
Entre los ciclos reversibles tenemos
- Ciclo de Carnot
- Ciclo de Stirling
- Ciclo Ericcson