Imán esférico
De Laplace
Contenido |
1 Enunciado
![]() Se dispone de una esfera de radio R con una imanación permanente
Se dispone de una esfera de radio R con una imanación permanente 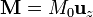 .
.
- Determine la expresión integral del potencial vector magnético. Calcule el valor de la integral. Hállese, a partir de
 , el valor de
, el valor de  y de
y de  en todos los puntos del espacio.
en todos los puntos del espacio.
- Describa cualitativamente la forma de
 ,
,  y
y 
- Calcule las corrientes de magnetización equivalentes, las ecuaciones y las condiciones de contorno para
 .
.
- Halle la distribución de cargas magnéticas equivalentes y el problema de ecuaciones y condiciones de contorno para
 .
.
2 Potencial vector
La expresión integral de  en términos de la magnetización es una generalización del potencial vector de un dipolo puntual,
en términos de la magnetización es una generalización del potencial vector de un dipolo puntual,
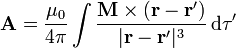
con la integral extendida a todo el espacio.
En nuestro caso, en que la magnetización es uniforme en la esfera y nula en el exterior, podemos extraer 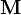 de la integral y escribir
de la integral y escribir
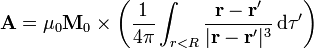
donde la integral se realiza únicamente en la esfera. Recordando, como en el problema de la esfera polarizada uniformemente, la integral que define el campo eléctrico creado por una distribución de carga
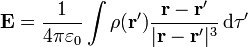
Vemos que la integral en cuestión es formalmente equivalente a la que da el campo eléctrico creado por una distribución
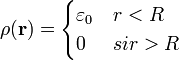
(esto no quiere decir que la integral sea un campo eléctrico, sólo que su forma es la misma). El campo que crearía esta distribución es conocido y vale
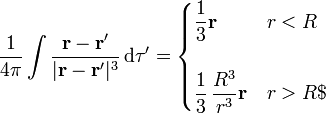
y, por tanto,
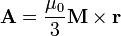
en el interior de la esfera y
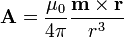
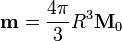
3 Forma de los campos
Una vez conocido el potencial vector, el cálculo del campo es inmediato. En particular, para el interior de la esfera resulta
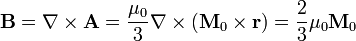
esto es, un campo uniforme en el mismo sentido que la magnetización.
En el exterior tenemos el potencial vector de un dipolo, correspondiente a que todo la magnetización estuviera concentrada en el centro de la esfera. El campo magnético correspondiente será asimismo uno dipolar
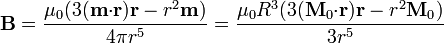
El campo magnético  , en el interior de la esfera, lo podemos obtener de la magnetización y del campo magnético
, en el interior de la esfera, lo podemos obtener de la magnetización y del campo magnético 
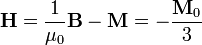
Resulta un valor uniforme, pero opuesto a la magnetización.
En el exterior, donde la magnetización es nula, el campo  es proporcional al campo magnético
es proporcional al campo magnético  ,
,
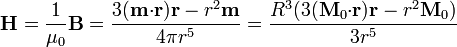
4 Corrientes de magnetización
Las corrientes de magnetización equivalentes están definidas como

![\mathbf{K}_m = \mathbf{n}\times[\mathbf{M}]](/wiki/images/math/f/7/e/f7e32e5788be56963bc508bf82ea6658.png)
La densidad de corriente de volumen es cero en el exterior de la esfera, en la cual la magnetización es nula. También lo es en el interior, ya que en él la magnetización es uniforme
\mathbf{J}_m = \cases{\nabla\times \mathbf{M}_0 = \mathbf{0} & $r<R$ \cr
\nabla\times\mathbf{0} = \mathbf{0} & $r> R$}
\]
\dibujops{cap7-10}Las corrientes superficiales no son nulas, ya que tenemos una
discontinuidad en la magnetización. Empleando coordenadas esféricas
\[
\mathbf{K}_m = \mathbf{n}\times[\mathbf{M}]=\mathbf{u}_{r}\times(\mathbf{0}-M_0\mathbf{u}_{z})=M_0\sen\theta\mathbf{u}_{\varphi}
\]
Estas corrientes rodean la esfera perpendicularmente a la
magnetización.
Dado que no hay corrientes libres, las ecuaciones para el campo magnético $\mathbf{B}$ son \[ \nabla{\cdot}\mathbf{B} = 0 \qquad \nabla\times \mathbf{B} = \mu_0(\mathbf{J}_l+\mathbf{J}_m) = \mathbf{0} \] \[ \mathbf{n}{\cdot}[\mathbf{B}]=0 \qquad \mathbf{n}\times[\mathbf{B}]=\mu_0(\mathbf{K}_l+\mathbf{K}_m) = \mu_0 M_0\sa\mathbf{u}_{\varphi} \] A partir de estas ecuaciones puede determinarse directamente el campo magnético, sin pasar por el potencial vector. El resultado, como hemos visto es que el campo magnético, de forma similar a lo que ocurre en una bobina recta, es uniforme en el interior y dipolar en el exterior, describiendo curvas cerradas en torno a las corrientes.





