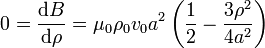Corriente en el interior de una tubería

De Laplace

Revisión a fecha de 20:00 25 mar 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución
- 2.1 Campo magnético
  - 2.1.1 Exterior del tubo
  - 2.1.2 Interior del tubo

1 Enunciado

Por el interior de una tubería cilíndrica de radio $a$ fluye un líquido con una velocidad, dependiente de la distancia al eje, $ρ$ , como

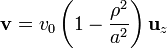
$\mathbf{v} = v_0\left(1-\frac{\rho^2}{a^2}\right)\mathbf{u}_{z}$

El líquido posee una densidad de carga uniforme $ρ 0$ , de forma que la densidad de corriente es 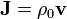$\mathbf{J} = \rho_0\mathbf{v}$ . En el exterior del tubo no hay corriente.

Halle el campo magnético que se produce tanto en el interior de la tubería como en el exterior de ella.
Calcule la fuerza que el campo magnético ejerce sobre una carga $q$ que se mueve con el líquido, a una distancia $a / 2$ del eje.

2 Solución

2.1 Campo magnético

El campo magnético en este sistema se calcula de forma análoga al caso de un hilo infinitamente largo y de un cable grueso.

Para este sistema, las leyes de la magnetostática nos dicen

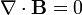
$\nabla\cdot\mathbf{B}=0$ $\nabla\times\mathbf{B}=\mu_0\mathbf{J}=\begin{cases}\mu_0J_0\mathbf{u}_z & (\rho<a) \\ \mathbf{0} & (\rho>a) \end{cases}$

Como en el caso del hilo delgado, podemos demostrar que

Las componentes del campo magnético no dependen de la coordenada $z$ (simetría traslacional).
Las componentes del campo magnético no dependen de la coordenada $\varphi$ (simetría acimutal).
La componente $B z$ , por ser el campo magnético ortogonal a la corriente que lo crea.
La componente $B ρ$ es nula, como consecuencia de la ley de Gauss para el campo magnético.

Por todo ello $\mathbf{B}$ se reduce a

$\mathbf{B}=B(\rho)\mathbf{u}_\varphi$

Aplicando ahora la ley de Ampère a un contorno circular concéntrico con el tubo de corriente, nos queda

$\oint \mathbf{B}\cdot\mathrm{d}\mathbf{r}=2\pi\rho\,B(\rho)=\mu_0 I(\rho) = \mu_0 \int\mathbf{J}\cdot\mathrm{d}\mathbf{S}$

siendo la corriente la que atraviesa una superficie apoyada en la circunferencia. Por comodidad tomaremos el círculo delimitado por ella, aunque cualquier otra valdría.

Tenemos dos casos:

2.1.1 Exterior del tubo

La corriente que atraviesa el círculo es toda la corriente que fluye por el tubo. Esta intensidad se calcula en el problema flujo de líquido por una tubería y el resultado es $I_T = 2\pi\rho_0v_0 \int_0^a \left(\rho-\frac{\rho^3}{a^2}\right)\,\mathrm{d}\rho = \frac{\pi\rho_0v_0a^2}{2}$

lo que nos da un campo magnético exterior

$\mathbf{B}=\frac{\mu_0\rho_0v_0a^2}{4\rho}\mathbf{u}_\varphi\qquad(\rho>a)$

2.1.2 Interior del tubo

En el interior del tubo, la corriente que atraviesa la superficie es la que corresponde a un círculo de radio

ρ

: $I(\rho) = \int_0^{2\pi}\!\!\!\mathrm{d}\varphi \int_0^\rho \mathrm{d}\rho\,\rho\,J(\rho)=2\pi\rho_0v_0 \int_0^\rho \left(\rho-\frac{\rho^3}{a^2}\right)\,\mathrm{d}\rho =2\pi\rho_0v_0\left(\frac{\rho^2}{2}-\frac{\rho^4}{4a^2}\right)$

y nos queda el campo magnético interior

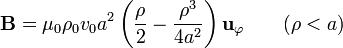
$\mathbf{B}=\mu_0\rho_0v_0a^2\left(\frac{\rho}{2}-\frac{\rho^3}{4a^2}\right)\mathbf{u}_\varphi\qquad(\rho<a)$

El valor máximo de este campo no se alcanza en la superficie, como en el caso del cable grueso, sino a una distancia dada por

$0 = \frac{\mathrm{d}B}{\mathrm{d}\rho}=\mu_0\rho_0v_0a^2\left(\frac{1}{2}-\frac{3\rho^2}{4a^2}\right)$ $\Rightarrow$ $\rho = \sqrt{\frac{2}{3}}a=0.817a$

Corriente en el interior de una tubería

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Campo magnético

2.1.1 Exterior del tubo

2.1.2 Interior del tubo

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES