Entrar Página Discusión Historial Go to the site toolbox

Problemas de cinemática de la partícula (CMR)

De Laplace

Contenido

1 Cálculo de velocidad media

Una partícula describe un movimiento rectilíneo tal que su velocidad instantánea cumple la ley

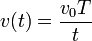
v(t) = \frac{v_0T}{t}

¿Cuánto vale la velocidad media entre 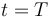t=T\, y t=3T\,?

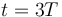2 Tiro parabólico sobre una pendiente

Se desea alcanzar un blanco que se encuentra sobre un plano inclinado un ángulo β, estando el blanco a una distancia D del punto de disparo.

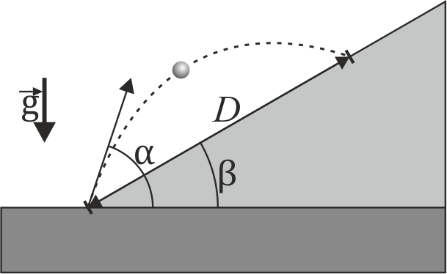
Archivo:parabola-pendiente.png
  1. ¿Cuál es la rapidez mínima que debe tener el proyectil para llegar al blanco? ¿Con qué ángulo sobre la horizontal debe dispararse en ese caso?
  2. Suponga que el plano tiene una pendiente del 75% y el proyectil se lanza con el ángulo que da el alcance máximo para llegar a D = 100 m. Para este caso, halle:
    1. La rapidez que tiene en el momento del impacto.
    2. La aceleración tangencial y normal (escalares) en el momento de impacto.

Tómese 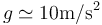g\simeq 10\mathrm{m}/\mathrm{s}^2.

3 Análisis de ecuación horaria

Una partícula se mueve por el espacio de forma que su velocidad, en las unidades fundamentales del SI, viene dada por la ecuación horaria

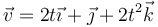
\vec{v}=2t\vec{\imath}+\vec{\jmath}+2t^2\vec{k}

Inicialmente la partícula se encuentra en 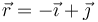\vec{r}=-\vec{\imath}+\vec{\jmath}.

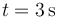  1. Calcule la posición en función del tiempo y el desplazamiento entre t=0\,\mathrm{s} y t=3\,\mathrm{s}. ¿Cuánto vale la velocidad media en dicho intervalo?
  2. Halle la rapidez en cada instante, así como la distancia que recorre la partícula en el mismo intervalo de tiempo. ¿Cuánto vale la rapidez media en este intervalo?
  3. Halle las componentes intrínsecas de la aceleración en t=1\,\mathrm{s}, como escalares y como vectores.
  4. Halle el triedro de Frenet en t=1\,\mathrm{s}.
  5. Calcule el radio de curvatura en t=1\,\mathrm{s} así como el centro de curvatura en ese instante.

4 Movimiento circular en 3D

Una partícula se mueve según las ecuaciones horarias

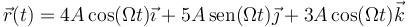
\vec{r}(t)=4A\cos(\Omega t)\vec{\imath}+ 5A\,\mathrm{sen}(\Omega t)\vec{\jmath}+3A\cos(\Omega t)\vec{k}

con A y Ω constantes.

  1. ¿Qué trayectoria sigue la partícula?
  2. ¿Qué desplazamiento realiza y qué distancia recorre la partícula entre t=0 y t = π/Ω?
  3. Justifique que este movimiento es circular y uniforme
  4. Determine la posición del centro del movimiento circular
  5. Calcule la velocidad angular de este movimiento circular

5 Ejemplo de movimiento helicoidal

El movimiento de un pájaro en una corriente térmica es aproximadamente helicoidal, compuesto de un movimiento ascensional y uno de giro alrededor del eje de subida, de forma que la velocidad en cada punto de la trayectoria puede escribirse como

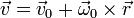
\vec{v}=\vec{v}_0+\vec{\omega}_0\times\vec{r}

siendo

\vec{v}_0 = v_0\vec{k}\qquad \vec{\omega}_0=\omega_0 \vec{k}

dos vectores constantes. Si la posición inicial es 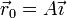\vec{r}_0=A\vec{\imath}

  1. Determine las ecuaciones horarias del movimiento. ¿Qué trayectoria describe?
  2. Halle los vectores tangente, normal y binormal para un instante arbitrario.
  3. Determine la aceleración tangencial, la normal y el radio de curvatura en cualquier instante.
  4. Calcule la distancia recorrida por la partícula en un intervalo de tiempo T=2π⁄ω_0

6 Movimiento cicloidal

Un punto exterior de una rueda que rueda sin deslizar describe una cicloide

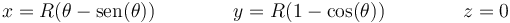
x=R(\theta-\mathrm{sen}⁡(\theta))\qquad\qquad y=R(1-\cos⁡(\theta))\qquad\qquad z=0
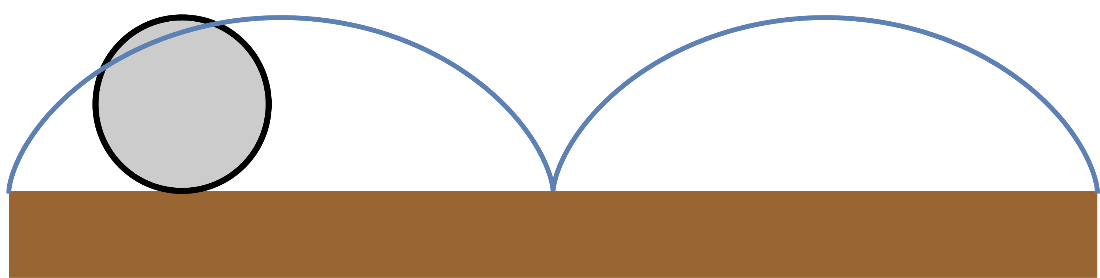
Archivo:movimiento-cicloidal.png
  1. Determine la velocidad y aceleración de la partícula en función de θ y sus derivadas respecto al tiempo. ¿Cuánto valen \vec{v} y \vec{a} en el momento en que el punto se halla en lo más alto de la rueda?
  2. Halle la aceleración tangente y normal.
  3. Calcule la posición de los centros de curvatura.
  4. Halle la distancia recorrida por el punto cuando la rueda da una vuelta completa.

7 Evolvente de una circunferencia

La evolvente de una circunferencia es la curva plana que se obtiene cuando se desenrolla un hilo tenso de un carrete circular. Suponga que se tiene una bobina de radio A que se va desenrollando de forma que el punto B donde el hilo deja de hacer contacto con el carrete forma un ángulo θ con el eje OX. Una partícula material se encuentra en el punto P situado en el extremo del hilo, moviéndose con este extremo a medida que el hilo se va desenrollando.

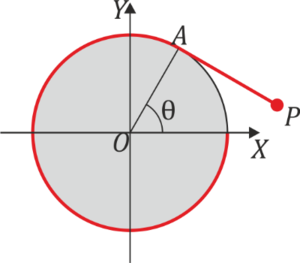
  1. Determine la ecuación de la trayectoria de P en función del parámetro θ.
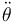  2. Exprese la velocidad y la aceleración de P en función de \theta\,, \dot{\theta} y \ddot{\theta}.
  3. ¿Cuál debe ser la ley horaria para que el movimiento sea uniforme?
  4. Para la ley horaria del apartado anterior, ¿cuánto valen la aceleración tangencial y la normal cuando θ = π2?

==Dos varillas articuladas Se tiene un sistema de dos varillas articuladas moviéndose en el plano OXY. Una de ellas, de longitud b tiene un extremo fijo O y gira en este plano con velocidad angular constante Ω respecto a unos ejes fijos. La segunda, de longitud b⁄2 se encuentra articulada a la primera en A y gira respecto a los ejes fijos con velocidad angular 2Ω. Para el punto P situado en el extremo de la segunda barra, calcule

  1. La ecuación horaria.
  2. Las componentes intrínsecas de la aceleración cuando Ωt vale 0, π/2, π.
  3. El radio y el centro de curvatura en los mismos instantes.
  4. La distancia total recorrida por P cuando la barra mayor da una vuelta completa.

8 Base vectorial en esféricas

Determine las expresiones para la velocidad y la aceleración en coordenadas esféricas {r,θ,φ}, como vectores en la base asociada a estas coordenadas 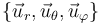\left\{\vec{u}_r,\vec{u}_\theta,\vec{u}_\varphi \right\}.

9 Dos varillas ortogonales

Una partícula P se encuentra en el extremo de dos varillas articuladas, describiendo un movimiento tridimensional. La primera varilla, de longitud b, tiene un extremo fijo en O y puede girar horizontalmente, formando un ángulo θ con el eje OX. La segunda varilla, de longitud h, se encuentra articulada en el extremo A de la primera y puede girar en un plano vertical, siendo siempre perpendicular a la primera varilla y formando un ángulo φ con el eje OZ.

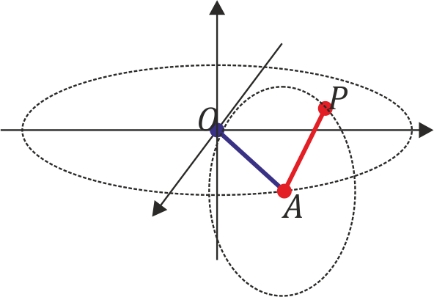
Archivo:dos-varillas-ortogonales.png
  1. ¿Sobre qué superficie puede moverse la partícula P?
  2. ¿Cómo es el movimiento si θ es constante y φ variable? ¿Y si φ es constante y θ variable?
  3. Exprese la posición, velocidad y la aceleración de P en términos de θ, φ y sus derivadas respecto al tiempo.

10 Movimiento sinusoidal cuadrático

Una partícula oscila según la ley

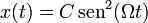
x(t) = C\,\mathrm{sen}^2(\Omega t)
  1. Pruebe que se trata de un movimiento armónico simple. ¿Cuál es su posición de equilibrio?
  2. ¿Cuánto valen la frecuencia, periodo y amplitud de este movimiento?

11 Estudio de un movimiento armónico simple

Un oscilador armónico con posición de equilibrio x = 0 se mueve de tal forma que en 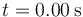t=0.00\,\mathrm{s} la partícula se halla en 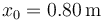x_0=0.80\,\mathrm{m}, moviéndose con velocidad 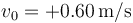v_0=+0.60\,\mathrm{m}/\mathrm{s} y aceleración 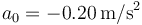a_0=-0.20\,\mathrm{m}/\mathrm{s}^2. Halle la frecuencia ω y el periodo del movimiento, su amplitud de oscilación y la fase inicial. Exprese los fasores (amplitudes complejas) de la posición, velocidad y aceleración.

12 Velocidad cuadrática con la posición

Una partícula se mueve a lo largo de una recta, de forma que su velocidad vale en cada punto v = − kx2. Su posición inicial es x(t = 0) = x0

  1. ¿Cuánto vale la aceleración de la partícula cuando se halla en un punto x?
  2. ¿Cuánto vale la posición como función del tiempo?

13 Caso de movimiento armónico simple

Una partícula describe el movimiento armónico simple de ecuación horaria, en el SI,

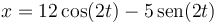
x = 12\cos(2t)-5\,\mathrm{sen}(2t)
  1. ¿Cuánto vale la amplitud de las oscilaciones? ¿Cuánto vale la fase inicial?
  2. Exprese los fasores de la posición, velocidad y aceleración para este movimiento.
Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_cinem%C3%A1tica_de_la_part%C3%ADcula_(CMR)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace