Contenido

1 Problemas del boletín

1 Problemas del boletín

1.1 Aro con deslizador

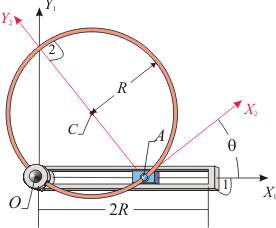
Sea un aro de centro $C$ y radio $R$ (sólido "2") que se mueve, en un plano fijo $O X 1 Y 1$ (sólido "1"), de tal modo que está obligado a deslizar en todo instante por un pasador giratorio situado en el punto $O$ , y además se halla articulado en su punto $A$ a un deslizador que se mueve siempre sobre el eje horizontal $O X 1$ (ver figura). Con carácter auxiliar, se define el sistema de ejes $O X 2 Y 2$ (sólido "2") solidario con el aro en su movimiento. Se pide:

Determinar gráfica y analíticamente la posición del C.I.R. del movimiento {21}.
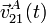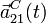Sabiendo que el ángulo $θ$ , que forman los ejes $O X 1$ y $A X 2$ , verifica la ley horaria $θ(t) = ω t$ (donde $ω$ es una constante conocida), calcular $\vec{v}_{21}^A(t)$ y $\vec{a}_{21}^C(t)$ .

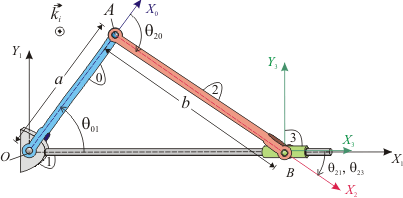
La figura muestra el mecanismo de biela-manivela. La manivela (sólido "0") gira alrededor del punto $O$ con velocidad angular uniforme $ω$ . La biela (sólido "2") gira alrededor de su punto de unión con la manivela (punto $A$ ). El otro extremo de la biela está unido (punto $B$ ) al deslizador (sólido "3") que realiza una traslación sobre el eje $X 1$

Utilizando el triángulo $O A B$ y la descomposición {31}={32}+{20}+{01}, verifica que el movimiento {31} es una traslación.

Determina gráficamente la posición de los C.I.R de todos los movimientos del problema.
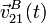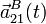Determina los vectores $\vec{v}^B_{21}(t)$ y $\vec{a}^B_{21}(t)$ .

1.2 Placa empujando un disco

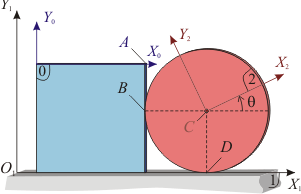
El cuadrado de la figura (sólido "0") realiza un movimiento plano cuando uno de sus lados desliza sobre un plano horizontal fijo (sólido "1"). El cuadrado empuja a un disco de radio $R$ (sólido "2") que rueda sin deslizar sobre el plano "1".

Determine la posición de los C.I.R. de los diferentes movimientos en el instante reflejado en la figura.
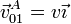Determine las reducciones cinemáticas de los movimientos en el instante en que la velocidad absoluta del punto $A$ del sólido "0" es $\vec{v}_{01}^A = v\vec{\imath}$ .
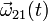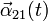Si el sistema parte del reposo y el punto $A$ del sólido "0" realiza un movimiento uniformemente acelerado, con aceleración $a 0$ , obtenga la expresión en función del tiempo del vector rotación $\vec{\omega}_{21}(t)$ y su derivada temporal $\vec{\alpha}_{21}(t)$ .
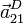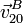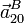En las condiciones del apartado anterior, calcule la expresión de la aceleración $\vec{a}_{21}^D$ , así como la velocidad y aceleración relativa $\vec{v}_{20}^B$ y $\vec{a}_{20}^B$ .

1.3 CIR de un velocípedo

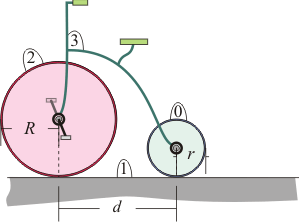
Los radios de las ruedas delantera (sólido "2") y trasera (sólido "0") de un velocípedo son $R$ y $r$ , respectivamente ( $R > r$ ); y los puntos de contacto de aquéllas con el suelo (sólido "1") están separados una distancia $d$ . Determinar gráficamente la posición del C.I.R. del movimiento {20}, sabiendo que las dos ruedas del velocípedo ruedan sin deslizar sobre el suelo.

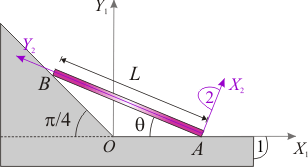
1.4 Movimiento de barra apoyada en planos no ortogonales

Una barra rígida (sólido “2”) de longitud

L

realiza un movimiento plano cuando sus extremos

A

y

B

deslizan, respectivamente, por un plano horizontal y otro inclinado (sólido “1”) que forman un ángulo

π / 4

.

Describa la reducción cinemática del movimiento {21} en términos del ángulo $θ$ y de su derivada temporal $\dot{\theta}$ , así como la posición del C.I.R.
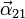Si el extremo $A$ realiza un movimiento rectilíneo uniforme con velocidad $v 0$ , obtenga el vector rotación $\vec{\omega}_{21}$ y su derivada temporal $\vec{\alpha}_{21}$ , en función de la posición de la barra.
En las condiciones del apartado anterior, obtenga la expresión de la velocidad y la aceleración del extremo $B$ .