Ejercicio de Movimiento Plano, Diciembre 2012 (F1 GIA)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Una barra rígida (sólido “2”) de longitud $L$ realiza un movimiento plano cuando sus extremos $A$ y $B$ deslizan, respectivamente, por un plano horizontal y otro inclinado (sólido “1”) que forman un ángulo $π / 4$ .

Describa la reducción cinemática del movimiento {21} en términos del ángulo $θ$ y de su derivada temporal $\dot{\theta}$ , así como la posición del C.I.R.
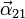Si el extremo $A$ realiza un movimiento rectilíneo uniforme con velocidad $v 0$ , obtenga el vector rotación $\vec{\omega}_{21}$ y su derivada temporal $\vec{\alpha}_{21}$ , en función de la posición de la barra.
En las condiciones del apartado anterior, obtenga la expresión de la velocidad y la aceleración del extremo $B$ .

2 Solución

2.1 Reducción cinemática del movimiento

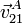El movimiento de la barra $\overline{AB}$ (sólido “2”), respecto de las superficies no ortogonales (sólido “1”) por las que deslizan los extremos de aquélla, quedá completamente caracterizado en cada instante por el vector rotación instantánea $\vec{\omega}_{21}$ , y la velocidad de un punto del sólido “2”; por ejemplo, la $\vec{v}_{21}^A$ del extremo $A$ de la barra:

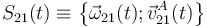
$S_{21}(t)\equiv\big\{\vec{\omega}_{21}(t)\mathrm{;}\!\ \vec{v}_{21}^A(t)\big\}$

Para determinar estos elementos definimos sendos sistemas de referencia asociados a cada uno de los sólidos: un $O X 1 Y 1 Z 1$ tal que el plano $O X 1 Z 1$ coincida con el plano horizontal del sólido “1”, tal como se indica en la figura. Para el sólido “2” definimos un sistema $A X 2 Y 2 Z 2$ tal que la propia barra $\overline{AB}$ coincida con el eje $A Y 2$ , y el eje $A Z 2$ sea en todo instante paralelo al $O X 1$ . Como consecuencia de esta elección, podemos obtener una condición sobre la dirección que ha de tener el vector rotación:

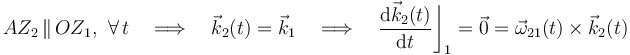
$AZ_2\!\ \|\!\ OZ_1\mathrm{,}\;\;\forall\,t \quad\Longrightarrow\quad \vec{k}_2(t)=\vec{k}_1\quad\Longrightarrow\quad\frac{\mathrm{d}\vec{k}_2(t)}{\mathrm{d}t}\bigg\rfloor_1=\vec{0}=\vec{\omega}_{21}(t)\times\vec{k}_2(t)$

Para que se verifique este resultado en todo instante debe ocurrir que, o bien el vector rotación es nulo, o es siempre paralelo al vector 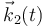$\vec{k}_2 (t)$ . La primera posibilidad ha de ser descartada, pues cuando la barra se mueve deslizando sus extremos $A$ y $B$ sobre los planos horizontal e inclinado, las velocidades de dichos puntos son estrictamente distintos. 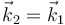En consecuencia, dicho vector va a tener en todo instante la dirección de los vecotores $\vec{k}_2=\vec{k}_1$ :

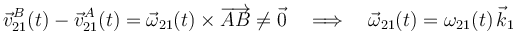
$\vec{v}_{21}^B(t)-\vec{v}_{21}^A(t)=\vec{\omega}_{21}(t)\times\overrightarrow{AB}\neq\vec{0}\quad\Longrightarrow\quad\vec{\omega}_{21}(t)=\omega_{21}(t)\!\ \vec{k}_1$

Por otra parte, la elección de ejes es tal que el extremo $A$ de la barra se desplace en todo momento a lo largo del eje $O X 1$ . Se tendrá, por tanto:

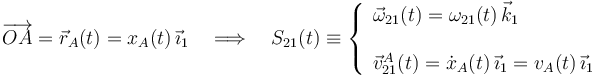
$\overrightarrow{OA}=\vec{r}_A(t)=x_A(t)\!\ \vec{\imath}_1\quad\Longrightarrow\quad S_{21}(t)\equiv\left\{\begin{array}{l}\vec{\omega}_{21}(t)=\omega_{21}(t)\!\ \vec{k}_1\\ \\ \vec{v}_{21}^A(t)=\dot{x}_A(t)\!\ \vec{\imath}_1=v_A(t)\!\ \vec{\imath}_1\end{array}\right.$

Nótese que esta reducción cinemática es características de un movimiento plano: en todo instante de tiempo el vector rotación instantánea tiene la misma dirección, a la cuál son siempre perpendiculares las velocidades instantáneas de todos los puntos del sólido:

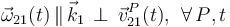
$\vec{\omega}_{21}(t)\!\ \|\!\ \vec{k}_1 \!\ \perp\!\ \vec{v}_{21}^P(t)\mathrm{,}\;\; \forall\,P\mathrm{,}\!\ t$

En el enunciado se pide determinar las magnitudes $ω 21$ y $v A$ en función de los valores de la varible geométrica $θ$ y de su derivada instantánea $\dot{\theta}$ . Para ello, aplicamos las propiedades del campo de velocidades del sólido rígido, que se sintetizan en el teorema de Chasles. Necesitamos, por tanto la expresión de la velocidad de otro punto de la barra, de la cuál conozcamos ciertas propiedades a priori. Esto ocurre con el extremo $B$ , que se desplaza siempre sobre el plano inclinado un ángulo $π / 4$ respecto de la horizontal, y siempre a distancia $L$ del extremo $A$ . Aplicando esta última propiedad, tenemos:

$\overrightarrow{AB}=\vec{r}_B(t)-\vec{r}_A(t)=L\!\ \bigg[-\cos\theta(t)\!\ \vec{\imath}_1+\mathrm{sen}\!\ \theta(t)\!\ \vec{\jmath}_1\!\ \bigg]\quad\Longrightarrow\quad\frac{\mathrm{d}\vec{r}_B(t)}{\mathrm{d}t}\bigg\rfloor_1-\!\ \frac{\mathrm{d}\vec{r}_A(t)}{\mathrm{d}t}\bigg\rfloor_1=\vec{v}_{21}^B(t)-\vec{v}_{21}^A(t)=L\!\ \dot{\theta}(t)\!\ \bigg[\mathrm{sen}\!\ \theta(t)\vec{\imath}_1+\cos\theta(t)\!\ \vec{\jmath}_1\!\ \bigg]$

donde hemos tenido en cuenta que las anteriores derivadas temporales son las definiciones de las velocidades instantáneas de los puntos $B$ y $A$ , respectivamente. Si aplicamos el teorema de Chasles para dichas velocidades, teniendo en cuenta la dirección conocida del vector rotación, se obtiene:

$\vec{v}_{21}^B(t)-\vec{v}_{21}^A(t)=\vec{\omega}_{21}(t)\times\overrightarrow{AB}=-L\!\ \omega_{21}(t) \!\ \bigg[\mathrm{sen}\!\ \theta(t)\vec{\imath}_1+\cos\theta(t)\!\ \vec{\jmath}_1\!\ \bigg]$

Identificando las dos expresiones obtenidas para la diferencia entre las velocidades de los puntos

B

y

A

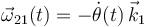
, determinamos la expresión del vector rotación en términos del valor de la derivada instantánea $\dot{\theta}$ : $\vec{\omega}_{21}(t)=-\dot{\theta}(t)\!\ \vec{k}_1$

Obsérvese que el signo ( $-$ ) que aparece en la expresión del vector rotación es clave para describir correctamente el movimiento del sólido “2”. 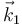Cuando el movimiento instantáneo de la barra es un giro en sentido antihorario, el ángulo $θ$ indicado en la figura disminuye su valor; en consecuencia, se tendrá que $\dot{\theta}$ es un número negativo y el vector $\vec{\omega}_{21}$ es estrictamente paralelo al vector $\vec{k}_1$ . Por el contrario, si la barra se mueve girando en sentido horario, el parámetro $θ$ crece en el tiempo y $\dot{\theta}$ será positivo. 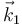En este caso, el vector rotación será antiparalelo al vector $\vec{k}_1$ , lo cual se corresponde con el sentido de giro propuesto.

Para obtener la expresión de la magnitud $v A$ , utilizaremos la propiedad del movimiento de $B$ , mencionada anteriormente: como este punto se desplaza siempre sobre el plano inclinado, la dirección de su velocidad está predeterminada:

$\vec{v}_{21}^B(t)=\frac{1}{\sqrt{2}}\!\ v_B(t)\!\ \bigg[\vec{\imath}_1\!\ -\!\ \vec{\jmath}_1\!\ \bigg]\quad\Longrightarrow\quad\vec{v}_{21}^B(t)\!\ -\!\ \vec{v}_{21}^A(t)=\bigg[\frac{v_B(t)}{\sqrt{2}}\!\ -\!\ v_A(t)\bigg]\!\ \vec{\imath}_1\!\ -\!\ \frac{v_B(t)}{\sqrt{2}}\!\ \vec{\jmath}_1$

Las componentes de este vector deben ser iguales a las de las anteriores expresiones obtenidas para la diferencia de velocidades; es decir:

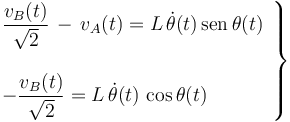
$\left.\begin{array}{l}\displaystyle \frac{v_B(t)}{\sqrt{2}}\!\ -\!\ v_A(t)=L\!\ \dot{\theta}(t)\!\ \mathrm{sen}\!\ \theta(t)\\ \\ \displaystyle-\frac{v_B(t)}{\sqrt{2}}=L\!\ \dot{\theta}(t)\!\ \cos\theta(t)\end{array}\right\}$ $\quad$ $\Rightarrow$ $\quad$ $\vec{v}_{21}^A(t)=-L\!\ \dot{\theta}(t)\!\ \bigg[\cos\theta(t)+\mathrm{sen}\!\ \theta(t)\bigg]\!\ \vec{\imath}_1$

2.1.1 Posición del C.I.R.

Una vez obtenidas las expresiones de los elementos de la reducción cinemática, podemos obtener la correspondiente posición del centro instantáneo de rotación (C.I.R.) del movimiento {21}, $I 21$ , mediante un procedimiento analítico. La posición relativa, respecto del centro de reducción $A$ , del punto geométrico $I = I 21$ , que coincide en un determinado instante con dicho C.I.R., viene dada por el segmento orientado:

$\overrightarrow{AI}(t)=\frac{\vec{\omega}_{21}(t)\times\vec{v}_{21}^A(t)}{|\vec{\omega}_{21}(t)|^2}=\frac{L\!\ \dot{\theta}^2(t)\!\ \big[\cos\theta(t)+\mathrm{sen}\!\ \theta(t)\big]\!\ \vec{k}_1\times\vec{\imath}_1}{\dot{\theta}^2(t)}$ $\quad$ $\Rightarrow$ $\quad$ $\overrightarrow{AI}(\theta)=L\!\ \big[\cos\theta+\mathrm{sen}\!\ \theta\big]\!\ \vec{\jmath}_1$

La consecuencia de este resultado es que, en todo instante de tiempo, la posición relativa del C.I.R.

I 21

, respecto de

A

, está determinada por el valor del parámetro

θ

, y no depende del valor de $\dot{\theta}$ . Es decir, la posición del C.I.R. depende de la posición de la barra (sólido “2”), pero no de cómo se mueve ésta.

Obsérvese que, tal como debe cumplirse necesariamente, la posición instantánea del C.I.R. $I 21$ coincide con el punto de intersección de las rectas $Δ A$ y $Δ B$ , contenidas en el plano director, que en cada instante pasan por los respectivos extremos $A$ y $B$ de la barra, y que son perpendiculares a la dirección de la velocidades del punto correspondiente:

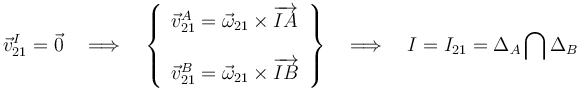
$\vec{v}_{21}^I=\vec{0}\quad\Longrightarrow\quad\left\{\begin{array}{l}\vec{v}_{21}^A=\vec{\omega}_{21}\times\overrightarrow{IA}\\ \\ \vec{v}_{21}^B=\vec{\omega}_{21}\times\overrightarrow{IB}\end{array}\right\}\quad\Longrightarrow\quad I=I_{21}=\Delta_A\bigcap\Delta_B$

donde $Δ A$ y $Δ B$ son tales que

$A\in\Delta_A\!\ \perp\!\ \vec{k}_1\mathrm{,}\!\ \vec{v}_{21}^A\mathrm{;}\qquad B\in\Delta_B\!\ \perp\!\ \vec{k}_1\mathrm{,}\!\ \vec{v}_{21}^B$

2.2 Caso de movimiento rectilíneo uniforme del extremo A

En el apartado anterior hemos obtenido la expresión general de la reducción cinemática, en términos de una ley horaria arbitraria $θ(t)$ y de su derivada instantánea 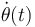$\dot{\theta}(t)$ . En éste y en el siguiente apartado se plantea un caso particular de movimiento de la barra, en el cuál, su extremo $A$ se desplaza a lo largo del eje $O X 1$ con un movimiento rectilíneo uniforme con velocidad constante de valor $v 0$ . Es decir,

$v_A(t)=-L\!\ \dot{\theta}(t)\!\ \bigg[\cos\theta(t)+\mathrm{sen}\!\ \theta(t)\bigg]=v_0\mathrm{,}\;\;\mathrm{cte.}\quad\Longrightarrow\quad \dot{\theta}(t)=\frac{\mathrm{d}\theta(t)}{\mathrm{d}t}=-\frac{v_0}{L\!\ \big[\cos\theta(t)+\mathrm{sen}\!\ \theta(t)\big]}$

Obsérvese que esta última expresión es la ecuación diferencial que, una vez integrada, con las condiciones iniciales pertinentes, proporciona la ley horaria $θ(t)$ . Aunque no se solicita dicha ley en el enunciado, puede calcularse de manera relativamente fácil: en la ecuación diferencial separamos en términos distintos los factores que dependen del ángulo $θ$ y del tiempo $t$ y procedemos a integrar cada uno de dichos términos:

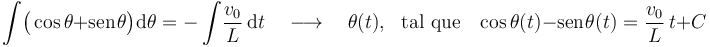
$\int\! \big(\cos\theta+\mathrm{sen}\!\ \theta\big)\!\ \mathrm{d}\theta=-\int\!\frac{v_0}{L}\ \mathrm{d}t \quad\longrightarrow\quad\theta(t)\mathrm{,}\;\;\;\mbox{tal que}\;\;\;\cos\theta(t)-\mathrm{sen}\!\ \theta(t)=\frac{v_0}{L}\ t+C$

El valor de la constante de integración $C$ depende de cúal fuese la posición en el instante inicial $t = 0$ . Por ejemplo, si consideramos que en dicho instante la barra se encuentra completamente apoyada en el plano inclinado -es decir, $θ(t = 0) = π / 4$ -, con su extremo $A$ situado en el origen $O$ , el valor de la constante es $C = 0$ .

Sin embargo, desde el punto de vista de las propiedades cinemáticas del movimiento de la barra, resulta mucho más interesante que podemos obtener una expresión de la reducción cinemática, estrictamente en términos de la posición de dicho sólido “2”, la cuál viene dada por el valor del ángulo $θ$ en cada instante:

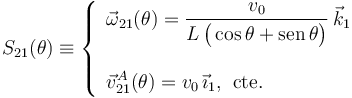
$S_{21}(\theta)\equiv\left\{\begin{array}{l}\displaystyle\vec{\omega}_{21}(\theta)=\frac{v_0}{L\!\ \big(\cos\theta+\mathrm{sen}\!\ \theta\big)}\!\ \vec{k}_1 \\ \\ \displaystyle\vec{v}_{21}^A(\theta)=v_0\!\ \vec{\imath}_1\mathrm{,}\;\;\mathrm{cte.}\end{array}\right.$

Y con la información que disponemos, también podemos calcular los valores de las derivadas instantáneas de los elementos de la reducción, en función de la posición de la barra. Comenzando por el vector rotación, se tendrá:

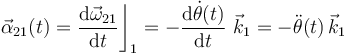
$\vec{\alpha}_{21}(t)=\frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\bigg\rfloor_1=-\frac{\mathrm{d}\dot{\theta}(t)}{\mathrm{d}t}\ \vec{k}_1=-\ddot{\theta}(t)\!\ \vec{k}_1$

Aplicando la regla de la cadena en la expresión $\dot{\theta}[\theta(t)]$ del comienzo de este apartado, se obtiene:

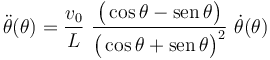
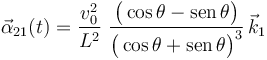
$\ddot{\theta}(\theta)=\frac{v_0}{L}\ \frac{\big(\cos\theta-\mathrm{sen}\!\ \theta\big)}{\big(\cos\theta+\mathrm{sen}\!\ \theta\big)^2}\ \dot{\theta}(\theta)$ $\Rightarrow$ $\vec{\alpha}_{21}(t)=\frac{v_0^2}{L^2}\ \frac{\big(\cos\theta-\mathrm{sen}\!\ \theta\big)}{\big(\cos\theta+\mathrm{sen}\!\ \theta\big)^3}\!\ \vec{k}_1$

Por otra parte, como el extremo $A$ realiza un movimiento rectilínea uniforme, su aceleración es nula en todo instante y para cualquier posición de la barra:

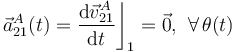
$\vec{a}_{21}^A(t)=\frac{\mathrm{d}\vec{v}_{21}^A}{\mathrm{d}t}\bigg\rfloor_1=\vec{0}\mathrm{,}\;\;\forall\,\theta(t)$

2.3 Movimiento del extremo B en las condiciones del apartado anterior

Una vez obtenida la reducción cinemática que describe el movimiento {21} en cualquier instante de tiempo, y las derivadas de sus elementos, tenemos determinado los campos de velocidades y aceleraciones de la barra cuando se mueve respecto del sólido fijo (sólido “1”). Así, la velocidad y aceleración instantáneas de cualquier punto $P$ del sólido “2”, han de ser:

$\begin{array}{l}\vec{v}_{21}^P(t)=\vec{v}_{21}^A(t)+\vec{\omega}_{21}(t)\times\overrightarrow{AP}\\ \\ \vec{a}_{21}^P(t)=\vec{a}_{21}^A(t)+\vec{\alpha}_{21}(t)\times\overrightarrow{AP}+\vec{\omega}_{21}(t)\times\bigg[\vec{\omega}_{21}(t)\times\overrightarrow{AP}\bigg]=\vec{a}_{21}^A(t)+\vec{\alpha}_{21}(t)\times\overrightarrow{AP}-|\vec{\omega}_{21}(t)|^2\ \overrightarrow{AP}\end{array}$

Para las condiciones del apartado anterior (movimiento rectilíneo uniforme del extremo $A$ de la barra), obtuvimos expresiones para los elementos de la reducción y sus derivadas, en términos de la posición de la barra dada por el parámetro $θ$ . La velocidad del extremo $B$ , en función de la posición se obtendría del siguiente cálculo:

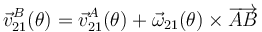
$\vec{v}_{21}^B(\theta)=\vec{v}_{21}^A(\theta)+\vec{\omega}_{21}( \theta)\times\overrightarrow{AB}$

Pero también podemos obtenerla a partir de la expresión general de la velocidad de dicho punto, que obtuvimos en el apartado 2.1:

$\vec{v}_{21}^B(t)=\frac{1}{\sqrt{2}}\!\ v_B(t)\!\ \bigg[\vec{\imath}_1\!\ -\!\ \vec{\jmath}_1\!\ \bigg]\mathrm{;}\quad\mbox{con}\quad v_B(t)=-\sqrt{2}\!\ L\!\ \dot{\theta}(t)\!\ \cos\theta(t)$

Sustituyendo la expresión de 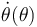$\dot{\theta}(\theta)$ obtenida en el apartado anterior...

$\vec{v}_{21}^B(\theta)=\frac{v_0\!\ \cos\theta}{\cos\theta+\mathrm{sen}\!\ \theta}\!\ \big[\vec{\imath}_1\!\ -\!\ \vec{\jmath}_1\!\ \big]$

Para calcular la aceleración intantánea del extremo $B$ , podríamos derivar con respecto al tiempo teniendo en cuenta que $θ = θ(t)$ y que conocemos el valor de $\dot{\theta}$ en cada instante o para cada posición de la barra. No obstante, apliquemos la expresión del campo de aceleraciones en este caso:

$\left.\begin{array}{l}\displaystyle \vec{a}_{21}^B(\theta)=\overbrace{\vec{a}_{21}^A(\theta)}^{=\vec{0}}+\vec{\alpha}_{21}(\theta)\times\overrightarrow{AB}-|\vec{\omega}_{21}(\theta)|^2\ \overrightarrow{AB}\\ \\ \displaystyle\overrightarrow{AB}=L\!\ \big[-\cos\theta\!\ \vec{\imath}_1+\mathrm{sen}\!\ \theta\!\ \vec{\jmath}_1\!\ \big]=L\!\ \vec{\jmath}_2(\theta)\end{array}\right\}\quad\Longrightarrow\quad \vec{a}_{21}^B(\theta)=- \frac{v_0^2}{L}\ \frac{\big(\cos\theta-\mathrm{sen}\!\ \theta\big)}{\big(\cos\theta+\mathrm{sen}\!\ \theta\big)^3}\ \vec{\imath}_2(\theta)\!\ -\!\ \frac{v_0^2}{L\!\ \big(\cos\theta+\mathrm{sen}\!\ \theta\big)^2}\ \vec{\jmath}_2(\theta)$

... Y teniendo en cuenta la expresión de los vectores unitarios del sistema de referencia ligado al sólido “2”, en términos función de los del sólido “1”, se obtiene:

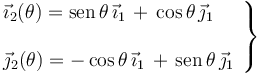
$\left.\begin{array}{l}\displaystyle \vec{\imath}_{2}(\theta)=\mathrm{sen}\!\ \theta\!\ \vec{\imath}_1\!\ + \!\ \cos\theta\!\ \vec{\jmath}_1\\ \\ \displaystyle\vec{\jmath}_{2}(\theta)=-\cos\theta \!\ \vec{\imath}_1\!\ + \!\ \mathrm{sen}\!\ \theta\!\ \vec{\jmath}_1 \end{array}\right\}$ $\Rightarrow$ $\vec{a}_{21}^B(\theta)=\frac{v_0^2}{L\!\ \big(\cos\theta+\mathrm{sen}\!\ \theta\big)^3}\ \big[\vec{\imath}_1\!\ - \!\ \vec{\jmath}_1\!\ \big]$

Ejercicio de Movimiento Plano, Diciembre 2012 (F1 GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Reducción cinemática del movimiento

2.1.1 Posición del C.I.R.

2.2 Caso de movimiento rectilíneo uniforme del extremo A

2.3 Movimiento del extremo B en las condiciones del apartado anterior

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES