Entrar Página Discusión Historial Go to the site toolbox

Problemas de cinemática del movimiento rectilíneo (GIE)

De Laplace

Contenido

1 Persecución policial

Las especificaciones del Seat Exeo establecen que va de 0 a 100 km/h en 9.2 s. ¿Cuánto vale su aceleración media en este periodo? ¿Cuánto vale el tiempo mínimo para atravesar un cruce de 15 m de anchura, si parte de estar parado en un semáforo? ¿Con qué velocidad llegaría al otro lado?

Un Seat León FR amarillo circula por la carretera a 160 km/h y pasa junto a un coche de la Guardia Civil parado en el arcén. Sabiendo que la benemérita usa un Seat Exeo, ¿cuál es el mínimo tiempo que tarda en alcanzar al Seat León si este no reduce su velocidad? ¿A qué distancia del punto donde estába parado lo alcanza? ¿Qué velocidad tiene el coche patrulla cuando alcanza al infractor?

2 Aproximación numérica de la velocidad y la aceleración

La posición de una partícula en distintos instantes de tiempo es, aproximadamente

t (s) 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
x (m) 0.00 -0.04 -0.06 -0.06 -0.04 0.00 0.06 0.14 0.24 0.36 0.50
  1. ¿En qué momento es máxima la velocidad? ¿En qué momento es nula? Calcule aproximadamente la velocidad en el intervalo entre t=0\,\mathrm{s} y t=1\,\mathrm{s}.
  2. Calcule aproximadamente la aceleración en el mismo intervalo.

3 Ejemplo de movimiento rectilíneo no uniforme

Una partícula se mueve a lo largo de una recta de forma que su posición sigue la ley, en el SI

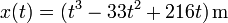
x(t) = (t^3-33t^2+216t)\,\mathrm{m}

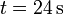entre t=0\,\mathrm{s} y t=24\,\mathrm{s}.

  1. Calcule la velocidad y la aceleración de este movimiento.
  2. ¿Cuál es la máxima distancia de la posición inicial a la que llega a encontrarse la partícula? ¿Cuánto vale el desplazamiento neto a lo largo del intervalo? ¿Y la distancia total recorrida?
  3. ¿Cuánto valen la máxima y la mínima rapidez de este movimiento?

4 Cálculo de velocidad media

Una partícula describe un movimiento rectilíneo tal que su velocidad instantánea cumple la ley

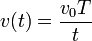
v(t) = \frac{v_0T}{t}

¿Cuánto vale la velocidad media entre t = T y t = 3T?

5 Ejemplos de velocidad en función de la posición

1) La velocidad de una partícula sigue la ley

v = \sqrt{Ax}

siendo x la distancia recorrida desde el instante inicial.

Calcule la aceleración de la partícula. ¿Qué tipo de movimiento describe?

2) Una partícula se mueve en línea recta, cumpliendo su velocidad instantánea

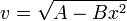
v = \sqrt{A- B x^2}

con A y B constantes positivas.

  1. ¿En que se medirá B en el SI?
  2. ¿Cómo depende de la posición la aceleración de la partícula?

6 Aceleración en un tramo rectilíneo

La longitud de la recta principal del circuito de Monza mide 1.3 km. Un Ferrari entra en la recta a 260 km/h y acelera durante 0.8 km hasta alcanzar 340 km/h. Mantiene esta velocidad hasta estar a 150 m de la primera chicane, a partir de ahí frena y llega la chicane a 80 km/h. Un Red Bull entra en la misma recta a 280 km/h, acelera hasta 320 km/h durante 0.5 km y frena al llegar a 120 m de la chicane, en la que entra a 90 km/h.

Suponiendo que las aceleraciones son constantes en cada uno de los tramos

  1. Determine las aceleraciones de los dos vehículos en cada uno de los tramos. Exprese los resultados como múltiplos de g.
  2. Calcule la velocidad media de cada uno. ¿Cuál tarda menos en recorrer la recta?
  3. Represente las gráficas de velocidad frente a la posición y frente al tiempo.

7 Ejemplo de integración numérica

Una partícula se mueve a lo largo de una recta, siendo su velocidad (en el SI) como función del tiempo, la dada por la gráfica

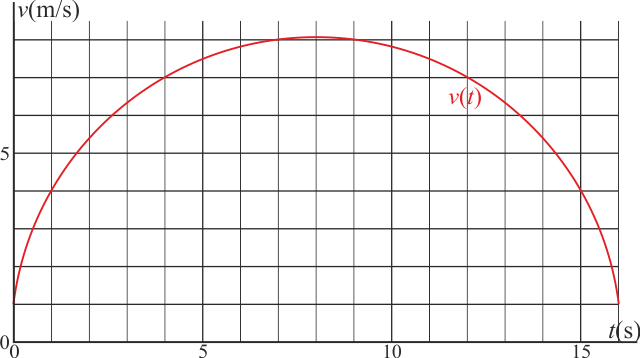
Archivo:velocidad-circulo.png

La partícula parte de s = 0.

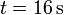  1. Aprovechando los puntos en que la curva cruza la cuadrícula, calcule aproximadamente la posición en que se encontrará la partícula en t=16\,\mathrm{s}.
  2. Calcule el valor exacto de esta posición, sabiendo que la ley para la velocidad es
v = \sqrt{1+16t-t^2}
¿Cuál es el error relativo cometido en el apartado anterior?

8 Calculo gráfico de velocidad media

La velocidad de una partícula en un movimiento rectilíneo sigue aproximadamente la gráfica de la figura cuando se representa frente al tiempo.

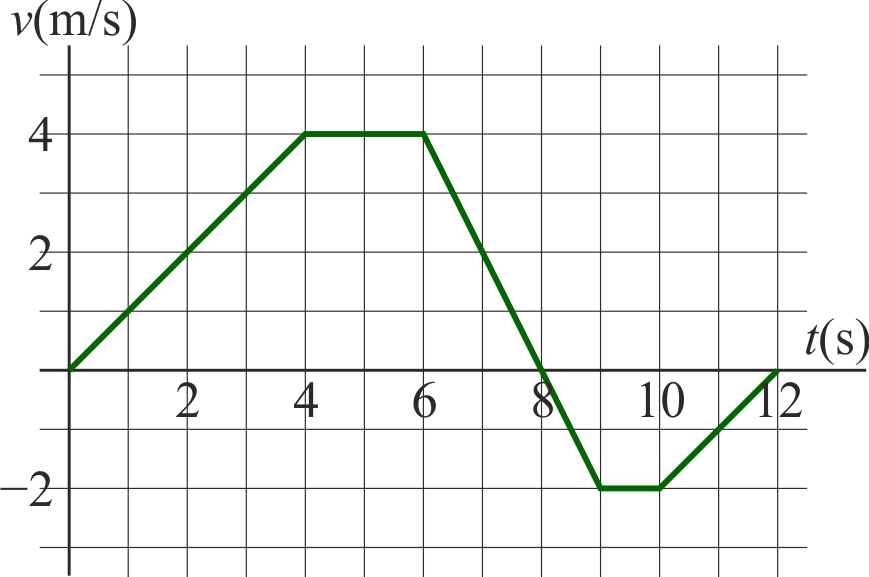
Archivo:velocidad-quebrada.png
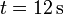  1. ¿Cuánto vale aproximadamente la velocidad media entre t=0\,\mathrm{s} y t=12\,\mathrm{s}?
  2. ¿Cuánto vale la distancia total recorrida por la partícula en el mismo intervalo?

9 Movimiento sinusoidal cuadrático

Una partícula oscila según la ley

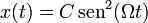
x(t) = C\,\mathrm{sen}^2(\Omega t)
  1. Pruebe que se trata de un movimiento armónico simple. ¿Cuál es su posición de equilibrio?
  2. ¿Cuánto valen la frecuencia, periodo y amplitud de este movimiento?
Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_cinem%C3%A1tica_del_movimiento_rectil%C3%ADneo_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace