Segundo principio de la termodinámica (GIE)
De Laplace
Contenido |
1 Introducción
El primer principio de la termodinámica establece que la energía interna puede aumentar porque se realice trabajo sobre el sistema o porque se introduzca calor en él. Desde este punto de vista calor y trabajo son equivalentes. Sin embargo, la experiencia diaria nos muestra que no es así, sino que existe una diferencia esencial entre ambos mecanismos de transferencia de energía. Podemos trasformar todo el trabajo en calor, pero no podemos transformar todo el calor en trabajo (si descendemos por una cuerda nos calentamos las manos, pero si nos calentamos las manos poniéndolas al sol, esto no nos hace subir la cuerda).
Igualmente, la experiencia nos muestra que existe una dirección en el que ocurren los fenómenos. Sabemos que el calor va de los cuerpos calientes a los fríos y no al revés; que un gas tiende a expandirse ocupando todo el volumen posible, y no a contraerse; que por consecuencia de la fricción los cuerpos se paran, no se aceleran.
Este sentido de evolución de los sistemas no está contenido en el primer principio de la termodinámica, sino que requiere un principio adicional, conocido como Segundo Principio de la Termodinámica.
2 Enunciado de Kelvin-Planck
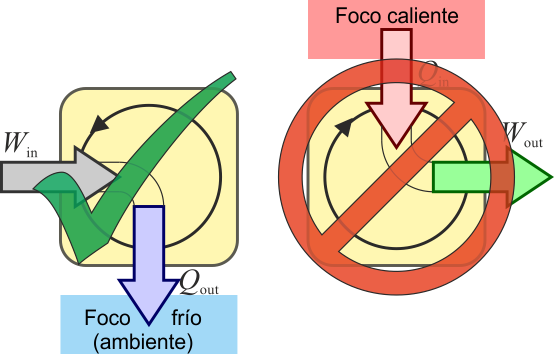
A la hora de aumentar la eficiencia de una máquina, el primer objetivo sería reducir, o eliminar si es posible, el calor de desecho Qout. Se plantean dos alternativas
- ¿Es posible una máquina térmica que no genere calor de desecho, sino que todo el calor absorbido se transforme en trabajo neto? Por ejemplo, podría usarse la turbina para enfriar directamente el vapor y reenviarlo al horno, sin pasar por un condensador donde se ceda calor al ambiente sin realizar trabajo útil
- ¿Es posible una reutilización del calor de desecho, de forma que se haga recircular y se incluya en el calor absorbido? La idea sería que el calor de derecho contribuya a calentar el vapor, en lugar de arrojarlo al exterior.
La respuesta a ambas preguntas es negativa.
El enunciado de Kelvin-Planck del Segundo Principio de la Termodinámica es el siguiente:
Es imposible construir una máquina que, operando en un ciclo, produzca como único efecto la extracción de calor de un foco y la realización de una cantidad equivalente de trabajo
Este enunciado refleja un hecho empírico y no se deduce de ninguna ley previa.
El enunciado de Kelvin-Planck afirma que es imposible construir una máquina que tenga un rendimiento del 100%. Siempre habrá calor de desecho que, en la mayoría de los casos equivale a más de la mitad del calor absorbido.
Es importante señalar que el enunciado de Kelvin-Planck habla de procesos cíclicos, que dejan al sistema en un estado final igual al inicial. Sí es posible transformar calor en trabajo si el estado final es diferente del inicial. Por ejemplo en una expansión isoterma de un gas, todo el calor que entra se transforma íntegramente en trabajo, pero al final el volumen del gas es diferente del inicial.
3 Procesos reversibles e irreversibles
El segundo principio establece a que existen procesos que pueden recorrerse en un sentido, pero no el opuesto. Podemos transformar íntegramente el trabajo en calor (es lo que hace una estufa de resistencias), pero no el calor en trabajo (ya que lo prohíbe el enunciado de Kelvin-Planck). Los ejemplos cotidianos abundan: si colocamos una taza de café caliente en el ambiente, el café se enfría, nunca se calienta más. Si vertemos azúcar en agua, no podemos invertir la disolución.
El Segundo Principio, por tanto, permite clasificar los procesos en reversibles e irreversibles.
- Proceso reversible
- es aquél cuyo sentido puede invertirse mediante un cambio infinitesimal de las condiciones del entorno.
- Proceso irreversible
- es el que no es reversible.
Por ejemplo, sea un sistema formado por un recipiente con agua en equilibrio térmico con hielo a 1 atm de presión. El sistema estará a 0.00°C.
Supongamos que el conjunto se encuentra rodeado por un baño térmico a +0.01°C. Sabemos que el hielo se irá derritiendo progresivamente, pasando a ser agua líquida. Si ahora cambiamos la temperatura exterior a -0.01°C, el hielo volverá a crecer, a costa de la congelación de agua. Hemos invertido el proceso mediante un cambio infinitesimal del entorno y el proceso es reversible.
Si en cambio el baño exterior está a 20.00°C sabemos que el hielo se derretirá. Si ahora pasamos la temperatura exterior a 19.99°C el hielo se seguirá derritiendo, por lo que no se invierte el proceso. Este proceso es irreversible.
Más en general, siempre que tengamos una diferencia finita de temperaturas entre un sistema y su entorno o entre diferentes partes de un sistema, tendremos un proceso irreversible.
Un razonamiento análogo se puede hacer analizando la expansión de un gas frente a una presión exterior. Si hay una diferencia finita de presiones es irreversible, si la diferencia es infinitesimal será reversible.
Todos los procesos reales son irreversibles, si bien existen procesos más o menos ideales, que se acercan a la reversibilidad. Los procesos reversibles permiten establecer además criterios de máximos o mínimos para los procesos reales. Por ejemplo, el máximo rendimiento de una máquina térmica se obtiene si esta opera reversiblemente.
Existen numerosas causas de irreversibilidad, mecánicas, térmicas, químicas,… A su vez, pueden ser externas o internas.
- Irreversibilidad interna
- es la que se produce dentro del sistema, debido a que este no se encuentra en equilibrio. Por ejemplo, al comprimir un gas bruscamente, el has próximo al pistón posee una presión mayor que los puntos alejados (produciéndose una onda de sonido). En este momento el gas no se encuentra en equilibrio (no existe la “presión del sistema”) y evoluciona de forma irreversible. Otro ejemplo sería la inmersión de un trozo de hielo en agua caliente, la diferencia finita de temperaturas entre partes de un sistema provoca irreversibilidad
- Irreversibilidad externa
- es aquella en la que quizás el sistema evoluciona reversiblemente, por ejemplo, porque su temperatura varía lentamente (como le ocurre a una taza de café caliente puesta en contacto con el exterior), pero aun así el proceso es irreversible porque la interacción con el entorno es irreversible (en el caso de la taza de café, porque existe una diferencia finita de temperaturas entre la café y el ambiente).
Así, tenemos:
- Irreversibilidad mecánica:
- Externa: Se deben a la transformación de trabajo en calor por la interacción del sistema con el entorno. El ejemplo más sencillo es la fricción. Consideremos el movimiento de ida y vuelta de un pistón en un cilindro, que roza tanto a la ida como a la vuelta. Es un proceso cíclico que transforma trabajo en calor. Su inversión significaría la transformación cíclica de calor en trabajo, lo que es imposible. Por ello, todo proceso mecánico que implique fricción (esto es, todos) es irreversible.
- Interna: Se debe a la conversión de trabajo en calor en el interior del sistema. Puede ser por fricción interna. Otro ejemplo es la expansión libre de un gas (el experimento de Joule). No hay trabajo ni intercambio de calor con el sistema, pero el proceso es irreversible.
- Irreversibilidad térmica:
- Externa: Se debe al intercambio de calor con el exterior de forma irreversible. El caso más importante es debido a una diferencia finita de temperaturas con el entorno. Su inversión implicaría que el calor debe pasar del cuerpo más frío al más caliente, lo que viola el enunciado de Clausius. Solo cuando es infinitesimal la diferencia de temperatura entre el sistema y su entorno puede producirse una transferencia reversible de calor.
- Interna: Debido a las transferencias de calor entre distintas partes de un mismo sistema.
- Otras irreversibilidades: Aparte de las mecánicas y térmicas tenemos irreversibilidades químicas (debidas a las reacciones espontáneas), de mezclas y disoluciones, la producción de calor por efecto Joule, etc.
Como vemos, son tantas las causas de irreversibilidad que es difícil imaginar un proceso reversible. Debe ser cuasiestático (para que el sistema esté siempre en equilibrio), sin fricción, manteniendo en todo momento la misma temperatura que el exterior, etc. Por ello los procesos reversibles son solo idealizaciones útiles.
4 Máquinas térmicas reversibles
Una máquina reversible es una que puede operar en ambos sentidos, esto es, tanto como motor como como refrigerador. Esta máquina debe funcionar describiendo una serie de procesos cada uno de los cuales debe ser reversible (esto es, son procesos cuyo sentido de evolución se puede invertir mediante un cambio infinitesimal de las condiciones del entorno).
El concepto de máquina reversible, como el de proceso reversible, es una idealización. No existen máquinas reversibles en el mundo real, sino que deben considerarse como el límite al que tienden máquinas irreversibles cada vez más perfeccionadas.
El ejemplo más sencillo de máquina reversible es el de la máquina de Carnot, la cual opera según un ciclo de Carnot reversible. Cuando esta máquina se invierte se convierte en un refrigerador (o bomba de calor) de Carnot.
5 Teorema de Carnot
El teorema de Carnot es un enunciado alternativo del Segundo Principio de la termodinámica, que se formula a partir de la comparación entre máquinas reversibles y máquinas irreversibles como:
El rendimiento de una máquina térmica M que opere entre dos focos no puede ser superior que el de una máquina reversible que opere entre los mismos focos
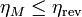
cumpliéndose la igualdad si la máquina M es también reversible y la desigualdad si es irreversible.
Puede demostrarse que el teorema de Carnot es equivalente al enunciado de Kelvin-Planck, aunque está formulado de una forma mucho más concreta que éste. El de Kelvin-Planck simplemente nos dice que no existe la máquina perfecta con rendimiento del 100%. El teorema de Carnot nos dice además que existe un máximo para ese rendimiento e incluso establece cómo hallar ese máximo. Basta con calcular el rendimiento de una máquina reversible que actúe entre las dos temperaturas indicadas.
Máquinas reversibles puede haber muchas con diferentes soportes (solo gas, agua y vapor, materiales magnéticos,…) por lo que puede resultar sorprendente que el rendimiento de todas ellas sea el mismo si trabajan entre las mismas temperaturas.
5.1 Aplicación a refrigeradores y bombas de calor
La aplicación del teorema de Carnot a un refrigerador establece que el COP máximo lo da un refrigerador que opere según un ciclo reversible, como el de Carnot. Este valor máximo es
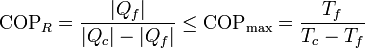
Para un frigorífico que mantiene los productos a 5°C en una habitación a 22°C este valor máximo es 16.4. Un frigorífico real posee un COP en torno a 4.
Para una bomba de calor, el COP máximo lo da también una bomba reversible, siendo su valor máximo
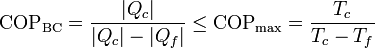
Una bomba de calor que mantiene una habitación a 22°C mientras el exterior está a 5°C tiene un coeficiente de desempeño máximo de 17.4 (uno más que para el frigorífico).
6 Enunciado de Clausius
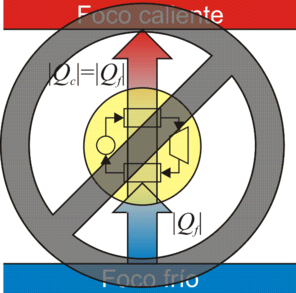
Es imposible un proceso que tenga como único resultado el paso de calor de un foco frío a un foco caliente
Como el enunciado de Kelvin-Planck, el enunciado de Clausius está formulado de manera negativa. Expresa un hecho empírico. En términos llanos, el enunciado de Clausius nos dice que para enfriar algo por debajo de la temperatura ambiente es necesario un trabajo adicional, esto es, que un frigorífico no funciona si no se enchufa
Puede demostrarse de forma sencilla que el enunciado de Clausius es equivalente al de Kelvin-Planck y al teorema de Carnot.
El enunciado de Clausius establece un sentido para la propagación del calor. Éste fluye de los cuerpos calientes a los fríos, nunca a la inversa. Por ello, una diferencia finita de temperaturas implica siempre una irreversibilidad, ya que su inversión violaría el enunciado de Clausius.
7 Equivalencia entre los enunciados
8 Temperatura Termodinámica
El cálculo del rendimiento de una máquina de Carnot que use gases ideales como fluido de trabajo se expresa en función de la temperatura absoluta medida con un termómetro como el de gas ideal a volumen constante. La expresión del rendimiento es por tanto dependiente de una propiedad termométrica concreta y es posible que para una máquina con un fluido de trabajo distinto el resultado fuera diferente.
Podemos evitar esta arbitrariedad empleando el propio teorema de Carnot. Si todas las máquinas reversibles poseen el mismo rendimiento, podemos medir la temperatura a partir del calor tomado o cedido por cualquiera de ellas, de acuerdo con la definición
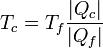
Lo único que se necesita es una temperatura de referencia, Tf, para la cual se toma la del punto triple del agua (273.16 K = 0.1°C).
Esta escala, que emplea el calor como propiedad termométrica, se denomina escala termodinámica de temperaturas. Posee la ventaja de que es fundamental, ya que se basa únicamente en leyes básicas de la física.
Por la forma en que se define la escala termodinámica resulta ser coincidente con la escala absoluta basada en un termómetro de gases ideales.