Equivalencia entre enunciados del Segundo Principio

De Laplace

1 Introducción

Puede demostrarse que los diferentes enunciados del Segundo Principio son equivalentes entre sí, es decir, que si cualquiera de ellos fuera falso, también lo serían los demás.

Recordemos algunos de los enunciados posibles del segundo principio de la termodinámica:

Enunciado de Kelvin Planck

Es imposible construir una máquina que, operando ciclicamente, produzca como único efecto la extracción de calor de un foco y la realización de una cantidad equivalente de trabajo

Enunciado de Clausius

Es imposible un proceso que tenga como resultado exclusivo la transferencia de calor de un foco frío a uno caliente

Teorema de Carnot

El rendimiento de una máquina térmica que opere entre dos temperaturas T_c y T_f es siempre menor que el de una máquina reversible que opere entre las mismas temperaturas

Como corolario al teorema de Carnot tenemos que el rendimiento de todas las máquinas reversibles que operen entre las mismas temperaturas es el mismo e igual al de una máquina de Carnot

Desigualdad de Clausius

Para cualquier procesos cíclico posible se verifica que

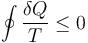
cumpliéndose la igualdad en el caso de un proceso reversible

Principio del aumento de entropía

En un proceso posible siempre se verifica que la entropía del universo aumenta

2 De Kelvin-Planck y de Clausius

Es fácil demostrar la equivalencia del enunciado de Kelvin Planck con el enunciado de Clausius:

Para demostrarlo debemos probar los dos sentidos de la demostración:

1. Si no se cumple el enunciado de Kelvin-Planck no se cumple el de Clausius

1. Si no se cumple el de Clausius no se cumple el de Kelvin-Planck

Para probar la primera proposición suponemos que no se verifica el enunciado de Kelvin-Planck, esto es que existe una máquina que transforma todo el calor | Q_c | que toma, en trabajo | W | = | Q_c | .

Si a la salida de esta máquina le conectamos un refrigerador que requiere para funcionar exactamente la misma cantidad de trabajo | W | y que toma una cantidad de calor | Q_f | del foco frío y coloca

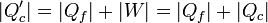
en el foco caliente, el resultado neto es un dispositivo que, sin realizar ni requerir trabajo (pues todo él es interno), toma una cantidad de calor | Q_f | del foco frío y la coloca en el foco caliente, lo que incumple el enunciado de Clausius.

Para probar la segunda afirmación suponemos un dispositivo que viola el enunciado de Clausius, esto es, que lleva una cierta cantidad de calor | Q_c | desde el foco frío al foco caliente.