Entrar Página Discusión Historial Go to the site toolbox

Máquinas térmicas (GIE)

De Laplace

Contenido

1 El primer principio en procesos cíclicos

El primer principio de la termodinámica establece que en todo sistema físico y para todo proceso

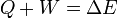
Q + W = \Delta E\,

siendo Q y W respectivamente el calor y el trabajo que entran en el sistema por su frontera y E la energía total del sistema, que incluye potencial, cinética y todo el resto que englobamos en el concepto de energía interna.

Un proceso cíclico es uno en el que el estado final es el mismo que el inicial, o que se repite periódicamente. Los procesos cíclicos son la base de todas las máquinas y motores, que operan de forma periódica. En un proceso cíclico la energía total al final del proceso es la misma que al principio, por tratarse de una función de estado. Por tanto

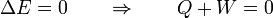
\Delta E = 0\qquad\Rightarrow\qquad Q + W = 0

Si desglosamos el calor y el trabajo entre lo que entra y lo que sale

Q = Q_\mathrm{in}-Q_\mathrm{out}\qquad\qquad W = W_\mathrm{in}-W_\mathrm{out}

nos queda

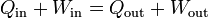
Q_\mathrm{in}+W_\mathrm{in} = Q_\mathrm{out}+W_\mathrm{out}\,

lo que nos dice que en un proceso cíclico lo que entra es igual a lo que sale.

No todos los términos son no nulos en todas las ocasiones.

En un motor eléctrico ideal, por ejemplo, en el sistema (el motor) entra trabajo eléctrico y sale trabajo mecánico, sin que haya calor implicado.

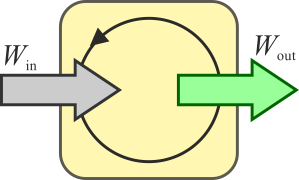
Archivo:motor-electrico-ideal.png

En un motor real, la situación anterior no es posible. Siempre hay factores que disipan energía en forma de calor como las resistencias eléctricas y el rozamiento. Esto provoca que no salga tanto trabajo como el que entra, y una parte se escapa en forma de calor disipado al ambiente. Para que fluya calor desde el sistema al ambiente, éste debe estar a una temperatura más baja que el sistema (lo que es lo habitual, ya que en los motores se alcanzan altas temperaturas). Por ello, el calor desechado va al “foco frío”.

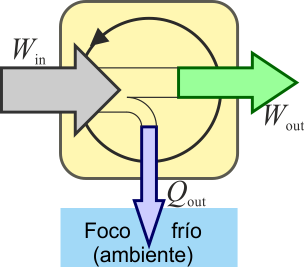
    Archivo:motor-electrico-02.jpg    Archivo:motor-electrico-real.png

Definimos entonces el rendimiento o eficiencia de una máquina, de manera general, como

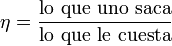
\eta = \frac{\mbox{lo que uno saca}}{\mbox{lo que le cuesta}}

que, en el caso de un motor eléctrico real sería

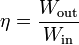
\eta = \frac{W_\mathrm{out}}{W_\mathrm{in}}

En una estufa de resistencia, en cambio, todo el trabajo que entra sale en forma de calor.

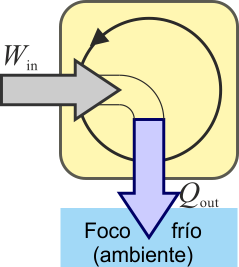
Archivo:estufa-electrica.jpg    Archivo:maquina-estufa.png

El rendimiento de esta estufa sería

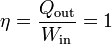
\eta = \frac{Q_\mathrm{out}}{W_\mathrm{in}}=1

2 Máquina térmica

El mismo principio anterior se puede aplicar a un dispositibvo que transforma calor en trabajo. ]Una máquina térmica es un dispositivo que, operando de forma cíclica, toma de calor de un foco caliente, realiza un cierto trabajo (parte del cual se emplea en hacer funcionar la propia máquina) y entrega calor de desecho a un foco frío, normalmente el ambiente.

Imagen:maquina-termica-02.png

2.1 Máquina de vapor

El ejemplo característico de máquina térmica es la máquina de vapor, que se emplea en la mayoría de las centrales eléctricas (sean estas térmicas, termo-solares o nucleares).

En la figura tenemos el esquema de una central nuclear, en el que la máquina de vapor corresponde al ciclo etiquetado como “19”. En el ciclo, un compresor (21) se encarga de enviar agua fría a alta presión hasta una caldera (6), donde es evaporada mediante un aporte externo de calor. En el caso de la central nuclear, este calor proviene de una conducción de agua u otro fluido a muy altas temperaturas después de haber pasado por el reactor (7). El vapor que sale de la caldera se hace pasar por una turbina que mueve al generador eléctrico (9), el cual transmite la energía eléctrica la red. Una segunda turbina (8) se encarga de mover el compresor, de manera que el ciclo se mantiene en funcionamiento usando parte de la energía generada. El vapor enfriado tras pasar por la turbina es enviado a un condensador, donde, en contacto con agua fría del exterior vuelve al estado líquido (por esto las centrales nucleares deben estar junto a ríos o junto al mar, como en el caso de Fukushima). Una vez licuado, el agua vuelve a entrar en el compresor, reiniciándose el proceso.

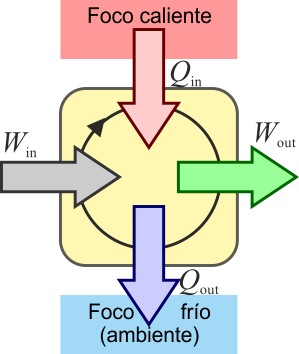
Tenemos cuatro términos energéticos en este proceso:

  • El calor Qin proporcionado por el foco caliente, en este caso el agua proveniente del reactor.
  • El calor Qout cedido al foco frío, que en este caso es el agua de ríos y mares, más lo que se arroja a la atmósfera como vapor (20)
  • El trabajo Wout realizado por la turbina que mueve al generador eléctrico
  • El trabajo Win necesario para hacer funcionar la propia máquina

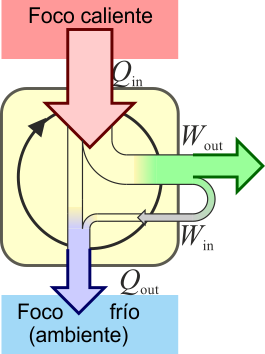
De acuerdo con el primer principio de la termodinámica, por tratarse de un proceso cíclico la energía interna del sistema no cambia en un ciclo, y el trabajo neto equivale a la diferencia entre el el calor que entra y el calor que sale

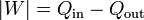
|W| = Q_\mathrm{in}-Q_\mathrm{out}\,

3 Rendimiento de una máquina térmica

Se define el rendimiento de una máquina térmica según el principio general de “lo que obtenemos dividido por lo que nos cuesta”. En este caso, “lo que obtenemos” es el trabajo neto. “Lo que nos cuesta” es el calor que entra procedente del reactor. Por tanto

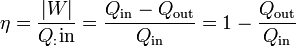
\eta = \frac{|W|}{Q_:\mathrm{in}} = \frac{Q_\mathrm{in}-Q_\mathrm{out}}{Q_\mathrm{in}} = 1 - \frac{Q_\mathrm{out}}{Q_\mathrm{in}}

El funcionamiento de una máquina térmica real implica una serie de procesos que no son de equilibrio y que obligan a calcular el rendimiento principalmente de forma empírica.

4 Ciclos termodinámicos ideales

Para elaborar una teoría de una determinada máquina térmica, es necesario realizar una serie de simplificaciones y aproximaciones, de forma que el ciclo real se reduzca a procesos sencillos.

La principal de estas simplificaciones consiste en suponer que los procesos son cuasiestáticos de forma que el sistema se encuentra siempre muy próximo al equilibrio. De esta forma, el ciclo puede representarse en un diagrama de estado. El ciclo termodinámico de la máquina vendrá en ese caso representado por una curva cerrada. En el caso de un diagrama pV se tratará de una curva recorrida en sentido horario. El área delimitada por esta curva es el trabajo neto realizado en el ciclo, que será coincidente (en valor absoluto) con el calor neto que entra en el sistema.

El sustituir el proceso real por uno ideal es una aproximación que a menudo es muy mala, pero que posee la utilidad de funcionar como un referente, ya que en un proceso real el rendimiento es siempre inferior al de un ciclo ideal (por la presencia de rozamiento y otros factores disipativos). Por tanto, el ciclo ideal funciona como un límite al que aspirar. Si la teoría del ciclo ideal establece que el rendimiento máximo es de, por ejemplo, un 40%, sabemos que con un motor real nunca vamos a obtener más de esa cifra.

Dado que en la expresión del rendimiento aparece no el calor neto sino el que entra y el que sale, para el cálculo del rendimiento se hace preciso analizar cada uno de los tramos que componen el ciclo y no basta con el cálculo del área.

Así, por ejemplo, en el caso del ciclo rectangular de la figura:

  • El proceso A→B es un enfriamiento a presión constante. En él el calor sale del sistema, según la ley
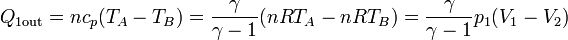
Q_{1\mathrm{out}} = nc_p(T_A-T_B) = \frac{\gamma}{\gamma-1}(nRT_A-nRT_B) = \frac{\gamma}{\gamma-1}p_1(V_1-V_2)
  • El proceso B→C es un calentamiento a volumen constante. En él el calor entra en el gas, con el valor
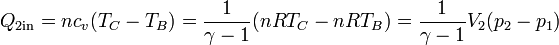
Q_{2\mathrm{in}} = nc_v(T_C-T_B) = \frac{1}{\gamma-1}(nRT_C-nRT_B) = \frac{1}{\gamma-1}V_2(p_2-p_1)
  • El proceso C→D es también de calentamiento, pero ahora a presión constante. En él el calor entra en el sistema,
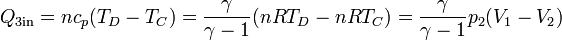
Q_{3\mathrm{in}} = nc_p(T_D-T_C) = \frac{\gamma}{\gamma-1}(nRT_D-nRT_C) = \frac{\gamma}{\gamma-1}p_2(V_1-V_2)
  • Por último, el paso D→A es de enfriamiento a volumen constante.
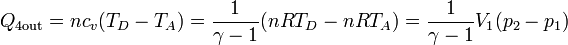
Q_{4\mathrm{out}} = nc_v(T_D-T_A) = \frac{1}{\gamma-1}(nRT_D-nRT_A) = \frac{1}{\gamma-1}V_1(p_2-p_1)

Esto nos da los calores de entrada y salida

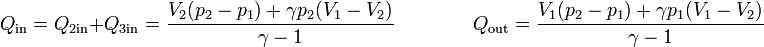
Q_\mathrm{in}=Q_{2\mathrm{in}}+Q_{3\mathrm{in}} = \frac{V_2(p_2-p_1)+\gamma p_2(V_1-V_2)}{\gamma-1}\qquad\qquad Q_\mathrm{out} = \frac{V_1(p_2-p_1)+\gamma p_1(V_1-V_2)}{\gamma-1}

siendo el calor neto

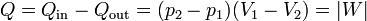
Q=Q_\mathrm{in}-Q_\mathrm{out}= (p_2-p_1)(V_1-V_2) = |W|\,

y el rendimiento

\eta = \frac{|W|}{Q_\mathrm{in}}=\frac{(\gamma-1)(p_2-p_1)(V_1-V_2)}{V_2(p_2-p_1)+\gamma p_2(V_1-V_2)}

La expresión es complicada ya que aunque este ciclo posee una expresión muy sencilla desde el punto de vista del trabajo, no lo es tanto desde el calor, ya que hay intercambios en los cuatro pasos. Si, siguiendo este ejemplo, consideramos que inicialmente tenemos 1 m³ de aire (γ = 1.4) a 100 kPa que se comprime hasta ocupar 0.25 m³ y luego se aumenta su presión hasta 300 kPa, resulta un rendimiento

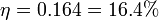
\eta = 0.164 = 16.4\%

es decir que solo 1/6 del calor que entra se va en trabajo, y los restantes 5/6 se van en calor disipado al ambiente.

5 Ciclos termodinámicos

Entre los ciclos más importantes tenemos

Un ciclo ideal que sirve como referencia para el resto es el:

5.1 Ciclo de Carnot

Artículo completo: Ciclo de Carnot (GIE)

Para conseguir la máxima eficiencia la máquina térmica reversible que necesitamos debe tomar calor de un foco caliente, cuya temperatura es como máximo Tc y verter el calor de desecho en el foco frío, situado como mínimo a una temperatura Tf.

Para que el ciclo sea óptimo, todo el calor absorbido debería tomarse a la temperatura máxima, y todo el calor de desecho, cederse a la temperatura mínima. Por ello, el ciclo que estamos buscando debe incluir dos procesos isotermos, uno de absorción de calor a Tc y uno de cesión a Tf.

Para conectar esas dos isotermas (esto es, para calentar el sistema antes de la absorción y enfriarlo antes de la cesión), debemos incluir procesos que no supongan un intercambio de calor con el exterior (ya que todo el intercambio se produce en los procesos isotermos). La forma más sencilla de conseguir esto es mediante dos procesos adiabáticos reversibles (no es la única forma, el motor de Stirling utiliza otro método, la recirculación). Por tanto, nuestra máquina térmica debe constar de cuatro pasos:

  • C→D Absorción de calor Qc en un proceso isotermo a temperatura Tc.
  • D→A Enfriamiento adiabático hasta la temperatura del foco frío, Tf.
  • A→B Cesión de calor | Qf | al foco frío a temperatura Tf.
  • B→C Calentamiento adiabático desde la temperatura del foco frío, Tf a la temperatura del foco caliente, Tc.

Aplicando este resultado al caso de un gas ideal, se llega a que el rendimiento máximo de una máquina térmica es

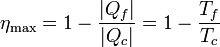
\eta_\mathrm{max} = 1 - \frac{|Q_f|}{|Q_c|}=1 - \frac{T_f}{T_c}

Para una máquina que trabaje entre 0°C y 100°C este rendimiento máximo es del 26.8%. ¡Muy lejos del 100% ideal!

5.2 Ciclo Otto

Artículo completo: Ciclo Otto (GIE)

5.3 Ciclo Diesel

Artículo completo: Ciclo Diesel (GIE)

5.4 Ciclo Brayton

Artículo completo: Ciclo Brayton (GIE)

5.5 Ciclos de Stirling y Ericsson

6 Máquinas reversibles

Una máquina reversible es una que puede operar en ambos sentidos, esto es, tanto como motor como como refrigerador. Esta máquina debe funcionar describiendo una serie de procesos cada uno de los cuales debe ser reversible (esto es, son procesos cuyo sentido de evolución se puede invertir mediante un cambio infinitesimal de las condiciones del entorno).

El concepto de máquina reversible, como el de proceso reversible, es una idealización. No existen máquinas reversibles en el mundo real, sino que deben considerarse como el límite al que tienden máquinas irreversibles cada vez más perfeccionadas.

El ejemplo más sencillo de máquina reversible es el de la máquina de Carnot, la cual opera según un ciclo de Carnot reversible. Cuando esta máquina se invierte se convierte en un refrigerador (o bomba de calor) de Carnot.

El rendimiento de una máquina reversible es

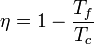
\eta = 1- \frac{T_f}{T_c}

Cuando esta máquina funciona como refrigerador, su coeficiente de desempeño es

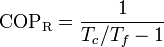
\mathrm{COP}_\mathrm{R}=\frac{1}{T_c/T_f-1}

mientras que si actúa como bomba de calor será

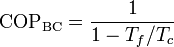
\mathrm{COP}_\mathrm{BC}=\frac{1}{1-T_f/T_c}

Entre los ciclos reversibles tenemos

Obtenido de "http://tesla.us.es/wiki/index.php/M%C3%A1quinas_t%C3%A9rmicas_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace