Problemas de Dinámica del punto (GIC)

De Laplace

1 Equilibrio de una partícula bajo la acción de tres muelles

Una partícula libre de masa m está unida a tres muelles de longitud natural nula y constantes elásticas k_A, k_B y k_C. Cada uno de los muelle tiene el otro extremo fijado en un punto. Las coordenadas de los puntos de fijación son A( − a,0,0), B(a,0,0) y C(0,a,0).

1. Calcula la posición de equilibrio de la partícula.
2. Considera las situaciones siguientes
   1. m = 0 y k_A = k_B = k_C = k
   2. m = 0 y
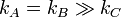
   3. k_A = k_B = k_C = k y m > > ka / g.

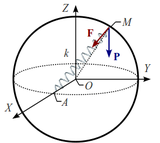
2 Equilibrio de una partícula sobre una esfera lisa

Un punto material M de peso P está obligado a permanecer en la superficie de una esfera de radio R y centro O. Además, M es atraído por un punto fijo A del ecuador de la superficie esférica, debido a la existencia de un resorte elástico ideal, de longitud natural nula y de constante recuperadora 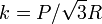, que conecta ambos puntos. Determina las posiciones de equilibrio del punto material M, y la fuerza de reacción vincular en ellas.

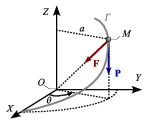
3 Equilibrio de una partícula sobre una hélice

Un punto material M, de peso P, está vinculado a la hélice Γ, definida en el sistema de referencia cartesiano OXYZ por la ecuación vectorial 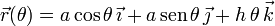. Determina la posición de equilibrio estático del punto M si, además, este es atraído por el origen por una fuerza proporcional a la distancia entre ambos puntos, siendo k la constante de proporcionalidad.

4 Fuerza unidireccional

Una partícula de masa m está sometida a una fuerza constante 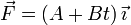. Si parte del reposo y desde el origen del sistema de referencia, encuentra la posición y la velocidad de la partícula en cualquier instante.