Problemas de dinámica de la partícula (GIE)

De Laplace

1 Masa girando alrededor de una mano

Una masa de 0.5 kg situada en el extremo de una cuerda de 50 cm de longitud se hace girar horizontalmente con la mano de manera que da 2 vueltas por segundo. ¿Puede estar la cuerda completamente horizontal? Determine la tensión de la cuerda y el ángulo que forma con la horizontal.

2 Ascenso de una grúa

Una grúa eleva una masa de 500 kg con velocidad vertical constante 0.5 m/s mientras la pluma gira un arco de 90° en 15 s. Si el carro se encuentra a 10 m del mástil, determine la inclinación del cable y la tensión que soporta cuando su longitud es de 5 m.

3 Una masa sobre otra

Sobre una mesa horizontal se encuentran apilados dos bloques, siendo el inferior de masa m₁ y el superior de masa m₂. El coeficiente de rozamiento estático del bloque inferior con la mesa vale μ₁ y el del segundo bloque con el primero μ₂. Los coeficientes de rozamiento dinámico valen lo mismo que los estáticos.

1. Indique la fuerza que la mesa ejerce sobre el bloque inferior y el que éste ejerce sobre el superior.
2. Suponga que se tira del bloque inferior con una fuerza horizontal . ¿Cuánto debe valer como mínimo esta fuerza si se quiere que el bloque superior se quede atrás?
3. Si se aplica una fuerza por encima de este valor mínimo, ¿que fuérzas actúan sobre cada uno de los bloques? ¿Cuál es la aceleración de cada uno?

4 Dos masas, un plano y un hilo

Se tienen dos masas m₁ y m₂ atadas por un hilo ideal sin masa, que pasa por una polea también ideal. La masa m₁ se encuentra sobre un plano inclinado un ángulo α. La masa m₂ cuelga verticalmente.

1. Suponiendo que no hay rozamiento, determine la aceleración de las masas. ¿Cuál debe ser la relación entre ellas para que el sistema se quede en equilibrio?
2. Entre la masa m₁ y el plano existe un coeficiente de rozamiento estático μ. ¿Cuál debe ser el mínimo y el máximo valor de m₂ para que las masas queden en equilibrio?

5 Curvas y peraltes

El circuito de Indianápolis posee curvas de 200m de radio peraltadas un ángulo de 9º12'.

1. Si no se considera el rozamiento, ¿con qué rapidez debe ir un coche si no quiere deslizarse ni hacia arriba ni hacia abajo?
2. El coeficiente de rozamiento lateral de un coche con la pista vale μ = 1.5. ¿Cuáles son las velocidades máximas y mínimas que puede adquirir un coche sin derrapar?

6 Amortiguamiento viscoso

El rozamiento que experimenta una pequeña partícula en medio denso y viscoso como un aceite es de la forma 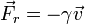. Se construye un sensor de balística, en el que una bala de masa m impacta horizontalmente en un bloque de silicona en el que se cumple la ley anterior. Si la bala recorre una distancia x₀ hasta pararse. ¿Con qué velocidad impactó en el bloque?

7 Doble máquina de Atwood

La doble máquina de Atwood de la figura está formada por tres masas unidas a través de dos cuerdas ideales y dos poleas también ideales. Determine la aceleración de cada una de las masas, así como las tensiones de las dos cuerdas.

8 Ascenso de una grúa

Una grúa sube una masa de 100 kg con velocidad vertical constante de 0.5 m/s mientras la pluma gira un arco de 90° en 15 s, Si el carro se encuentra a 10 m del mástil, determine la inclinación del cable y la tensión que soporta cuando su longitud es de 10 m.

9 Mundo Anillo

En la novela Mundo Anillo de Larry Niven se describe un planeta artificial en forma de un anillo alrededor del Sol, siendo el radio del anillo 1.02 UA y su aceleración tal que produce una gravedad aparente de 0.992g. Determine el periodo orbital del anillo.

Si desde la superficie del Mundo Anillo enfrentada al Sol se lanza una piedra verticalmente hacia arriba, y despreciando el rozamiento con el aire, ¿caerá detrás del punto de lanzamiento (en el sentido de giro), en el mismo punto de lanzamiento, o delante de él?

10 Dos muelles enfrentados

Una partícula de masa m se encuentra situada entre dos resortes de longitudes en reposo l₁₀ y l₂₀, que se encuentran atados a paredes opuestas separadas una distancia L. Los muelles poseen constantes de recuperación k₁ y k₂.

1. Determine la posición de equilibrio de la masa. ¿A cuanto tiende esta posición si 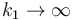? ¿Y si ?
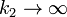2. Estando en la posición de equilibrio, se le comunica a la masa una velocidad v₀. Determine la amplitud y la frecuencia de las oscilaciones resultantes.

11 Partícula cargada en campo magnético uniforme

Una carga q en campo magnético experimenta una fuerza

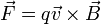
Se trata de deducir cómo se mueve la partícula en el caso en el que el campo magnético sea una constante independiente de la posición.

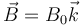
1. Suponga en primer lugar que la velocidad inicial de la partícula es paralela al campo magnético, 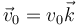. ¿Cuánto vale la aceleración en el instante inicial? ¿Cuanto vale la velocidad un instante posterior? ¿Cómo es el movimiento de la carga en ese caso?
2. Suponga ahora el caso de una carga cuya velocidad inicial es perpendicular al campo magnético, .
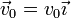   1. Demuestre que el movimiento resultante es un movimiento plano.
   2. Demuestre que la rapidez del movimiento es constante
   3. Calcule el radio de curvatura de la trayectoria que describe la carga
   4. ¿Qué tipo de movimiento describe la partícula?
3. Suponga, por último, una velocidad inicial arbitraria 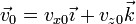. Combinado los resultados anteriores, ¿qué movimiento realiza la carga?

12 Partícula suspendida de resorte e hilo

Una partícula de peso se encuentra atada simultáneamente a una barra rígida de longitud 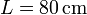y a un muelle de longitud natural nula y constante k desconocida. Los anclajes de la barra y el resorte distan 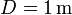. En la posición de equilibrio, la longitud del resorte es .

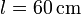1. Determine la tensión de la barra y la constante recuperadora del resorte.
2. Suponga que se corta la unión de la masa con el resorte. ¿Qué movimiento describe la masa a partir de ese momento?
3. Suponga que, en lugar de lo anterior, se corta la unión de la masa con la barra. ¿Qué movimiento describe en ese caso? Calcule la amplitud y frecuencia del movimiento resultante.