Problemas de introducción a la mecánica de fluidos
De Laplace
Contenido |
1 Masa y altura media de la atmósfera
Si el radio de la Tierra es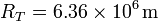 
y la presión atmosférica a nivel del mar es 
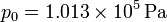, calcule la masa total de la atmósfera, suponiendo que todos sus puntos están sometidos al mismo valor de 
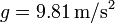. Si la densidad de masa de la atmósfera fuese la del aire a nivel del mar, 
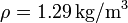, calcule la altura de la atmósfera sobre la superficie de la Tierra.
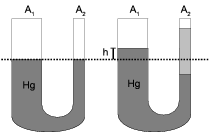
2 Elevación de mercurio en un tubo en U
Se vierte mercurio en un un tubo en U. El brazo izquierdo del tubo tiene una sección transversal de área A1 = 10.0 cm2, y la del brazo derecho es A2 = 5.00 cm2. A continuación se vierten 100 g de agua en el brazo derecho del tubo.
- Determina la altura de la columna de agua en el brazo derecho del tubo relativa a la del mercurio en el izquierdo.
- Si la densidad del mercurio es ρHg = 13.6 g/cm3, ¿qué distancia ascenderá el mercurio en el brazo izquierdo?
3 Presión en el interior del océano
Calcule la presión absoluta a 1000 m de profundidad en el océano. Considere que la densidad del agua es 1024 kg/m³ y que el aire que hay encima ejerce una presión de 101.3 kPa. A esta profundidad, ¿qué fuerza debe ejercer el armazón de la escotilla circular, de radio 30.0 cm, de un submarino para contrarrestar la fuerza del agua?
4 Modelo de atmósfera isoterma
Suponiendo que la densidad del aire en la atmósfera es proporcional a la presión, demuestre que la variación de la presión atmosférica con la altura es P(y) = P0e − αy, siendo g la aceleración de la gravedad y α = ρ0g / P0, con ρ0 y P0 la densidad del aire y la presión atmosférica a nivel del mar (y = 0).
5 Modelo de densímetro
Un modelo sencillo de densímetro consiste en una jeringuilla en cuyo interior hay una barra delgada de longitud L y densidad de masa ρ0 conocida. Se aspira dentro de la jeringuilla una cantidad del líquido del que se quiere medir la densidad ρ, de modo que la barra flota parcialmente en él, sobresaliendo una distancia h. Encuentre la expresión que da la densidad del líquido.
6 Tubo de Venturi
El tubo de Venturi se utiliza para medir la velocidad de un fluido incompresible. Consiste en un tubo con un estrechamiento, de modo que las secciones antes y después del estrechamiento son A1 y A2, con A1 > A2. En cada parte del tubo hay un manómetro, de modo que se pueden medir las presiones respectivas p1 y p2. Encuentra una expresión para la velocidad del fluido en cada parte del tubo en función del área de las secciones, las presiones y su densidad.
7 Diseño de una clepsidra
Una clepsidra es un reloj de agua, usado en tiempos antiguos para medir el tiempo. Un modelo simple consiste en un recipiente abierto al aire en su parte superior, con un agujero de pequeña sección en el fondo. El recipiente se llena de agua y esta fluye por el agujero. La variación del nivel de agua en el recipiente indica el paso del tiempo. Para poder usar una escala equiespaciada es conveniente que la velocidad con que baja el nivel de agua sea constante. Si la forma del recipiente es de un volumen de revolución, de modo que para cada altura su sección es un círculo de radio r(y), y el radio del orificio de salida es r0, encuentra el perfil de la curva que consigue que la velocidad con que desciende el nivel de agua sea constante.
