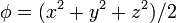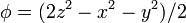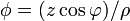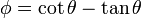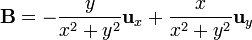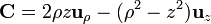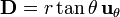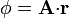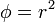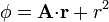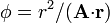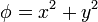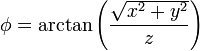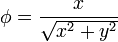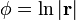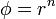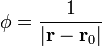Problemas de fundamentos matemáticos
De Laplace
1 Campos escalares en diferentes sistemas
Exprese los siguientes campos escalares en coordenadas cartesianas, cilíndricas y esféricas
2 Campos vectoriales en diferentes sistemas
Exprese los siguientes campos vectoriales en coordenadas cartesianas, cilíndricas y esféricas:
3 Trazado de superficies equiescalares
Describa las superficies equipotenciales de los siguientes campos escalares
donde  es un vector constante y
es un vector constante y  es el vector de posición.
es el vector de posición.
4 Cálculo de gradientes
Para los campos escalares
calcule su gradiente en coordenadas cartesianas, cilíndricas y esféricas.
5 Regla de la cadena para gradientes
Si 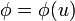 , con
, con 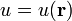 , demuestre que
, demuestre que
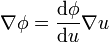
Encuentre 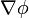 si
si
6 Integral sobre una superficie esférica
Halle el valor de la integral
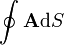
con
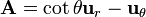
y la superficie de integración una esfera de radio R centrada en el origen.
7 Cálculo de divergencias y rotacionales
Para los campos vectoriales
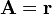
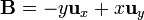
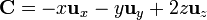
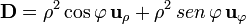 $
$
calcule su divergencia y su rotacional, empleando en cada caso, coordenadas cartesianas, cilíndricas y esféricas. ¿Cuáles son irrotacionales y cuáles solenoidales?
8 Cálculo de flujo
Para el campo vectorial
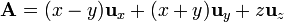
calcule su flujo a través de las siguientes superficies cerradas:
- Un cubo de arista a, con un vértice en el origen y aristas
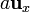 ,
, 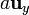 y
y 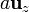 .
.
- Un cilindro circular de altura h y radio R, con el eje Z como eje y sus bases situadas en z = 0 y z = h.
- Una esfera de radio R en torno al origen de coordenadas.
En cada caso, halle el flujo por integración directa y por aplicación del teorema de Gauss.
9 Cálculo de circulación
Para el campo vectorial
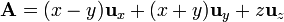
calcule su circulación a lo largo de las siguientes curvas cerradas:
- Un cuadrado de lado 2a, con vértices
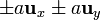 .
.
- Una circunferencia de radio R situada en el plano z = 0 y con centro el origen de coordenadas.
- Una circunferencia vertical, situada en el plano x = y y con centro el origen de coordenadas.
En cada caso, halle la circulación por integración directa y por aplicación del teorema de Stokes.