Órbita de transferencia

De Laplace

Revisión a fecha de 18:21 13 may 2010; Anamaram (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Introducción
2 Órbita de transferencia de Hohmann
3 Velocidad inicial y final
4 Impulso
5 Valores numéricos
6 Ventanas de lanzamiento

1 Introducción

Una órbita de transferencia es aquella que debe seguir un satélite para desplazarse desde una órbita circular de un cierto radio a una de un radio diferente. Por ejemplo, si interesa lanzar un satélite a Marte, dicha nave debe salir desde la órbita terrestre (a 1 UA del Sol) y llegar hasta la órbita marciana (a 1.66 UA). El camino que recorre es la órbita de transferencia.

2 Órbita de transferencia de Hohmann

Podría parecer que lo más sencillo sería lanzar el cohete en línea recta desde la Tierra a Marte, pero eso no tiene en cuenta un factor esencial. Una vez que sale del campo gravitatorio terrestre, la nave no sigue un movimiento rectilíneo y uniforme, sino que sigue sometida a la gravedad solar, por lo que describe un movimiento elíptico, como el resto de los cuerpos del sistema solar.

La órbita que requiere un menor impulso inicial es aquella que hace un mayor uso del movimiento que el Sol imprime a la nave. Esto se consigue con la llamada órbita de transferencia de Hohmann (en honor a Walter Hohmann). En esta órbita se le comunica solamente un impulso inicial a la nave y uno final a la llegada a Marte. Entre estos dos puntos, la nave describe media elipse con el Sol en uno de sus focos, estando uno de los vértices en la posición inicial en la Tierra y el opuesto en la posición final en Marte.

En lo que sigue analizaremos esta órbita, calculando la velocidad inicial que debe comunicarse y la velocidad a la llegada, así como otros parámetros de interés.

3 Velocidad inicial y final

La clave para determinar las velocidades en los puntos iniciales es usar los teoremas de conservación para una partícula. La fuerza gravitatoria es una fuerza central, por lo que conserva el momento cinético del satélite, medido respecto al Sol

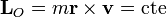
$\mathbf{L}_O=m\mathbf{r}\times\mathbf{v}=\mathrm{cte}\,$

También es una fuerza conservativa, por lo que también se conserva la energía mecánica

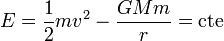
$E=\frac{1}{2}mv^2 - \frac{GMm}{r}=\mathrm{cte}$

Aplicamos estas dos leyes a los puntos inicial y final de la órbita de transferencia. Por tratarse de vértices de la elipse, en los dos la velocidad es perpendicular al vector de posición, por lo que la única componente del momento cinético es

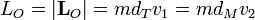
$L_O=\left|\mathbf{L}_O\right|=md_Tv_1 = md_Mv_2\,$

Igualando también las energías mecánicas inicial y final

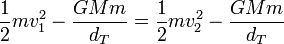
$\frac{1}{2}mv_1^2 -\frac{GMm}{d_T}=\frac{1}{2}mv_2^2 - \frac{GMm}{d_T}$

Esto nos da un sistema de dos ecuaciones con dos incógnitas, que podemos resolver de forma sencilla. De la conservación del momento cinético obtenemos

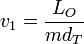
$v_1 = \frac{L_O}{md_T}$ $v_2 = \frac{L_O}{md_M}$

Sustituyendo en la ley de conservación de la energía obtenemos una ecuación para el momento cinético

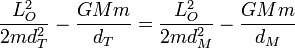
$\frac{L_O^2}{2md_T^2}-\frac{GMm}{d_T}=\frac{L_O^2}{2md_M^2}-\frac{GMm}{d_M}$

Agrupando términos

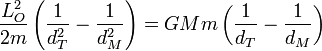
$\frac{L_O^2}{2m}\left(\frac{1}{d_T^2}-\frac{1}{d_M^2}\right) = GMm\left(\frac{1}{d_T}-\frac{1}{d_M}\right)$

Simplificando y despejando

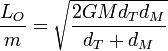
$\frac{L_O}{m}=\sqrt{\frac{2GMd_Td_M}{d_T+d_M}}$

Esto nos da las velocidades inicial y final

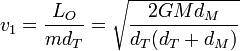
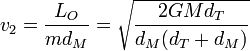
$v_1 = \frac{L_O}{md_T}=\sqrt{\frac{2GMd_M}{d_T(d_T+d_M)}}$ $v_2 = \frac{L_O}{md_M}=\sqrt{\frac{2GMd_T}{d_M(d_T+d_M)}}$

Estas velocidades dependen de la constante $G M$ , igual al producto de la constante de Gravitación Universal por la masa del objeto masivo, el Sol en este ejemplo. Podemos obtener el valor de esta constante, observando que para una órbita circular, como la de la Tierra, la fuerza gravitatoria es puramente normal y por tanto

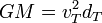
$\frac{v_T^2}{d_T}=\frac{GM}{d_T^2}$ $\Rightarrow$ $GM=v_T^2d_T$

A su vez, la velocidad de la Tierra observando que conocemos la distancia que recorre en un año. Sustituyendo el valor de la constante

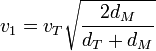
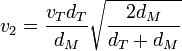
$v_1 = v_T \sqrt{\frac{2d_M}{d_T+d_M}}$ $v_2=\frac{v_Td_T}{d_M}\sqrt{\frac{2d_M}{d_T+d_M}}$

Si llamamos $γ = d M / d T$ a la proporción entre las distancias al Sol, estas expresiones quedan en la forma más sencilla

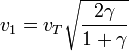
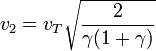
$v_1 = v_T \sqrt{\frac{2\gamma}{1+\gamma}}$ $v_2=v_T\sqrt{\frac{2}{\gamma(1+\gamma)}}$

4 Impulso

El valor de $v 1$ calculado anteriormente representa la velocidad que tiene el satélite al iniciar la órbita de transferencia. Pero esa no es la velocidad que le debemos comunicar al satélite para ponerlo en órbita, ya que el satélite, ya posee la velocidad orbital de la Tierra. por ello, la magnitud que nos interesa es el incremento de velocidad (o, “delta-v”) respecto a la que ya tiene por estar sobre la Tierra

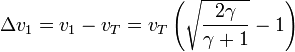
$\Delta v_1 = v_1 - v_T = v_T\left(\sqrt{\frac{2\gamma}{\gamma+1}}-1\right)$

Esta es la velocidad, vista desde la Tierra, con la que el satélite debe iniciar la órbita.

Del mismo modo, al llegar a Marte, debe igualmente adaptarse a la velocidad orbital marciana. Podemos obtener esta velocidad observando que puesto que $G M$ es el mismo para ambos planetas, se cumple la llamada tercera ley de Kepler

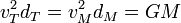
$v_T^2d_T = v_M^2d_M = GM$

de donde

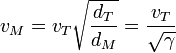
$v_M = v_T\sqrt{\frac{d_T}{d_M}}= \frac{v_T}{\sqrt{\gamma}}$

por lo que el delta-v a la llegada es

$\Delta v_2 = v_M-v_2 = \frac{v_T}{\sqrt{\gamma}}\left(1-\sqrt{\frac{2}{1+\gamma}}\right)$

El incremento $Δ v 1$ es la velocidad con la que la nave debe salir de la atracción terrestre, pero no aquella con la que debe lanzarse la nave. Debemos tener en cuenta además el fenómeno de la velocidad de escape. Si nos imaginamos un único impulso inicial (un cañonazo como en “De la Tierra a la Luna”), podríamos calcular la velocidad de despegue aplicando de nuevo la conservación de la energía, pero ahora con el campo gravitatorio terrestre.

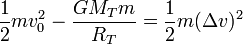
$\frac{1}{2}mv_0^2 - \frac{GM_Tm}{R_T} = \frac{1}{2}m(\Delta v)^2$

de donde

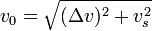
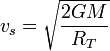
$v_0 = \sqrt{(\Delta v)^2 + v_s^2}$ $v_s = \sqrt{\frac{2GM}{R_T}}$

En realidad, lo que se hace es que la nave se impulsa gradualmente varias fases de combustible.

5 Valores numéricos

Podemos calcular tanto las velocidades inicial y final, como los incrementos a la salida y a la llegada, sustituyendo valores astronómicos.

La velocidad lineal de la tierra es igual a la circunferencia de la órbita, dividida por el periodo orbital (un año). La distancia orbital es 1 UA = 150 millones de kilómetros. Para el periodo, usamos la aproximación

1 año∼10⁷π s

lo que nos da

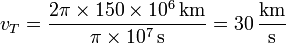
$v_T = \frac{2\pi\times 150\times 10^6\,\mathrm{km}}{\pi\times 10^{7}\,\mathrm{s}}=30\,\frac{\mathrm{km}}{\mathrm{s}}$

El valor exacto de la velocidad orbital promedio es muy próximo: 29.783 km/s.

El radio de la órbita marciana es 1.523 UA lo que nos da una relación entre distancias

$\gamma = \frac{d_M}{d_T}=1.523$

y una velocidad inicial y final

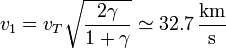
$v_1 = v_T \sqrt{\frac{2\gamma}{1+\gamma}} \simeq 32.7\,\frac{\mathrm{km}}{\mathrm{s}}$

El delta-v que debe comunicársele en la salida es solamente

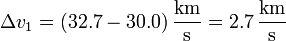
$\Delta v_1 = (32.7-30.0)\,\frac{\mathrm{km}}{\mathrm{s}}=2.7\,\frac{\mathrm{km}}{\mathrm{s}}$

A la llegada, la velocidad en la órbita de transferencia es

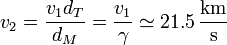
$v_2 = \frac{v_1d_T}{d_M}=\frac{v_1}{\gamma}\simeq 21.5\,\frac{\mathrm{km}}{\mathrm{s}}$

mientras que la velocidad orbital de Marte es

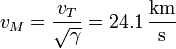
$v_M = \frac{v_T}{\sqrt{\gamma}}=24.1\,\frac{\mathrm{km}}{\mathrm{s}}$

lo que implica un incremento de velocidad a la llegada de 2.6 km/s.

6 Ventanas de lanzamiento

Para que la órbita de transferencia de Hohmann funcione, tanto la Tierra como Marte deben encontrarse en los extremos de la elipse, por lo que el satélite no puede lanzarse en el momento en que a uno más le apetezca. La fecha de lanzamiento ha de ser tal que, para cuando el satélite llegue a la órbita marciana, Marte se encuentre allí, y no en otro punto de la órbita.

La duración de la órbita de transferencia es la mitad del periodo orbital en la órbita de transferencia. Este periodo se obtiene aplicando la tercera ley de Kepler (“los cuadrados de los periodos son proporcionales a los cubos de los semiejes mayores”), que se deduce de la conservación de la energía y del momento cinético. Aplicando esta relación a la nave y a la propia Tierra

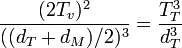
$\frac{(2T_v)^2}{((d_T+d_M)/2)^3} = \frac{T_T^3}{d_T^3}$

Despejando de aquí resulta el tiempo de viaje

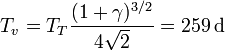
$T_v = T_T \frac{(1+\gamma)^{3/2}}{4\sqrt{2}}=259\,\mathrm{d}$

Por tanto, la nave debe ser lanzada 259 días antes de que Marte llegue al punto opuesto del punto de lanzamiento. Un año marciano dura, por la misma ley de Kepler

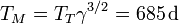
$T_M = T_T \gamma^{3/2} = 685\,\mathrm{d}$

por lo que la nave debe ser lanzada cuando los vectores de posición de la Tierra y Marte forman un ángulo

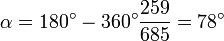
$\alpha = 180^\circ - 360^\circ\frac{259}{685} = 78^\circ$

Para esta posición existe una pequeña ventana de unos cuantos días en la que es posible realizar el lanzamiento.

¿Cada cuanto tiempo se produce esta ventana?

Desde un sistema ligado a la Tierra ("0") la velocidad angular de Marte ("2") alrededor del Sol ("1") es

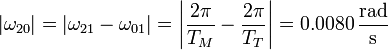
$|\omega_{20}|=|\omega_{21}-\omega_{01}| = \left|\frac{2\pi}{T_M}-\frac{2\pi}{T_T}\right|=0.0080\,\frac{\mathrm{rad}}{\mathrm{s}}$

Esto quiere decir que Marte vuelve a estar en la misma posición respecto a la tierra cada

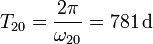
$T_{20}=\frac{2\pi}{\omega_{20}}=781\,\mathrm{d}$

o, lo que es lo mismo, cada 2.1 años. Esto quiere decir que si el lanzamiento se ve frustrado (por mal tiempo u otros problemas) hay que esperar más de dos años para volverlo a intentar.

Órbita de transferencia

De Laplace

Contenido

1 Introducción

2 Órbita de transferencia de Hohmann

3 Velocidad inicial y final

4 Impulso

5 Valores numéricos

6 Ventanas de lanzamiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES